Hrvatski matematički elektronski časopis math.e

13. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE

Trogir, 5. - 8. svibnja 2004.

Zadaci za III. razred


  1. Neka je ABCD kvadrat i P točka na kružnici opisanoj kvadratu na luku AB koji ne sadrži točku C. Koje vrijednosti može poprimiti izraz

    (|AP| + |BP|) / (|CP| + |DP|) ?

  2. Dokažite da u svakom trokutu vrijedi nejednakost

    cos(alfa)/a^3+...>=3/2abc

    pri čemu su a, b, c duljine stranica, te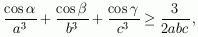 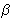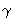alfa, beta, gama odgovarajući kutovi.

  3. Visine trostrane piramide sijeku se u jednoj točki. Dokažite da ta točka, težište jedne strane piramide, nožište visine na tu stranu i tri točke koje dijele preostale tri visine u omjeru 2 : 1, počevši od vrha piramide, leže na istoj sferi.

  4. Konačan broj polja beskonačne kvadratne mreže obojen je crnom bojom. Dokažite da je u toj ravnini moguće odabrati konačno mnogo kvadrata koji zadovoljavaju svaki od sljedećih uvjeta:
        (i)   Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).
        (ii)   Svako crno polje leži u nekom od tih kvadrata.
        (iii)   Površina crnih polja u svakom od odabranih kvadrata je barem 1/5, a najviše 4/5 površine tog kvadrata.