Hrvatski matematički elektronski časopis math.e
	http://web.math.hr/mathe/

12. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE

Pula, 7. - 10. svibnja 2003.

Zadaci za IV. razred

1. Neka je I točka na simetrali kuta BAC trokuta ABC, a M i N redom točke na stranicama AB i AC, takve da je ABI = NIC i ACI = MIB.
   Dokažite da je I središte upisane kružnice trokuta ABC ako i samo ako su točke M, N i I kolinearne.

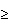2. Niz realnih brojeva (a_n)_{n 0} ima svojstvo da za sve m 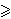n 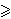0 vrijedi

   a_m+n + a_m-n = (a_2m + a_2n) / 2.

   Odredite a₂₀₀₃ ako je a₁ = 1.

3. Prirodni brojevi od 1 do 2003 poredani su u niz. Na nizu vršimo ovu operaciju: ako je prvi broj u nizu jednak k, okrenemo poredak prvih k brojeva. Dokazati da se nakon konačno uzastopnih primjena ove operacije broj 1 pojavi na prvom mjestu, nezavisno od početnog rasporeda.

4. Dokažite da je

   

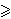   djeljivo s p, za svaki prost broj p i svaki prirodan broj n p.