


44. MEĐUNARODNA MATEMATIČKA OLIMPIJADA
Tokyo, Japan, 7. - 17. srpnja 2003.
Zadaci
- Neka je A podskup skupa S =
{1, 2, ... , 1000000} koji sadrži točno 101 element.
Dokazati da postoje brojevi t1,
t2, ... , t100
u S takvi da su skupovi
Aj = {x + tj | x
u parovima disjunktni.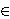 A} za j = 1, 2, ... , 100
A} za j = 1, 2, ... , 100 - Odrediti sve parove (a, b) pozitivnih cijelih
brojeva, takve da je
a2 / (2ab2 - b3 + 1)
pozitivan cijeli broj. - Dan je konveksan šesterokut kod kojeg svake dvije
nasuprotne stranice imaju ovo svojstvo: udaljenost njihovih
polovišta jednaka je produktu broja
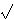 3 / 2
i zbroja njihovih duljina. Dokazati da su svi kutovi
šesterokuta mađusobno jednaki.
3 / 2
i zbroja njihovih duljina. Dokazati da su svi kutovi
šesterokuta mađusobno jednaki.
(Konveksan šesterokut ABCDEF ima tri para nasuprotnih stranica: |AB| i |DE|, |BC| i |EF|, |CD| i |FA|.) - Neka je ABCD tetivni četverokut. neka su P, Q i R nožišta okomica
iz točke D na pravce BC, CA i AB, tim redom. Dokazati da je
|PQ| = |QR| ako i samo ako se simetrale kutova
 ABC i
ABC i
 ADC
sijeku u točki koja leži na pravcu AC.
ADC
sijeku u točki koja leži na pravcu AC.
- Neka je n pozitivan cijeli broj i
x1, x2, ... ,
xn realni brojevi, takvi da je
x1
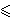 x2
x2 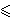 ...
... 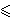 xn.
xn.
(a) Dokazati nejednakost
(b) Pokazati da jednakost vrijedi ako i samo ako je x1, ... , xn aritmetički niz.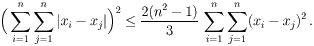
- Neka je p prost broj. Dokazati da postoji prost broj q takav da za svaki cijeli broj n, broj np - p nije djeljiv s q.
