


6. MEDITERANSKO MATEMATIČKO NATJECANJE
Zagreb, 12. travnja 2003.
Zadaci
- Dokažite da jednadžba
x2 + y2 + z2 = x + y + z + 1
nema rješenja u skupu racionalnih brojeva. - Dan je trokut ABC u kojem je
|BC| = |CA| + |AB| / 2.
Točka P je na stranici AB takva da je|BP| / |PA| = 1 / 3.
Dokažite da je CAP
= 2
CAP
= 2  CPA.
CPA.
- Neka je a, b, c
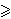 0,
a + b + c = 3. Dokažite nejednakost
0,
a + b + c = 3. Dokažite nejednakost
a / (b2+1) + b / (c2+1) + c / (a2+1)
Kada vrijedi jednakost?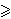 3 / 2.
3 / 2.
- Promatrajte sistem od beskonačno mnogo metalnih sfera,
čija su središta u točkama (a,b,c)
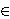
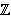
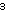 . Kažemo da je sistem stabilan ako je temperatura
svake sfere jednaka srednjoj vrijednosti temperatura šest njoj
najbližih sfera.
. Kažemo da je sistem stabilan ako je temperatura
svake sfere jednaka srednjoj vrijednosti temperatura šest njoj
najbližih sfera.
Uz pretpostavku da je temperatura svake sfere između 0o C i 1o C, te da je sistem stabilan, dokažite da sve sfere moraju imati jednaku temperaturu.
