11. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE

Zadar, 2. - 5. svibnja 2002.

Zadaci za I. razred

1. Duljina srednjice trapeza je 4, a kutovi uz jednu osnovicu su 40^o i 50^o. Odredite duljine osnovica ako je udaljenost njihovih polovišta jednaka 1.

2. Dokažite da za bilo koje pozitivne brojeve a, b, c i bilo koji nenegativan cijeli broj p vrijedi nejednakost

   a^p+2 + b^p+2 + c^p+2 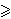a^pbc + b^pca + c^pab.

3. Nađite sve trojke (x,y,z) prirodnih brojeva koji zadovoljavaju jednadžbu

   2x²y² + 2y²z² + 2z²x² - x⁴ - y⁴ - z⁴ = 576.

4. "Kolo sreće" podijeljeno je na 30 odjeljaka u koje su upisani brojevi 50, 100, 150, ... , 1500 (u nekom redosljedu). Dokažite da postoje tri uzastopna odjeljka u kojima je zbroj brojeva veći ili jednak 2350.