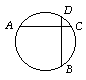11. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Zadar, 2. - 5. svibnja 2002.
Zadaci za VIII. razred
- Odredi sve parove realnih brojeva (x,y) takve da je
x - 12y = 4 i 2x - 24y = 8xy.
- U kutiji se nalaze kuglice i kockice crvene i zelene boje, pri
čemu kuglice čine 48% ukupnog broja predmeta u kutiji. Omjer broja
crvenih kuglica i broja zelenih kuglica jednak je omjeru broja
svih crvenih predmeta i broja svih zelenih predmeta u kutiji.
Izračunaj omjer broja crvenih kuglica i broja crvenih kockica
u kutiji.
- Radnik je neki posao završio za 5 dana. Prvog dana je obavio
1/m posla, gdje je m neki prirodni broj. Drugog
dana obavio je 1/n ostatka posla koji mu je ostao nakon
prvog dana, pri čemu je n neki prirodni broj veći od m.
Trećeg dana radnik je obavio 1/m ostatka posla koji mu je
ostao nakon drugog dana, a četvrtog dana još 1/n posla
preostalog nakon trećeg dana. Petog dana je obavio preostalu
1/4 cijelog posla. Odredi brojeve m i n.
- Dan je pravokutni trokut ABC takav da je
 BCA =
90o i
BCA =
90o i
 CAB =
15o. Izračunaj vrijednost izraza
AC /
BC +
BC /
AC.
CAB =
15o. Izračunaj vrijednost izraza
AC /
BC +
BC /
AC.
- Dužine AC i
BD dvije su
međusobno okomite tetive kružnice, kao na slici. Okomica povučena iz
točke A na pravac CD siječe pravac BD u točki M, a okomica
iz točke B na pravac CD siječe pravac AC u točki N. Dokaži da je
četverokut ABNM romb.