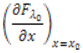| Logističko preslikavanje |
 |
 |
|
Sadržaj: 1. UvodProučavanjem ljudske povijesti lako se dolazi do zaključka da je u ljudsku prirodu ugrađen nagon za proučavanjem, shvaćanjem i kontroliranjem svijeta oko sebe. Kroz iskustvo koje čovječanstvo prenosi s generacije na generaciju, naučili smo da je prvi korak do rješenja mnogih problema njihovo teorijsko razmatranje i rješavanje na toj razini. Nakon toga možemo se odvažiti na rješavanje u stvarnom svijetu. Problemi su manje ili više komplicirani, pa pokušavamo za svaki od njih stvoriti model koji ih opisuje što bolje i to u uvjetima koje mi kontroliramo. Iako se neki od problema s kojima se susrećemo mogu riješiti bez previše teoretiziranja, za rješavanje drugih problema potrebno je imati plan i program koji često svoj oblik nalazi u jeziku matematike. Svijet u kojem se nalazimo sustav je akcije i reakcije, povratnih veza, međusobnih utjecaja i poticaja. Iz tog razloga, kako bismo mogli objasniti pojave iz svojeg okoliša, morali smo smisliti alat koji ih opisuje "na papiru". Diferencijalne i diferencijske jednadžbe dva su alata koji su se pokazali iznimno učinkovitim u rješavanju dinamičkih problema kao u teoriji, tako i u praksi. U ovom radu proučavat ćemo samo jedan mali dio teorijskog baratanja i određivanja karakteristika jednadžbi koje opisuju pojave kao što su rast populacije, dohotka na bankovnom računu ili numeričko izračunavanje korijena jednadžbi. Točnije, ono čime će se većina ovog rada baviti je logističko preslikavanje (logistička, populacijska jednadžba) i karakteristike koje ono donosi sa sobom, te kako se njihovo teorijsko razmatranje može lagano preslikati u stvarni svijet i pojavu koju ono opisuje. Jedno od karakterističnih svojstava logističkog preslikavanja je pojava determinističkog kaosa koji dolazi do izražaja za određene vrijedosti parametara svojstvenih za samo preslikavanje. Budući da je deterministički kaos zanimljivo područje za proučavanje, u ovome radu pozabavit ćemo se i teorijskim promatranjem specifičnih situacija, pa ćemo tako odgovoriti na pitanja zašto i kada kaos dolazi do izražaja. Treba spomenuti i ime američkog matemaričara M. Feigenbauma koji je među prvima počeo s proučavanjem teorije kaosa i čijom su zaslugom otkriveni matematički pojmovi kao što su Feigenbaumove konstante koje ćemo nešto detaljnije pojasniti u samom radu. 2. Uvod u logističku jednadžbuKako bismo mogli u potpunosti razumjeti složeno ponašanje logističke jednadžbe, moramo krenuti od jednostavnijih primjera te postupno napredovati. U tom duhu, krenimo od jednog vrlo jednostavnog primjera diskretnog dinamičkog sustava koji opisuje godišnje ukamaćivanje određene svote u banci za kamatnu stopu iznosa p. Zbog lakšeg čitanja i kasnije primjene, označimo iznos nakon n-te godine s An. Tako će A0 biti početni iznos, a A1 iznos nakon prve godine i on će iznositi Odnosno, općenito pa, prema tome, iznos A2 je Daljnjim primjenjivanjem postupka lako se dolazi do Ovakvim pristupom uspješno smo riješili problem nepotrebnog uvrštavanja prethodnih n rezultata u svrhu izračunavanja An. Oblik dobivene jednadžbe naziva se eksponencijalnom jednadžbom. Možemo primijetiti kako izraz opisuje An samo u ovisnosti o n, vrijednosti p i početnoj vrijednosti A0, te taj izraz smatramo rješenjem jednadžbe. Oblik rješenja koje ovisi samo o poznatim vrijednostima i varijablama nazivamo zatvorenim oblikom, no treba napomenuti kako je broj rekurzivnih jednadžbi koje se mogu eksplicitno riješiti malen. Kao što smo već primjetili, An ovisi o p koji nazivamo parametrom te jednadžbe. Izučavanjem ovog parametra možemo odrediti neke karakteristike sustava koji ona opisuje. U ovisnosti o parametru p i primjenom nekih osnovnih karakteristika eksponencijalne jednadžbe, moguće je doći do sljedećih rezultata:
Slučaj kada je p ∈ (−∞, −1) poseban je slučaj koji zahtijeva posebno razmatranje. Ovdje ga nećemo komentirati, što i nije toliki nedostatak, budući da njegov smisao i ne postoji u opisu početnog problema. Ono što smo uspjeli shvatiti iz razmatranja ostalih triju slučajeva je sljedeće: ako je kamatna stopa negativna, oročeni iznos postupno će nam nestajati, ako je nepostojeća, iznos se neće mijenjati, a ako je pozitivna, ukupni iznos iz godine u godinu će rasti. Pokušajmo sada riješiti sljedeći problem: problem broja populacije određene vrste na nekom zatvorenom području. Prvi pokušaj rješavanja ovog problema izišao je iz pretpostavke da se populacija mijenja proporcionalno njenom iznosu u bilo kojem trenutku. Naravno, ovo je vrlo loša pretpostavka, u što ćemo se i sami moći uvjeriti daljnjim računom. Navedena pretpostavka prevedena u jezik matematike glasi
ili u diskretnom obliku, Primjenom istog postupka kao u prethodnom primjeru dolazimo do gdje je P0 početni broj jedinki, a λ konstanta proporcionalnosti. Glavni nedostatak ove jednadžbe je što je sudbina populacije koju proučavamo određena isključivo parametrom λ. Ako je 0 < λ < 1, populacija je osuđena na propast, a ako je λ >1 populacija će rasti u beskonačnost. Budući da je to nerealna situacija, jer bi u jednom trenu, zbog prenapučenosti, zalihe hrane nestale, te bi populacija bila ponovno (no ovaj put ne u skladu s jednadžbom) osuđena na izumiranje, ovaj model rasta populacije mijenja se u
Razlog ove izmjene nalazimo u sljedećem svojstvu. Ako je P(t) > L, tada smatramo da je populacija premašila granicu ispod koje ta količina jedinki može normalno egzistirati, te ona počinje opadati. S druge strane, ako je P(t) < L, smatramo da je populacija ispod granice (da postoji još mjesta za nove jedinke) te da raste. Ovime smo riješili problem prenapučenosti ili bezrazložnog izumiranja. Kako bismo lakše baratali ovom jednadžbom, postavimo L = 1 te prijeđimo u diskretnu domenu. Možemo pretpostaviti da postavljanjem L = 1 više ne govorimo o broju jedinki u populaciji, već o postotku početne populacije P0. Rezultat koji dobivamo jest upravo logistička jednadžba 3. Iteracijski procesKao što smo vidjeli u prethodnom poglavlju, iznos An ovisi o prijašnjoj vrijednosti An−1. Postupak uvrštavanja prethodne vrijednosti koji smo upotrebljavali kako bismo dobili zatvoreni oblik od An i Pn naziva se iteracijom. No, da bismo lakše radili s takvim funkcijama, uvodimo drukčiji zapis. Pogledajmo konkretni slučaj logističke jednadžbe. Ako zamijenimo xn s x, možemo reći da je lijeva strana jednakosti funkcija od x, ili kraće zapisano Fλ(x) je funkcija koja generira rekurzivnu logističku jednadžbu. Općenito, ponašanje diferencijskih jednadžbi proučavat ćemo korištenjem diferencijalnog računa. No, prije toga, definirajmo notaciju za proces iteracije. Počnimo od početka i označimo početni iznos s x0, zbog čega bi prvi korak iteracije iznosio F(x0), drugi F(F(x0)) i tako dalje. Isto možemo napisati i s pomoću kompozicije funkcija, gdje onda prvi korak ostaje nepromijenjen, no drugi prelazi u F◦F(x0). Generalno, ovaj zapis za n-ti korak jednak je (gdje se F javlja n puta) ili kraće zapisano Ovaj se zapis ne smije zamijeniti potencijom funkcije F na n-tu, no budući da funkcije čije karakteristike istražujemo nećemo potencirati, zapis je sasvim opravdan i jednoznačan u daljnjem tekstu. Tako će sljedeći iteracijski koraci logističke jednadžbe biti jednaki i Uzastopnim iteriranjem ove, ali i drugih diferencijskih jednadžbi, možemo doći do zaključka da za određene funkcije, njene parametre i broj iteracija, iznos n-te iteracije teži ka određenoj vrijednosti. Vrijednost u koju teži naziva se fiksnom točkom. Pojedine karakteristike i tipove fiksnih točaka pobliže ćemo objasniti u sljedećem odlomku, no prije toga uvodimo notaciju za izraz "funkcija F s početnom vrijednošću x0 teži u x∞ kad n teži u beskonačnost". Ovaj tip izraza pisat ćemo kao 4. Fiksne točkeKao što smo spomenuli na završetku prethodnog poglavlja, diferencijske funkcije mogu imati točke koje nazivamo fiksnim točkama. U daljnjoj razradi ove teme, vidjet ćemo kako nisu sve fiksne točke jednake. Tako one mogu biti privlačne, odbojne ili u posebnim slučajevima neutralne. Promotrimo primjer funkcije koja generira logističku jednadžbu: Daljnjim iteracijama rezultat se ne mijenja, pa možemo reći da smo izračunali x∞ u ovom slučaju. Ipak, mora se napomenuti da ovim postupkom nismo egzaktno izračunali vrijednost x∞ jer bi za to bilo potrebno beskonačno mnogo puta iterirati funkciju. Kalkulator koji smo upotrijebili zaokružuje rezultat na određen broj znamenaka, pa se čini da smo dobili egzaktnu vrijednost fiksne točke. Deduktivnim zaključivanjem mogli bismo zaključiti da zaista vrijedi Logično pitanje koje se nameće jest sljedeće: možemo li teorijskim razmatranjem funkcije Fλ(x) odrediti fiksne točke i uvjete pod kojima će n-ta iteracija u njih težiti? Kako bismo našli odgovor na ovo pitanje, pokušajmo prvo predočiti što iteriranje funkcije zapravo znači. Recimo da počinjemo od točke s koordinatama (x0, x0) u ravnini u kojoj je nacrtan graf funkcije Fλ(x). Prvo što radimo jest izračunavanje Fλ(x0), što izgleda kao premještanje u točku na grafu s koordinatama (x0, Fλ(x0)). Nakon toga vraćamo se u točku jednakih koordinata (Fλ(x0), Fλ(x0)) i ponavljamo taj postupak n puta. Grafički to izgleda ovako: 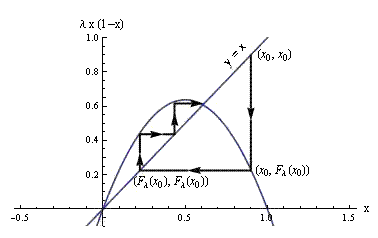 Niz Fλn(x0) prikazan je na pravcu y = x, a na slici 1 prikazan je slučaj kod kojeg niz konvergira u fiksnu točku funkcije Fλ(x). Iz ovakvog predočivanja mogli bismo zaključiti da je dovoljno pronaći rješenja jednadžbe F(x) = x i ta rješenja shvatiti kao fiksne točke funkcije F. Pokušamo li to napraviti za našu funkciju Fλ(x), dobivamo Ovim postupkom našli smo dvije fiksne točke. Primijetimo da vrijednost konačnog rezultata ne ovisi o početnoj vrijednosti. Naravno, ova je tvrdnja točna u slučaju da smo odabrali povoljnu početnu vrijednost koja vodi do konvergencije, pa u toj mjeri izbor početne vrijednosti ipak utječe na krajnji ishod. Ovaj rezultat možemo pokušati iskoristiti za provjeru računa s početka poglavlja. Naime, tamo smo imali λ = 1.5, prema čemu bi vrijedilo sljedeće što je rezultat koji smo i očekivali. Ipak, postoje slučajevi kod kojih rješenja jednadžbe F(x) = x nisu točke kojima će težiti niz Fλn(x0). Pogledajmo račun za &lambda = 1 + √5 i x0 = 1/2: Nije teško primijetiti da se daljnjom iteracijom situacija ne mijenja, već da za bilo koji n ∈ N vrijedi Suprotno tomu, rješavajući jednadžbu F(x) = x mogli bismo pogrešno zaključiti da |Fn1+√5(1/2)| → (1 + √5) / 4. Točke 1/2 i (1 + √5) / 4 nazivaju se periodičkim točkama i one nas uvode u novi pojam koji treba razjasniti, pojam orbita. 5. OrbiteKao što smo već primijetili, rezultati koje dobivamo iteracijom Fλ(x) ovise o parametru λ i o početnoj vrijednosti x0. Kako bismo dobivene rezultate mogli sortirati prema njihovim karakteristikama, uvodimo pojam orbita koji se opisuje na sljedeći način:
(5.1) Orbita U skladu s (5.1) možemo razmatrati nekoliko vrsta orbita čije ćemo karakteristike odmah iznijeti:
(5.2) Fiksna orbita tada je x0 fiksna točka, njezina orbita je konstantna i ima izgled x0, x0, x0, x0…
(5.3) Periodička orbita (ciklus) tada je x0 periodička točka, a najmanji n za koji to vrijedi naziva se osnovnim periodom orbite. Periodička orbita ima izgled uzastopnog ponavljanja niza brojeva Također, kažemo da točke x0, F(x0), …, Fn−1(x0) tvore n-ciklus.
(5.4) S vremenom periodička orbita
U prvom će slučaju x0 biti s vremenom fiksna, a u drugom slučaju s vremenom periodička točka.
(5.5) Orbita koja teži u određenu vrijednost
(5.6) Kaotična orbita 6. Privlačne, odbojne i neutralne točkeU četvrtom poglavlju ustvrdili smo da Fλ(x) ima fiksne točke x0 = 0 i xλ = 1 − 1/λ. No, iako smo dobili ove dvije točke na identičan način, one se razlikuju u svojoj ulozi kod iteriranja same funkcije. Naime, za određene vrijednosti parametra točka xλ ima sposobnost privlačenja, dok x0 ima svojstvo odbijanja. Vizualno to možemo predočiti na sljedeći način:
Na slici 1 prikazan je slučaj privlačne fiksne točke. Ove točke nazivaju se zajedničkim imenom hiperboličke točke, no osim njih postoje i nehiperboličke točke koje nisu niti striktno odbojne niti privlačne.
Ako je x0 fiksna točka od F i ako vrijedi |F'(x0)| < 1, tada točka x0 ima svojstvo privlačenja. Objasnit ćemo ovu tvrdnju koristeći se Lagrangeovim teoremom o srednjoj vrijednosti.
Budući da vrijedi |F'(x0)| < 1, postoji takav broj μ > 0 da vrijedi |F'(x0)| < μ < 1. Nadalje, možemo izabrati broj δ > 0 takav da za bilo koji x ∈ I = [x0 − δ, x0 + δ] vrijedi |F'(x)| < μ < 1. Sada, neka je p ∈ I, p ≠ x0. Primjenom Lagrangeova teorema za funkciju F na intervalu [x0, p] (odnosno [p, x0]) dobivamo:
odnosno Budući da je x0 fiksna točka, vrijedi Iz ove nejednakosti možemo zaključiti da je udaljenost od F(p) do x0 manja od udaljenosti od p do x0, budući da je 0 < μ < 1. To znači da F(p) također leži u intervalu I. Zamjenom p → F(p) dobiva se nejednakost Kako je μ2 < μ (zbog 0 < μ < 1), točke F2(p) i x0 međusobno su bliže nego što su to F(p) i x0. Daljnjim ponavljanjem istog postupka lako se dolazi do Budući da je limn→∞μn = 0, zaključujemo da |Fn(p)| → x0, i to eksponencijalnom brzinom. Na sličan način moguće je pokazati da uz uvjet |F'(x0)| < 1 točka x0 ima svojstvo odbijanja. Primijenimo prethodne zaključke i razmotrimo pod kojim su uvjetima fiksne točke x0 = 0 i xλ = 1 − 1/λ logističkog preslikavanja Fλ(x) = λx(1 − x) privlačne, odnosno odbojne: Fλ'(x0) = Fλ'(0) = λ, Fλ'(xλ) = Fλ'(1 − 1/λ) = 2 − λ. Rezultat koji smo dobili kaže sljedeće. Ako je λ ∈ (−1, 1), tada je točka x0 privlačna, ako je λ = ±1 tada je točka x0 neutralna, a ako je λ < −1 ili λ > 1, točka x0 je odbojna. Istodobno, ako je λ ∈ (1, 3), tada je xλ privlačna, odnosno odbojna ili neutralna ako je λ izvan tog intervala. 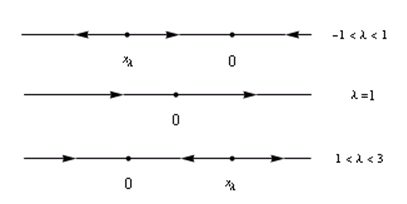
7. Periodičke točkeKao i kod fiksnih točaka, periodičke točke mogu biti klasificirane kao privlačne, odbojne ili neutralne. Način na koji pronalazimo i razmatramo karakteristike takvih točaka pojasnit ćemo u ovom poglavlju. Za početak, moramo naći postupak kojim možemo utvrditi koje su točke potencijalno periodičke. Taj postupak sastoji se od promatranja F2(x) i njezinih fiksnih točaka koje tada predstavljaju periodičke točke kod iteracija F(x). Analogno promatramo F3(x) da bismo pronašli 3-periodičke točke. Kako bismo razjasnili tu tvrdnju, pokažimo najprije grafički prikaz iteriranja 2-ciklusa i 3-ciklusa: 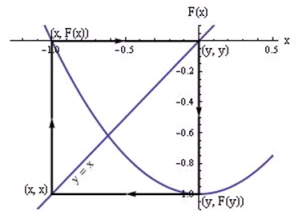
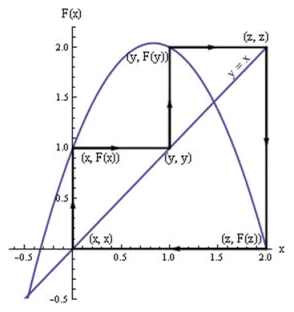
Pokušajmo pronaći jednu od točaka x ili y iz slike 2: F(y) = x = F(F(x)) = F2(x). Odnosno, iz druge slike možemo zaključiti: F(y) = z = F(F(x)) F(z) = x = F(F(F(x))) = F3(x). Dakle, ako tražimo točke funkcije koje čine n-ciklus, tada moramo riješiti jednadžbu Također, valja primijetiti da za fiksnu točku vrijedi Pogledajmo situaciju za konkretan slučaj logističke funkcije: Budući da već znamo kako vrijedi Fλ2(x0) = x0 i Fλ2(xλ) = xλ, možemo ovaj problem svesti na promatranje jednostavnije jednadžbe dijeljenjem Fλ2(x) − x s (x − x0)(x − xλ), nakon čega dobivamo Rješenja ove jednadžbe su
Budući da izraz pod korijenom mora biti veći ili jednak nuli, možemo zaključiti da će Fλ(x) imati 2-periodičke točke ako je njezin parametar unutar skupa (−∞, −1] ∪ [3, +∞). No, što možemo zaključiti o privlačnosti ili odbojnosti ovog 2-ciklusa? Zamijetimo da su točke xp− i xp+ fiksne točke Fλ2(x), u koje bi iteriranjem ove jednadžbe (uz uvjet da je početna vrijednost u blizini jedne od njih) niz težio. Gledajući ove točke iz aspekta iteriranja Fλ(x), one čine 2-ciklus sa svojstvom privlačnosti ili odbojnosti identičnim onome koje posjeduju kao fiksne točke od Fλ2(x). Tako možemo jednostavnom provjerom |(Fλ2(xp−))'| < 1, odnosno |(Fλ2(xp+))'| < 1, odrediti uvjet pod kojim je taj 2-ciklus privlačan. Uvrštavajući jedno od rješenja xp−, xp+ u derivaciju funkcije Fλ2(x), dobiva se Rješavajući nejednadžbu |4 + 2λ − λ2| < 1 dobivamo skup (1 − √6, −1) ∪ (3, 1 + √6). Taj skup sadržava parametre za koje je dobiveni 2-ciklus privlačan. Mi ćemo izbaciti vrijednosti parametra λ < 0 iz okvira našeg promatranja zato što se zanimljivo ponašanje očituje samo za pozitivne vrijednosti parametra. U tom slučaju Fλ(x) spada u klasu unimodalnih preslikavanja koja sva iskazuju kaotično ponašanje na sličan način. Još jedno takvo preslikavanje je f(x) = sin(πx), x ∈ [0, 1], a karakteristika koju dijele sva preslikavanja ovog tipa je graf sljedećeg oblika: 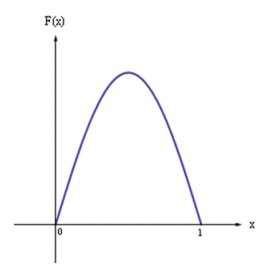
No, možemo li na lakši način provjeriti svojstvo koje ima neki n-ciklus, ako znamo točke koje leže na njemu? Odgovor je da! Problem koji imamo jest izračunavanje (Fn(x))', no budući da je Fn(x) kompozicija n funkcija F(x), primjenom pravila za deriviranje složene funkcije dolazimo do gdje su xn−1, … x0 točke n-ciklusa. Primijetimo još i da vrijedi zato što se točke xn−1, …, x0 periodički ponavljaju i nije bitno kojim redoslijedom množimo F'(xi). Jedan takav primjer možemo vidjeti na kraju 4. poglavlja, gdje je &lambda = 1 + √5, a x0 = 1/2. Kako je F'1+√5(x) = λ(1 &minus 2x), imamo (F21+√5(1 / 2))' = F'1+√5(1 / 2) · F'1+√5((1+√5) / 4) = 0 · (−2) = 0 < 1, iz čega možemo zaključiti da je taj 2-ciklus privlačan, što smo i prije mogli uočiti. 8. Bifurkacije, bifurkacijski dijagrami i Feigenbaumov atraktorNije teško primijetiti kako se razmatranje karakteristika logističke jednadžbe svodi na proučavanje nekih specifičnih točaka same funkcije i njezina parametra. Kako bi se lakše promatrale promjene koje se događaju zbog promjene parametra, razvijeni su prikazi fiksnih točaka logističke jednadžbe za određeni interval istog parametra. Sam prikaz sastoji se od grafa u λ-x0 koordinatnom sustavu koji se tada naziva i bifurkacijskim dijagramom, koji ćemo najbolje objasniti tako da pojasnimo značenje riječi bifurkacija. Generalno, bifurkacija (razdvajanje, viličenje) predstavlja događaj u kojem dolazi do nekog razdvajanja, a za nas bi bifurkacija predstavljala trenutak u kojem iz jedne privlačne fiksne točke logističke jednadžbe nastanu dvije vrijednosti. Ovaj se događaj pojavljuje samo u striktno određenim uvjetima koji, naravno, ovise o vrijednosti parametra i fiksne točke. Također valja reći da postoji nekoliko vrsta bifurkacija, no mi ćemo proučavati samo dvije vrste: bifurkaciju sedlo-čvor i udvostručenje perioda. U nastavku navodimo dovoljne uvjete za postojanje tih bifurkacija.
(8.1) Bifurkacija sedlo-čvor 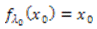
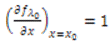

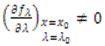
Tada postoji interval I oko x0 i glatka funkcija p : I → R takva da vrijedi Bifurkacijski dijagram tog slučaja izgleda ovako: 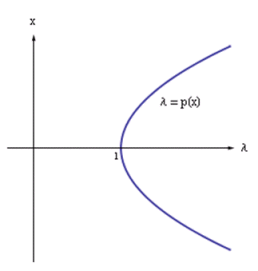
Pokušajmo sada naći vrijednost parametra logističkog preslikavanja kod kojeg dolazi do pojave bifurkacije sedlo-čvor. Tako imamo
Iz ovoga sustava dobivamo konkretne vrijednosti x0 = 0 i λ0 = 1 za koje se događa bifurkacija sedlo-čvor, što ćemo poslije jasno vidjeti na bifurkacijskom dijagramu. Ipak, valja napomenuti kako ove vrijednosti ne zadovoljavaju posljednji od spomenutih uvjeta, da vrijednost parcijalne derivacije funkcije f po parametru λ mora biti različita od 0, no ova bifurkacija je netipična te do bifurkacije ipak dolazi. 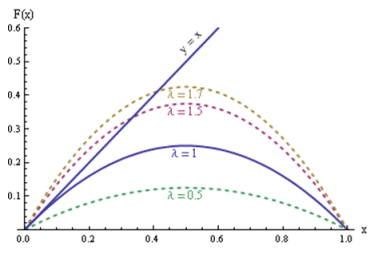
Zanimljiva vrijednost koja se odnosi na bifurkaciju sedlo-čvor jest "box dimenzija" niza (xn)n≥1 opisanog s xn+1 = Fλ0(xn) i prikladnom početnom vrijednosti x0 koja za logističko preslikavanje kod bifurkacije sedlo-čvor iznosi 1/2. Pojam fraktalne dimenzije vrlo se često javlja pri proučavanju ponašanja dinamičkih sustava, vidi [ZZ]. Više o fraktalnim dimenzijama može se pročitati na web stranicama [We] ili u knjizi [De]. Privlačni skupovi koji se javljaju kod diskretnih i kontinuiranih dinamičkih sustava, često imaju kompliciranu fraktalnu strukturu, pa nam fraktalna dimenzija daje dodatnu informaciju o takvim skupovima. Najčešće upotrebljavane fraktalne dimenzije su box dimenzija i Hausdorffova dimenzija. Box dimenzija jednaka je omjeru prirodnog logaritma broja sličnih objekata dobivenih podjelom originalnog objekta i prirodnog logaritma faktora skaliranja potrebnog kako bi se bilo koji od objekata dobivenih podjelom originalnog objekta sveo na veličinu originalnog objekta. Tako možemo lako izračunati dimenziju linije, kvadrata ili kocke jer znamo da ako liniju podijelimo na N segmenata jednake duljine, skaliranjem bilo kojeg od tih segmenata faktorom skaliranja N dobivamo segment jednake duljine kao i početna linija, te je tako njezina dimenzija jednaka 1. Slično, ako kvadrat podijelimo na N2 kvadrata jednake površine, tada skaliranjem faktorom N dobivamo kvadrat površine jednake početnoj, a dimenziju jednaku 2. Istim izračunom možemo dobiti vrijednost dimenzije kocke, a ona iznosi 3.
(7.2) Udvostručenje perioda 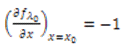
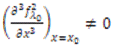
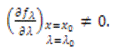
Tada postoji interval I oko x0 i glatka funkcija p : I → R takva da vrijedi Pokušajmo izračunati vrijednosti x0 i λ0 kod kojih dolazi do bifurkacije udvostručenja perioda kod logističkog preslikavanja. Tako imamo
iz čega dobivamo x0 = 2 / 3 i λ = 3, što se također jasno vidi na bifurkacijskom dijagramu. Kao i kod bifurkacije sedlo-čvor, moguće je izračunati box dimenziju niza opisanog na sličan način i ona iznosi 2/3. 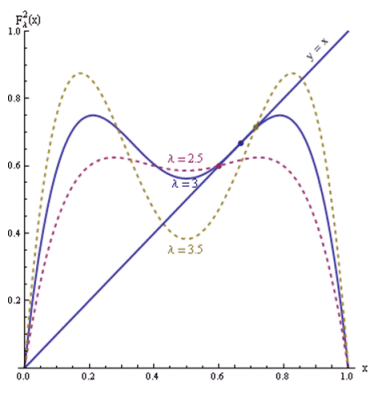
Bifurkacijski dijagram može se shvatiti kao grafički prikaz broja periodičkih točaka za određenu vrijednost parametra. Tako možemo vidjeti kako se za vrijednost parametra λ = 3 na grafu jasno vidi bifurkacija udvostručenja perioda te kako se broj periodičkih točaka eksponencijalno povećava kako vrijednost parametra raste. Ta pojava naziva se determinističkim kaosom. 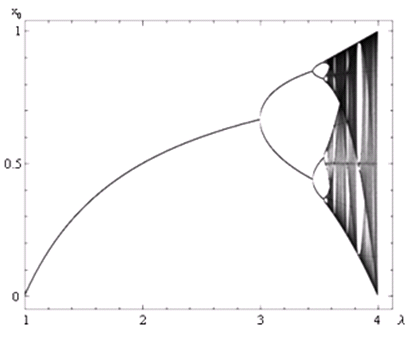
Pokušajmo sada približno izračunati vrijednosti parametara kod kojih dolazi do bifurkacije udvostručenja perioda. Svojedobno smo pokazali kako izračunavanje parametra za određenu n-orbitu zahtijeva promatranje rješenja sustava koji uključuje n-tu iteraciju Fλ(x). Budući da je taj sustav polinom n-tog stupnja, pronalaženje njegovih korijena je mukotrpan i, s povećanjem broja n, sve teži posao. Poznato je da za traženje nultočaka polinoma stupnja n > 4 ne postoji formula za egzaktno rješenje. U tu svrhu razvijen je jednostavan alat izračunavanja približne vrijednosti parametra za koji počinje iteriranje vrijednosti oko određene orbite. Formula koja se koristi u tu svrhu glasi
gdje je λ∞ ≈ 3.569945672, δ ≈ 4.66920160910299 - Feigenbaumova konstanta, λk - parametar kod kojeg počinje k-ta orbita i Γ ≈ 2.637. Možemo vidjeti na primjeru kako formula funkcionira. Znamo da je λ1 = 3, a uvrštavanjem u formulu dobiva se vrijednost 3.00518; za λ1 = 1 + √6 ≈ 3.44949 dobivena vrijednost približno iznosi 3.447339. Konstanta λ∞ koja se nalazi u formuli predstavlja vrijednost parametra kod kojeg je broj periodičkih točaka beskonačan, i predstavlja prag kaosa. Dio bifurkacijskog dijagrama nakon te vrijednosti naziva se Feigenbaumovim atraktorom te ima karakteristike fraktala, a strukturu poput Cantorova skupa. Slično kao i prije, moguće je izračunati fraktalne dimenzije Feigenbaumova atraktora te je moguće dobiti da je box dimenzija jednaka Hausdorffovoj dimenziji i približno iznosi 0.538. Tijekom ovog rada mogli smo vidjeti kako je proučavanje karakteristika i određivanje uvjeta u kojima te karakteristike dolaze na vidjelo odista složen postupak, koji zahtijeva dobru matematičku potporu. Čak i za neke jednostavnije sustave od logističkog preslikavanja, proučavanje ostaje posao koji se ne obavlja lako. Ipak, nakon provedenog istraživanja logističkog preslikavanja, možemo reći da njegove glavne karakteristike ovise o nekoliko jednadžbi iz kojih se računom dobivaju skupovi vrijednosti (fiksne točke, parametri) za koje logističko preslikavanje poprima specifična svojstva. Sljedeće tablice sadržavaju sumirane važne podatke o logističkom preslikavanju.
Kako bismo lakše vizualizirali složene situacije vezane za logističko preslikavanje, postoji niz računalnih programa koji služe za njihovo grafičko predočivanje. Jedan od njih je program dipl.inž. Radomira Stevanovića. Literatura
1. Uvod |