
Broj 2

















Zvonko Čerin
Geometrijski problem iz Latvije

Sadržaj:
ProblemDokaz teorema 1
Johnsonov teorem o tri kružnice i inverzija
Rješenje problema 1 pomoću računala
Još jedno rješenje problema 1 pomoću računala
Sugestije za istraživanja
Literatura
Download
 Geometry problem from Latvia (pdf)
Geometry problem from Latvia (pdf) 1. Problem
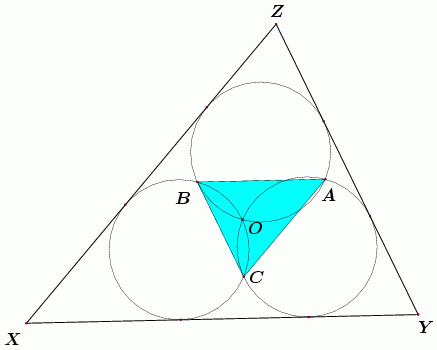
Na matematičkim natjecanjima 1994. godine u Latviji jedan od zadataka bio je i ovaj geometrijski problem (vidi [2], str. 8).Problem 1. Tri jednake kružnice sijeku se u točki O i također dvije po dvije u točkama A, B, C. Neka je T trokut dobiven iz presjeka zajedničkih tangenata tih kružnica. Neka kružnice leže unutar trokuta T. Pokažite da je površina trokuta T najmanje devet puta veća od površine trokuta ABC.
|
Slika 1. Površina
 XYZ
najmanje je devet puta veća od površine XYZ
najmanje je devet puta veća od površine
 ABC. ABC.
|
http://mathworld.wolfram.com/Nine-PointCircle.html
http://en.wikipedia.org/wiki/Nine_point_circle
http://planetmath.org/encyclopedia/NinePointCircle2.html
Teorem 1.
(a) Trokute ABC i UVW
povezuje homotetija h(F, -1),
gdje je F zajedničko središte njihovih
kružnica devet točaka.
(b) Postoji broj
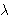
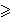 3
takav da je trokut XYZ pridružen trokutu
UVW homotetijom h(I,
3
takav da je trokut XYZ pridružen trokutu
UVW homotetijom h(I,
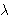 ),
gdje je I središte njemu upisane kružnice.
),
gdje je I središte njemu upisane kružnice.
|
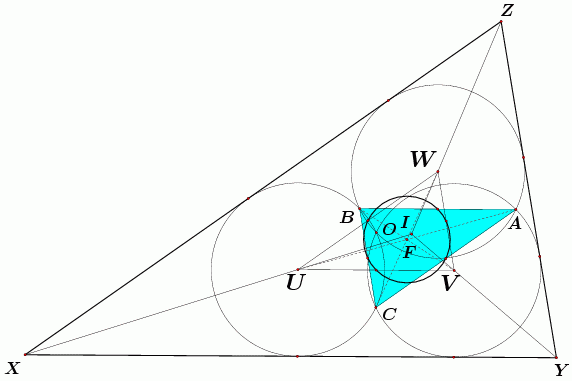
Slika 2. Za homotetije
h1 = h(F, -1) i
h2 = h(I,
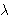 )
vrijedi ABC = h1(UVW) i
XYZ = )
vrijedi ABC = h1(UVW) i
XYZ = 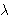
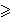 3. 3.
|
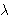
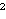
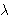
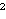
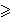 9
jer je
9
jer je 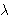
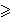 3.
3.
2. Dokaz teorema 1
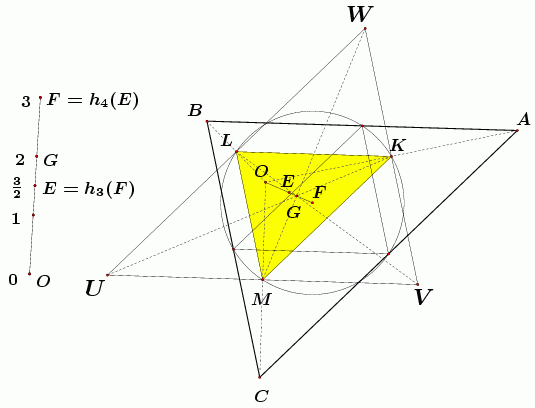
Dokaz teorema 1 (a): Kako su A, B, C refleksije središta O opisane kružnice trokuta UVW u njegovim stranicama, vidimo da su UVW i ABC pridruženi kompozicijom homotetija h3 = h(G, -1/2) i h4 = h(O,2), gdje je G težište trokuta UVW. Ta kompozicija je homotetija h1 = h(F, -1) jer je središte F kružnice devet točaka trokuta UVW njezina jedina fiksna točka (dakle, njezin centar), dok se konstante u kompoziciji homotetija množe. Točka F je središte kružnice devet točaka trokuta ABC jer homotetija h1 mora trokut KLM, komplementaran trokutu UVW (kojem su vrhovi polovišta stranica trokuta UVW), preslikati na trokut komplementaran trokutu ABC, kome vrhovi i dalje ostaju na kružnici devet točaka trokuta UVW budući da je homotetija h1 refleksija u točki F (vidi sliku 3).
|
Slika 3. Kompozicija UVW 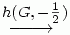 KLM KLM
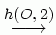 ABC
je homotetija h(F, -1). ABC
je homotetija h(F, -1).
|
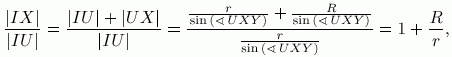
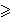 2,
slijedi da je konstanta
promatrane homotetije najmanje 3. Primijetimo
da se ta najmanja vrijednost postiže
jedino ako je trokut UVW
jednakostraničan.
2,
slijedi da je konstanta
promatrane homotetije najmanje 3. Primijetimo
da se ta najmanja vrijednost postiže
jedino ako je trokut UVW
jednakostraničan.

Iz prethodnog dokaza jasno je da vrijedi i
sljedeći teorem.
Teorem 2.
(a) Trokut XYZ ima najmanje tri puta
veći opseg od opsega trokuta ABC.
(b) Trokut XYZ ima tri puta veći
opseg od opsega trokuta ABC onda i samo
onda ako su trokuti ABC, UVW i
XYZ jednakostranični.
3. Johnsonov teorem o tri kružnice i inverzija
Konfiguracija triju kružnica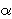 ,
,
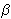 ,
,
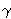 istog polumjera r koje se sijeku u točki
M spominje se ranije u
[5], [3] i
[4]. Tamo su Johnson i
Emch na više načina dokazali da ako se
te kružnice sijeku još i u točkama
P, Q, R, onda one leže na
kružnici
istog polumjera r koje se sijeku u točki
M spominje se ranije u
[5], [3] i
[4]. Tamo su Johnson i
Emch na više načina dokazali da ako se
te kružnice sijeku još i u točkama
P, Q, R, onda one leže na
kružnici 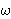 polumjera r (vidi sliku 4).
polumjera r (vidi sliku 4).
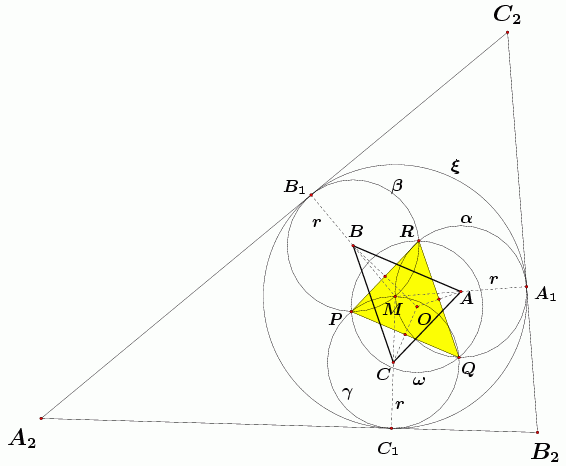
Mi smo tu tvrdnju usput dokazali u gornjem dokazu teorema 1. Sada ćemo prikazati njezin vrlo kratki dokaz korištenjem inverzije iz članka [4], gdje se opisuju i neki drugi problemi geometrije za koje je primjena inverzije također uspješna. Inverzija je transformacija ravnine koja je određena kružnicom. U knjizi [7] čitatelji mogu dobiti osnovne podatke o svojstvima tog preslikavanja i mnoštvo primjera njezine upotrebe u geometriji. Korisne informacije o inverziji mogu se naći i na web stranici http://mathworld.wolfram.com/Inversion.html.
|
| Slika 4. Johnsonov teorem o tri kružnice. |
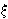 kojoj je središte točka M i koja dodiruje
stranice |B2C2|,
|C2A2|,
|A2B2|
u točkama A1,
B1, C1.
Slike pravaca B2C2,
C2A2,
A2B2
pri inverziji na kružnici
kojoj je središte točka M i koja dodiruje
stranice |B2C2|,
|C2A2|,
|A2B2|
u točkama A1,
B1, C1.
Slike pravaca B2C2,
C2A2,
A2B2
pri inverziji na kružnici
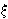 su kružnice
su kružnice
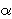 ,
,
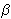 ,
,
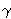 koje prolaze točkom M, diraju iznutra
kružnicu
koje prolaze točkom M, diraju iznutra
kružnicu 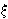 u točkama A1, B1,
C1 i imaju isti polumjer
r = |MA1|/2 =
|MB1|/2 = |MC1|/2.
Osim točke M, one se sijeku još u točkama
P, Q, R, koje određuju
kružnicu
u točkama A1, B1,
C1 i imaju isti polumjer
r = |MA1|/2 =
|MB1|/2 = |MC1|/2.
Osim točke M, one se sijeku još u točkama
P, Q, R, koje određuju
kružnicu 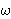 (opisanu kružnicu trokuta PQR).
(opisanu kružnicu trokuta PQR).
Promatrajmo sada refleksije
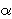 ',
',
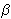 ',
',
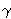 '
kružnica
'
kružnica 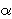 ,
,
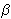 ,
,
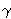 u pravcima QR, RP, PQ.
One imaju isti polumjer r, a središta im
leže na simetralama stranica |QR|,
|RP|, |PQ| koje se sijeku u
središtu O kružnice
u pravcima QR, RP, PQ.
One imaju isti polumjer r, a središta im
leže na simetralama stranica |QR|,
|RP|, |PQ| koje se sijeku u
središtu O kružnice
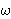 .
Zato se kružnice
.
Zato se kružnice
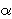 ',
',
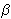 ',
',
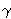 '
podudaraju s kružnicom
'
podudaraju s kružnicom
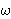 .
.
Nadopunimo li sliku 4 sada trokutom XYZ
iz zajedničkih tangenata kružnica
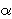 ,
,
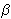 ,
,
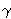 ,
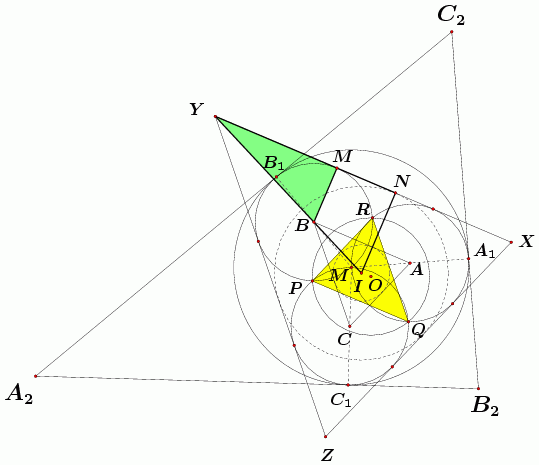
na slici 5 se iz sličnih trokuta BMY i
INY lijepo vidi da su ABC i
XYZ povezani homotetijom kojoj je
središte zajedničko središte I
upisanih kružnica trokuta ABC i XYZ
i da je omjer te homotetije 1 +
r/
,
na slici 5 se iz sličnih trokuta BMY i
INY lijepo vidi da su ABC i
XYZ povezani homotetijom kojoj je
središte zajedničko središte I
upisanih kružnica trokuta ABC i XYZ
i da je omjer te homotetije 1 +
r/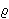 ,
gdje su r i
,
gdje su r i
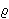 polumjeri trokutu ABC
opisane i upisane kružnice, a M i N
su projekcije od B i I na
pravac XY.
polumjeri trokutu ABC
opisane i upisane kružnice, a M i N
su projekcije od B i I na
pravac XY.
|
Slika 5. Trokute ABC i XYZ
povezuje homotetija h(I, 1 +
r/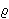 ). ).
|
4. Rješenje Problema 1 pomoću računala
Drugo rješenje problema 1: Sada ćemo opisati kako se problem 1 može riješiti uz pomoć računala. Pri tome koristimo analitičku geometriju ravnine i složeni program Maple V. Napominjemo da su sve nedefinirane funkcije koje koristimo objašnjene u članku [1].
Bez smanjenja općenitosti možemo
pretpostaviti da su kutovi U i V
promatranog trokuta UVW oštri (tj.
manji od
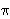 /2
/2
assume(f>1, g>1): tU:=[0,0]: tV:=[f+g,0]: tI:=[f,1]:
Ideja dokaza je naći koordinate vrha W i središta O opisane kružnice, što će nam omogućiti da izračunamo radijus R opisane kružnice i da onda odredimo koordinate vrhova trokuta XYZ i ABC i da pokažemo da je omjer njihovih površina najmanje 9. Ako su Ja, Jb, Jc projekcije središta I upisane kružnice na stranice, onda Jc ima koordinate (f, 0), a koordinate Ja dobivamo iz sustava jednadžbi
tJc:=[f,0]: tT:=[p,q]: u:=(x,y)->udaljenost(x,y):
rJa:=solve({u(tV,tT)=u(tV,tJc), u(tI,tT)=1}, {p,q});
tJa:=subs(rJa[2],tT):
rJb:=solve({u(tU,tT)=u(tU,tJc), u(tI,tT)=1}, {p,q});
tJb:=subs(rJb[2],tT);
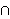 VJa.
VJa.
tW:=presjek(pravac2(tV,tJa), pravac2(tU,tJb));
h:=x->u(x,tT)=R: rOR:=solve({h(tU),h(tV),h(tW)}, {p,q,R});
tO:=subs(rOR,tT): vR:=subs(rOR,R):
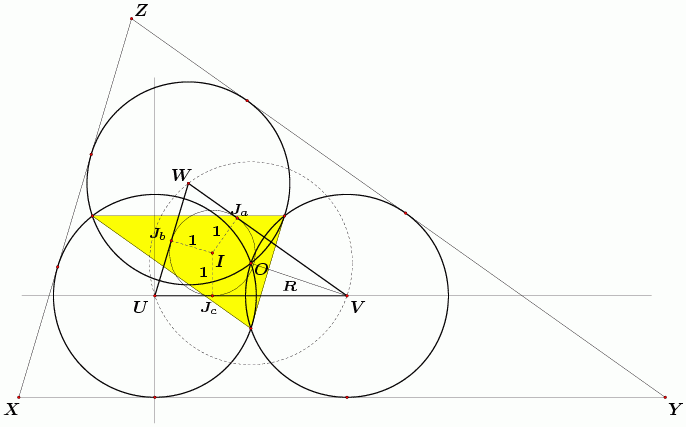
|
| Slika 6. Određivanje koordinata točaka W i O, te radijusa R. |
k:=x->u(x,tT)^2-vR^2: s:=(x,y)->solve({k(x),k(y)}, {p,q}):
rA:=s(tV,tW): rB:=s(tW,tU): rC:=s(tU,tV):
tA:=subs(rA[2],tT); tB:=subs(rB[2],tT); tC:=subs(rC[2],tT);
tX:=[x,a]: tY:=[y,b]: tZ:=[z,c]:
j:=(x,y,z,w)->paralelniQ(pravac2(x,y), pravac2(z,w)):
k:=(x,y,z)->u(x, projekcija(x, pravac2(y,z)))^2-vR^2:
rj:=solve({j(tY,tZ,tV,tW),j(tZ,tX,tW,tU),j(tX,tY,tU,tV),
k(tX,tU,tV),k(tY,tV,tW),k(tZ,tW,tU)}, {x,a,y,b,z,c}):
tX:=subs(rj[3],tX): tY:=subs(rj[3],tY): tZ:=subs(rj[3],tZ):
raz:=FS(povrsina(tX,tY,tZ)/povrsina(tA,tB,tC)-9);
Maple V će izračunati da je gornja razlika jednaka
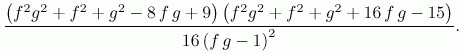
Druga zagrada u brojniku uvijek je pozitivna
jer je fg > 1, pa je 16fg > 16 i
zato f2g2 +
f2 + g2 +
16fg - 15 > 4.
Promatrajmo prvu zagradu u brojniku kao
polinom u varijabli f. Uz pomoć Maple
V nadopunimo ga do punog kvadrata.
with(student): pz:=completesquare(op(2,raz),f):
FS(op(1,pz)); FS(pz-op(1,pz));
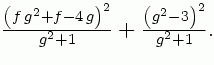
To je očigledno uvijek pozitivno osim za f = √3 i g = √3, kada je nula.

5. Još jedno rješenje problema 1 pomoću računala
Da netko ne bi pomislio da se pomoću računala problemi mogu rješavati samo na jedan način, sada ćemo opisati još jedno rješenje, koje je nešto kraće.Polazimo od toga da trokut XYZ ima standardnu parametrizaciju s kotangensima f > 1 i g > 1 polovica kutova X i Y i polumjerom upisane kružnice jednakim 1.
assume(f>1, g>1): tX:=[0,0]: tY:=[f+g,0]: tI:=[f,1]:
tZ:=[g*(f^2-1)/(f*g-1), 2*f*g/(f*g-1)]:
o:=x->omjermn(x,tI,r,1-r): tU:=o(tX): tV:=o(tY): tW:=o(tZ):
Točka O je za r udaljena od točaka U, V i W. Ta tri uvjeta omogućavaju da nađemo koordinate točke O i pozitivni broj r, koji mora biti manji od 1 jer tri kružnice leže u trokutu XYZ.
tO:=[p,q]: u:=(x,y)->udaljenost(x,y)^2 - r^2:
rO:=solve({u(tU,tO), u(tV,tO), u(tW,tO), r<1}, {p,q,r});
s:=x->subs(rO,x): tU:=s(tU): tV:=s(tV): tW:=s(tW): tO:=s(tO):
r:=(x,y,z)->refleksijaP(x,pravac2(y,z)):
tA:=r(tO,tV,tW): tB:=r(tO,tU,tW): tC:=r(tO,tV,tU):
raz:=FS(povrsina(tX,tY,tZ)/povrsina(tA,tB,tC)-9);
Maple V će ponovo izračunati da je gornja razlika jednaka
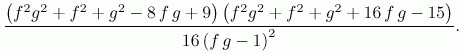
6. Sugestije za istraživanja
Jedna od čarobnih privlačnosti matematike njezino je bogatstvo mogućnosti, tako da nam čak i naivna pitanja o nekom problemu, poput ovog našeg iz Latvije, otvaraju mnoštvo novih problema. Taj proces neki nazivaju matematičkim mjesečarenjem. Tako ću i ja sada malo mjesečariti o problemu iz Latvije.Prva jednostavna ideja je da se poveća broj kružnica.
Problem 2.
Četiri jednake kružnice
k1, k2,
k3, k4
sijeku se u točki O i također
k1 i k2,
k2 i k3,
k3 i k4,
k4 i k1
u točkama A, B, C, D.
Neka je T četverokut dobiven iz presjeka
zajedničkih tangenata tih kružnica.
Neka kružnice leže unutar
četverokuta T. Pokažite da je
površina četverokuta T najmanje
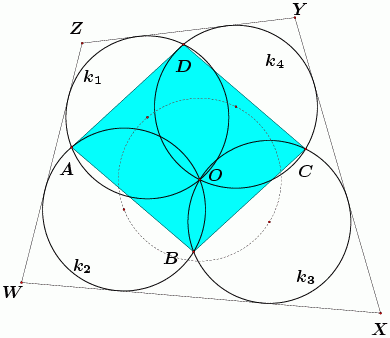
(3+2√2)/2 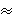 2.9142 puta veća od površine četverokuta ABCD.
2.9142 puta veća od površine četverokuta ABCD.
|
| Slika 7. Slučaj četverokuta. |
Druga je mogućnost izbaciti zahtjev da promatrane kružnice imaju isti radijus. Taj slučaj možemo iskazati ovako.
Problem 3. Neka je P točka u ravnini trokuta ABC koja nije na njemu opisanoj kružnici ni na pravcima BC, CA, AB i neka je XYZ trokut dobiven iz zajedničkih tangenti kružnica ka, kb, kc opisanih trokutima BCP, CAP, ABP, tako da on sadrži kružnice. Ocijenite koliki je omjer površina trokuta XYZ i ABC.
Ako trokut ABC nije pravokutan, onda kružnice ka, kb, kc nisu identične i imaju iste radijuse onda i samo onda ako je točka P ortocentar H trokuta ABC. Kad je ABC pravokutan trokut, takva točka ne postoji. Dakle, u teoremu 1 točka O je ortocentar (presjek visina) trokuta ABC.
Poteškoće u pokušajima rješavanja ovih problema i njihovoj približnoj provjeri u programu Sketchpad dolaze zato što dvije kružnice općenito imaju i do četiri zajedničke tangente, pa je nemoguće napisati jednadžbu ili konstruirati točno onu tangentu koja nama treba. Izrazi za jednadžbe tangenti zbog složenosti i pojave kvadratnih korijena praktički su neupotrebljive. Zato se moramo dosjetiti nekom triku ili novom pametnom pristupu rješavanju ovih problema.
Ipak možemo pokušati nešto
reći o omjeru zbroja
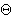 površina kružnica
ka,
kb,
kc
i površine S trokuta ABC.
površina kružnica
ka,
kb,
kc
i površine S trokuta ABC.
Problem 4.
Za bilo koju točku izvan pravaca BC,
CA, AB omjer
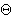 /S
iznosi najmanje (4π√3)/3
/S
iznosi najmanje (4π√3)/3
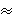 7.2552.
7.2552.
Jedino što autor članka zasad može dokazati jest da je za
pojedine značajne (tzv. centralne)
točke P trokuta ABC
(vidi [6])
omjer 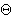 /S
veći od nekih konkretnih brojeva koji su
nešto manji od broja (4π√3)/3.
Tipičan takav rezultat jest ovaj teorem.
/S
veći od nekih konkretnih brojeva koji su
nešto manji od broja (4π√3)/3.
Tipičan takav rezultat jest ovaj teorem.
Teorem 3.
Ako je P središte I upisane
kružnice trokuta ABC, onda je omjer
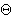 /S
veći od
(14π)/9
/S
veći od
(14π)/9
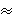 4.8869.
4.8869.
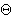 /S -
(14π)/9 jednaka je
/S -
(14π)/9 jednaka je 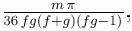 gdje nam m označava polinom
gdje nam m označava polinom
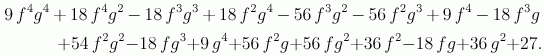
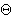 /S
≥ (14π)/9 i dokaz je završen.
/S
≥ (14π)/9 i dokaz je završen.

Literatura
[1] M. Bator, Z. Čerin i M. Ćulav, Analitička geometrija ravnine računalom,Matematičko-fizički list, 54 (2003/2004), 36-47.
[2]
Crux Mathematicorum with Mathematical Mayhem,
Volume 23, February 1997.
[3] A. Emch, Remarks on the foregoing circle theorem, American Mathematical Monthly, 23 (1916), 162-164.
[4] A. Emch, Rare problems in plane geometry, Scripta Math., 16 (1950), 61-66.
[5] R. A. Johnson, A circle theorem, American Mathematical Monthly, 23 (1916), 161-162.
[6] C. Kimberling, Encyclopedia of
Triangle Centers, 2000.
http://faculty.evansville.edu/ck6/encyclopedia/
[7] D. Palman, Trokut i kružnica, Element, Zagreb, 1994.
Download
 Engleska verzija teksta u PDF formatu
Engleska verzija teksta u PDF formatu Maple V (verzija 9) bilježnica (notebook) - omogućuje provjeru svih izračuna u članku
Problem
Dokaz teorema 1
Johnsonov teorem o tri kružnice i inverzija
Rješenje problema 1 pomoću računala
Još jedno rješenje problema 1 pomoću računala
Sugestije za istraživanja
Literatura
Download