
 |
Hrvatski matematički elektronski časopis math.e | |
| Broj 10 | ||
| http://e.math.hr/ |
Sadržaj:
1. Uvod
2. René Descartes
3. Osnovne formule analitičke geometrije
4. Zadaci za osnovnu školu
5. Zadaci za srednju školu
Literatura
Download
Prije dvije godine na PMF-Matematičkom odjelu u Zagrebu studij za nastavnike matematike počeo se izvoditi po novom planu i programu. Jedan od glavnih ciljeva novog programa studija je da se studenti - budući nastavnici matematike - upoznaju sa što više oblika nastave matematike koji se izvode u osnovnim i srednjim školama. U novom programu studija velik naglasak stavljen je na seminare, tj. želi se da budući nastavnici budu što više u situacijama izlaganja matematičkog sadržaja. Tako se na trećoj godini studija nastavničkih smjerova izvodi kolegij Seminar - Natjecanja iz matematike. Bit tog seminara je da studenti u grupama obrade zadatke s raznih nivoa natjecanja iz matematike u okviru odabrane teme (naglasak je stavljen na natjecanja u Republici Hrvatskoj).
Ovaj članak nastao je na osnovi našeg seminara s temom "Koordinatni sustav". Zadatak nam je bio pokušati seminar koncipirati tako da može poslužiti kao materijal nastavnicima za dodatnu nastavu matematike. Nadamo se da smo u tome donekle uspjele.
U prvom dijelu članka navele smo kratak povijesni uvod i ponovile osnovne formule analitičke geometrije koje se koriste pri rješavanju zadataka. Nakon toga slijede zadaci s natjecanja koje smo odabrale s uputama za rješavanje i našim komentarima. Napominjemo da je većina zadataka koje smo uvrstile namijenjena učenicima sedmog i osmog razreda osnovne škole te trećeg i četvrtog razreda srednje škole, jer se upravo tada po nastavnom planu obrađuju teme iz analitičke geometrije.
Prilikom rješavanja zadataka i izrade slika koristile smo se računalnim programima The Geometer's Sketchpad i GeoGebra. Namjera nam je bila rješenja zadataka učiniti jednostavnijima, dinamičnijima, odnosno zornijima. Na tim se materijalima GeoGebra pokazala kao moćan alat za demonstriranje konstrukcija korak po korak. Neke od dinamičkih slika uvrštene su u ovaj članak kao Java appleti.
Zahvaljujemo voditelju seminara o natjecanjima iz matematike, doc.dr.sc. Mladenu Vukoviću, na pomoći pri pisanju članka.
Jedno od važnijih matematičkih otkrića prve polovine 17. stoljeća je ideja o koordinatama i koordinatnom sustavu. Prvi ju je jasno izložio i razradio francuski matematičar René Descartes, rođen 31. ožujka 1596.
Godine u kojima je živio bile su bez sumnje jedan od velikih intelektualnih perioda u povijesti civilizacije. Spomenut ćemo nekoliko njegovih znamenitih suvremenika: od matematičara tu su Fermat i Pascal; Shakespeare je umro kad je Descartesu bilo dvadeset godina; Descartes je za osam godina nadživio Galileija, a umro je kad je Newtonu bilo osam godina.
Kada mu je bilo osam godina, otac ga upisuje u isusovačku školu. Tamošnji rektor otac Charlet zavolio je blijedog, prostodušnog dječaka i posebno ga učio. Uvijek je htio znati uzrok svega pod suncem. Njegovo krhko zdravlje zahtijevalo je da se više odmara. Stoga je često ujutro ostajao dugo u krevetu i razmišljao; ta tiha jutra bila su pravi izvor njegove filozofije i matematike. Smatrao je da su sve znanosti međusobno povezane. Tako je stečena znanja, od matematike do filozofije i medicine, dalje razvijao, ulazio u probleme te ih nastojao riješiti.
Besmrtnu slavu Descartes je stekao otkrićem analitičke geometrije. Zanimljiva je mala povijest tog otkrića. U vojničkom periodu njegova života, u noći 10. studenog 1619., usnuo je tri čudesna sna. Tvrdio je da mu se tada otkrio čarobni ključ koji otvara riznicu prirode i daje mu temelj svih znanosti. Nigdje nije točno objasno što je taj ključ, ali se vjeruje da je to primjena algebre u geometriji - analitička geometrija i, znatno općenitije, objašnjenje prirodnih pojava pomoću matematike. Zbog ratnih i drugih okolnosti otkriće će ostati nepoznato osamnaest godina. Veličinu Descartesova otkrića ne umanjuje ni činjenica da on nije imao koordinatni sustav u današnjem smislu riječi. Descartesov koordinatni sustav ima ishodište, ima samo jednu os (apscisu), dok drugu os uspostavlja prema nužnosti. Njegov je koordinatni sustav kosokutni, a vladanje krivulja proučava samo u prvom kvadrantu. Danas se koordinatni sustav po latiniziranom prezimenu Cartesius naziva Kartezijevim koordinatnim sustavom.
U pedesetoj godini života Descartes je živio u Nizozemskoj razmišljajući, obrađujući mali vrt i dopisujući se s intelektualcima Europe. Njegov najveći matematički rad bio je iza njega, ali je još uvijek razmišljao o matematici, uvijek prodorno i originalno. Bio je poznat u svijetu, mnogo poznatiji nego što je uopće ikada želio biti. Za njega je čula devetnaestogodišnja švedska kraljica Kristina te ga zamolila da ju dođe podučavati. Ambiciozna kraljica zahtijevala je satove učenja u ranu zoru, a Descartes bi se poslušno izvlačio iz kreveta, popeo u kočiju i vozio se kroz puste vjetrovite ulice Stockholma u kraljevsku palaču, gdje je Kristina sjedila u ledenoj biblioteci i nestrpljivo čekala da njezin sat filozofije počne točno u pet sati ujutro. Descartes nije mogao podnijeti hladnoću švedske zime te se razbolio od upale pluća. Zabrinuta kraljica pozvala je liječnike, no on ih je odbijao. Umro je 11. veljače 1650. u pedesetčetvrtoj godini života, kao žrtva hirova kraljice Kristine.
Ponovimo ukratko najvažnije pojmove i činjenice o koordinatnom sustavu na pravcu i u ravnini.
Neka je T točka na brojevnom pravcu. Njoj je pridružen neki broj x, što zapisujemo T(x). Broj x nazivamo koordinatom točke T. Neka je x1 koordinata točke A i x2 koordinata točke B. Tada se udaljenost između tih točaka računa formulom |AB| = |x1 − x2|. Koordinata polovišta P dužine AB dana je formulom
| xP = | x1 + x2 | . |
| 2 |
Neka su u pravokutnom koordinatnom sustavu u ravnini dane točke A(x1, y1) i B(x2, y2). Tada njihovu udaljenost računamo formulom
| |AB| = | \ | (x1−x2)2 + (y1−y2)2 | . |
Točkama A i B zadana je dužina AB. Koordinate njenog polovišta P(xP, yP) računaju se formulama
| xP = | x1 + x2 | , | yP = | y1 + y2 | . |
| 2 | 2 |
Kroz dvije različite točke ravnine prolazi točno jedan pravac. Ako su apscise točkaka A i B različite, jednadžba tog pravca dana je formulom
| y − y1 = | y2 − y1 | (x − x1) . |
| x2 − x1 |
Broj
| k = | y2 − y1 |
| x2 − x1 |
nazivamo koeficijentom smjera pravca AB. Jednadžbu tog pravca možemo kraće zapisati kao y = kx + l, pri čemu je l = y1 − kx1.
Ponovimo još i jednadžbe krivulja drugog reda. Jednadžba kružnice k(S, r) radijusa r sa središtem u točki S(x0, y0) dana je formulom
Pravac koji s krivuljom drugog reda ima samo jednu zajedničku točku naziva se njezinom tangentom. Jednadžba tangente na kružnicu k(S, r) u njenoj točki T1(x1, y1) ima jednadžbu
Jednadžba elipse s velikom poluosi a, malom poluosi b i središtem u ishodištu glasi
| x2 | + | y2 | = 1. |
| a2 | b2 |
Tangenta na elipsu u njenoj točki T1(x1, y1) ima jednadžbu
| x1 x | + | y1 y | = 1. |
| a2 | b2 |
Jednadžba hiperbole s velikom poluosi a, malom poluosi b i središtem u ishodištu glasi
| x2 | − | y2 | = 1. |
| a2 | b2 |
Tangenta na hiperbolu u njenoj točki T1(x1, y1) ima jednadžbu
| x1 x | − | y1 y | = 1. |
| a2 | b2 |
Jednadžba parabole kojoj se os podudara s x-osi, a tjeme joj je u ishodištu je oblika
za neki p ≠ 0. Tangenta na parabolu je pravac koji nije paralelan s x-osi i siječe je u jednoj točki T1(x1, y1). Jednadžba tog pravca glasi
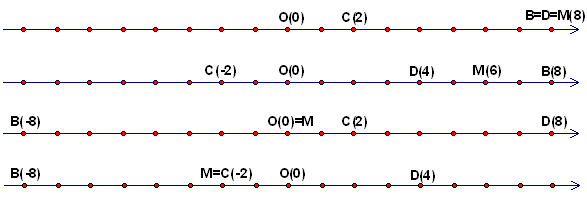
U koordinatnom sustavu na pravcu kojem je točka O ishodište, odabrane su točke B, C, D tako da je |OB| = 8, |OC| = 2, |CD| = 6 te točka M koja je polovište dužine BD. Odredite koordinate točaka D i M ako je koordinata točke D pozitivna. Ispitajte sve slučajeve!
U ovom zadatku zahtijeva se učenikovo snalaženje i orijentacija u koordinatnom sustavu na pravcu.
Rješenje. Budući da je |OB| = 8, točka B može imati koordinate 8 i -8, a točka C koordinate 2 i -2 pa imamo sljedeća četiri slučaja:
Pravac p … 3x − 4y − 1 = 0 siječe pravac a … y = (5/3)x − 3 u točki A, a pravac b … 5x + 4y − 55 = 0 u točki B. Izračunaj udaljenost između točaka A i B.
Zadatak je lako rješiv ako se zna formula za udaljenost dviju točaka u ravnini, ali se ona ne obrađuje u 8. razredu. Stoga je bitno doći do ideje kako primjenom Pitagorina poučka izračunati udaljenost između točaka A i B.
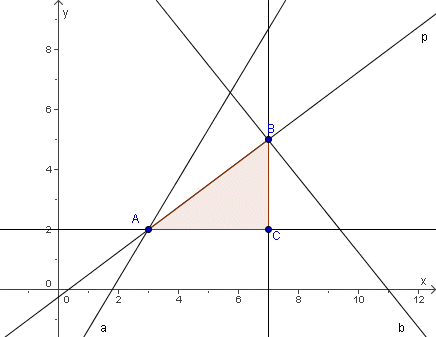
Rješenje. Tražimo sjecište pravaca p i a da bismo dobili koordinate točke A i sjecište pravaca p i b da bismo dobili koordinate točke B. Rješavamo dva sustava jednadžbi:
| p … | 3x − 4y − 1 = 0 | p … | 3x − 4y − 1 = 0 | |
| a … | y = (5/3)x − 3 | b … | 5x + 4y − 55 = 0 |
Rješenja su koordinate točaka A(3, 2) i B(7, 5). Udaljenost između tih točaka naći ćemo pomoću Pitagorina poučka primijenjenog na pravokutan trokut ABC. Točku C(7, 2) zadajemo kao sjecište pravaca x = 7 (apscisa od B) i y = 2 (ordinata od A). Udaljenosti |AC| = 4 i |BC| = 3 znamo naći iz jednadžbe za udaljenost dviju točaka na pravcu. Primjenom Pitagorina poučka izračunamo udaljenost između točaka A i B: √42 + 32 = 5.
Točka A(−4, 2) je vrh trokuta ABC. Na pravcu p1 … y = 3x − 7 leži stranica BC, a na pravcu p2 … y = 2x + 8 leži visina iz vrha C na stranicu AB. Kolike su koordinate vrhova B i C trokuta ABC?
Ovdje je bitno odrediti koji pravci su okomiti, kako doći do njihovih jednadžbi te postupak računanja koordinata točaka.
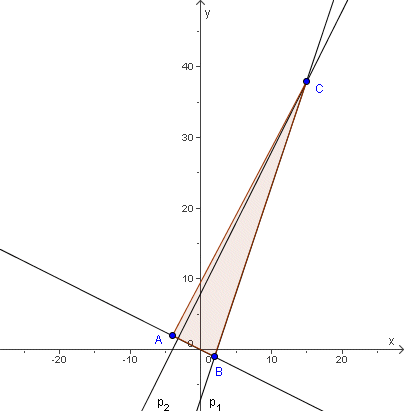
Rješenje. Točka C je sjecište pravaca p1 i p2. Rješavamo sustav jednadžbi
| p1 … | y = 3x − 7 |
| p2 … | y = 2x + 8 |
i dobivamo koordinate vrha C(15, 38). Pravac AB prolazi kroz A i okomit je na pravac p2 pa je njegov koeficijent smjera recipročan i suprotnog predznaka, tj. jednak je -1/2. Jednadžba pravca AB lako se dobije uvrštavanjem koordinata točke A u formulu za jednadžbu pravca zadanog točkom i koeficijentom smjera: y = −(1/2)x. Koordinate vrha B(2, −1) dobijemo rješavanjem sustava linearnih jednadžbi, kao sjecište pravaca AB i p1.
Jednadžba pravca p je 4x − 3y − 8 = 0, a jednadžba pravca q je y = −x + 8. Točka A je presjek pravaca p i x-osi, točka B je presjek pravaca q i x-osi, a točka C presjek pravaca p i q. Kolika je površina trokuta ABC?
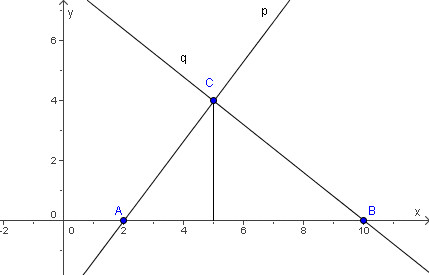
Rješenje. Za računanje površine potrebno je naći udaljenost između točaka A i B te duljinu visine iz vrha C na stranicu AB. Koordinate vrhova trokuta nalazimo kao presjeke dvaju pravaca, rješavanjem sustava jednadžbi: A(2, 0), B(10, 0) i C(5, 4). Bitno je uočiti da je duljina visine na stranicu AB jednaka ordinati vrha C. Iz toga i iz udaljenosti |AB| = 8 možemo izračunati površinu P(ABC) = 8·4 / 2 = 16.
Stranice trokuta ABC leže na pravcima čije jednadžbe su y = −2x + 10, y = (3/2)x − 1/2 i x + 4y − 5 = 0. Izračunaj koordinate vrhova trokuta ABC i njegovu površinu te ga nacrtaj u koordinatnom sustavu.
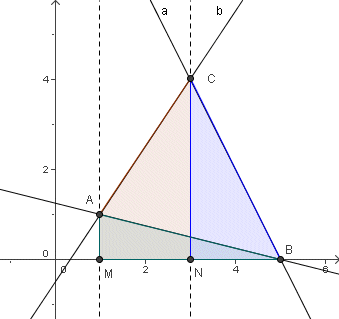
Rješenje. Koordinate vrhova A(1, 1), B(5, 0) i C(3, 4) nalazimo kao u prethodnim zadacima, rješavanjem sustava jednadžbi. Kad nacrtamo trokut ABC u koordinatnoj ravnini, uočavamo da se njegova površina može izračunati pomoću trapeza MNCA i trokuta NBC i AMB. Te površine možemo izračunati kao u zadatku 4.4. Rješenje je P(ABC) = P(MNCA) + P(NBC) − P(AMB) = 5 + 4 − 2 = 7.
Točke A(3, 0) i C(-4, 1) dva su nasuprotna vrha kvadrata ABCD. Odredite koordinate vrhova B i D ako vrh B leži na pozitivnom dijelu osi y.
U ovom zadatku bitno je poznavanje svojstva kvadrata da se dijagonale sijeku pod pravim kutom i međusobno raspolavljaju, formule za polovište dužine i odnos koeficijenata smjera okomitih pravaca.
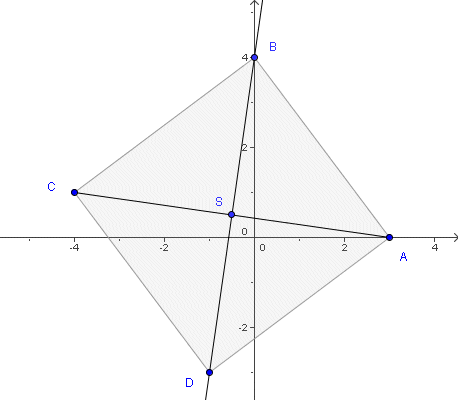
Rješenje. Dužina AB je dijagonala kvadrata. Njezino je polovište središte kvadrata S(−1/2, 1/2), a pravac na kojem leži dobivamo uvrštavanjem koordinata točaka A i C u jednadžbu pravca određenog dvjema točkama: y = −(1/7)x+3/7. Pravac BD okomit je na pravac AC i prolazi točkom S te ga lako dobijemo po formuli: y = 7x + 4. Sjecište y-osi i pravca BD je točka B(0, 4). Točku D(-1, -3) dobijemo iz formula za koordinate polovišta dužine u ravnini.
Alternativno, točku B možemo odrediti korištenjem Pitagorina poučka: |AB| = |BC| ⇒ |AC|2 = 2|AB|2. Uzimajući u obzir da se točka B nalazi na pozitivnom dijelu y-osi nalazimo njezine koordinate B(0, 4). Koordinate točke D dobivamo na prethodno opisani način.
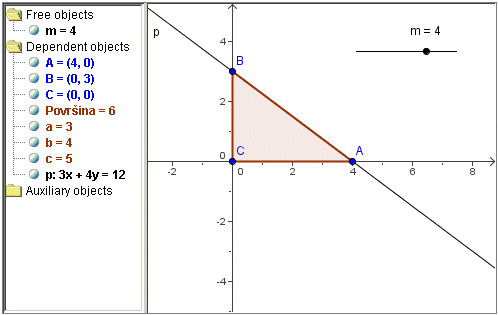
Odredite sve vrijednosti parametra m tako da pravac p … 3x + my = 12 određuje s koordinatnim osima trokut površine 6.
|
Rješenje. Ovaj zadatak najlakše možemo riješiti primjenom segmentnog oblika jednadžbe pravca
| x | + | y | = 1. |
| a | b |
Brojevi a i b imaju geometrijsko značenje, naime (a, 0) i (0, b) su koordinate presjeka pravca s koordinatnim osima. Zapišimo jednadžbu pravca p u segmentnom obliku:
| x | + | y | = 1. |
| 4 | 12/m |
Sada direktno možemo iščitati koordinate presjeka pravca s koordinatnim osima, tj. koordinate točaka A(4, 0) i B(0, 12/m). Budući da je trokut pravokutan, njegova je površina
| P(OAB) = | |OA|·|OB| | = | 4·|OB| | = 6 ⇒ |OB| = 3. |
| 2 | 2 |
Iz toga lako dođemo do traženog parametra m. Obratimo pažnju na to da točka B može biti na pozitivnom ili negativnom dijelu y-osi, što nam daje dva rješenja m = 4 i m = −4.
Nađite duljinu zajedničke tetive kružnica x2 + y2 − 2x − 4y − 4 = 0 i x2 + y2 − 3x + 4y = 0. Koliko ima zajedničkih tangenata? Nađite njihove jednadžbe i udaljenosti između njihovih dirališta s kružnicama.
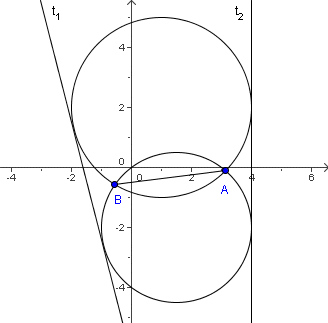
Rješenje. Oduzimanjem jednadžbi kružnica dobivamo x = 8y + 4. To je jednadžba pravca na kojem leži zajednička tetiva; želimo odrediti presjek tog pravca s kružnicama. Uvrštavanjem x = 8y + 4 u jednadžbu druge kružnice, nakon sređivanja dobivamo kvadratnu jednadžbu 65y2 + 44y + 4 = 0. Rješenja te jednadžbe su y1,2 = (−22 ± 4√14)/65, a odgovarajuće x-koordinate x1,2 = (84 ± 32√14)/65. Tako smo dobili koordinate krajnjih točkaka A i B zajedničke tetive kružnica. Duljinu tetive izračunamo po formuli za udaljenost dviju točaka ravnine: |AB| = 8√14/65.
Da bismo nacrtali kružnice, napišimo im jednadžbe u obliku (x − 1)2 + (y − 2) = 32 i (x − 3/2)2 + (y + 2) = (5/2)2, iz kojih vidimo koordinate središta i polumjere. Na slici uočavamo da je jedna zajednička tangenta vertikalni pravac x = 4 koji dodiruje kružnice u točkama (4, 2) i (4, −2). Druga dva dirališta možemo dobiti zrcaljenjem s obzirom na simetralu dužine AB. Simetrala prolazi kroz središta kružnica (1, 2) i (3/2, −2), pa joj lako izračunamo jednadžbu s … y = −8x + 10. Uz malo više računanja dolazimo do koordinata točaka simetričnih točkama (4, 2) i (4, −2) s obzirom na pravac s: (−124/65, 82/65) i (−12/13, −34/13). To su dirališta druge zajedničke tangente, koja ima jednadžbu 63x + 16y + 100 = 0. Udaljenost dirališta na istoj tangenti je 4.
U elipsu b2x2 + a2y2 = a2b2 (sa središtem u ishodištu) upisan je trokut ABC tako da je tangenta na elipsu u svakom njegovom vrhu paralelna s nasuprotnom stranicom trokuta. Kolika je površina tog trokuta ako je C(0, b)?
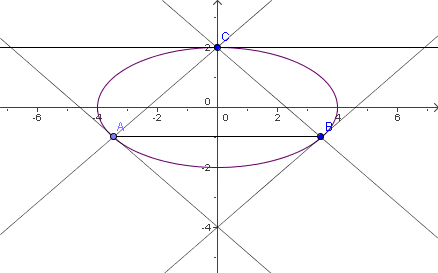
Rješenje. Tangenta na elipsu u točki C je paralelna s x-osi, pa je i pravac AB paralelan s x-osi. Neka je njegova jednadžba y = m. Koordinate točaka A i B dobijemo kao sjecišta elipse i tog pravca:
| A ( | −a √b2 − m2 | , m) , B ( | a √b2 − m2 | , m) . |
| b | b |
Tangenta na elipsu kroz točku A paralelna je s pravcem BC, pa su im koeficijenti smjera jednaki. Koeficijent smjera tangente dobije se uvrštavanjem koordinata točke A u jednadžbu tangente na elipsu:
| kA = | b √b2 − m2 | . |
| am |
Koeficijent smjera pravca BC izračuna se iz jednadžbe pravca kroz dvije točke:
| kBC = | b (m − b) | . |
| a √b2 − m2 |
Izjednačavanjem tih dvaju koeficijenata smjera dobivamo m = −b/2. Točke A i B imaju koordinate (±√3a/2, −b/2), iz čega lako izračunamo površinu P(ABC) = 3√3ab/4.
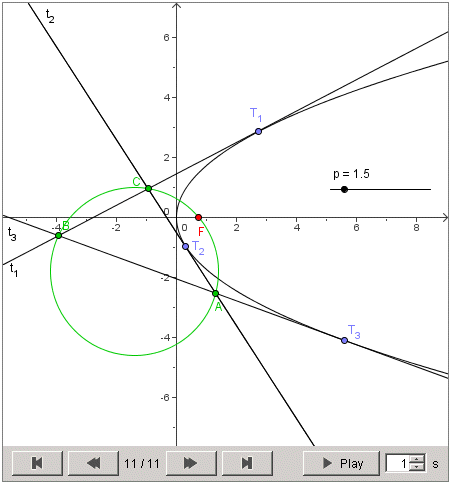
Tri tangente parabole određuju trokut. Dokažite da opisana kružnica tog trokuta prolazi kroz fokus parabole.
|
Rješenje. Neka je parabola dana formulom y2 = 2px. Tada njen fokus ima koordinate F(p/2, 0). Neka su T1(x1, y1), T2(x2, y2) i T3(x3, y3) tri točke parabole. Apscise tih točaka su xi = yi2 / (2p), a tangente na parabolu kojima su one dirališta imaju jednadžbe ti … y yi = p x + yi2 / 2, za i = 1, 2, 3. Računajući presjeke tangenata t2 ∩ t3, t1 ∩ t3 i t1 ∩ t2 dobivamo koordinate točaka
| A ( | y2 y3 | , | y2 + y3 | ), B ( | y1 y3 | , | y1 + y3 | ) i C ( | y1 y2 | , | y1 + y2 | ). |
| 2p | 2 | 2p | 2 | 2p | 2 |
Središte kružnice opisane trokutu ABC dobijemo kao presjek simetrala stranica AB i AC. Stranice leže na pravcima s koeficijentima smjera kAB = p / y3 i kAC = p / y2, a polovišta su im
| PAB ( | y3 (y1 + y2) | , | y1 + y2 + 2y3 | ) i |
| 4p | 4 | |||
| PAC ( | y2 (y1 + y3) | , | y1 + 2y2 + y3 | ). |
| 4p | 4 |
Sada znamo napisati jednadžbe simetrala stranica
| sAB … y = | −y3 | x + | y32 (y1 + y2) | + | y1 + y2 + 2y3 | , |
| p | 4p2 | 4 |
| sAC … y = | −y2 | x + | y22 (y1 + y3) | + | y1 + 2y2 + y3 | . |
| p | 4p2 | 4 |
Iz ovih dviju jednadžbi odredimo koordinate središta S kružnice opisane trokutu ABC:
| xS = | y1 y2 + y1 y3 + y2 y3 | + | p | , |
| 4p | 4 |
| yS = | y1 + y2 + y3 | − | y1 y2 y3 | . |
| 4 | 4p2 |
Neka je polumjer kružnice R. Možemo izračunati R2 = |AS|2 i provjeriti da vrijedi |SF|2 = R2, iz čega slijedi da fokus F leži na kružnici.
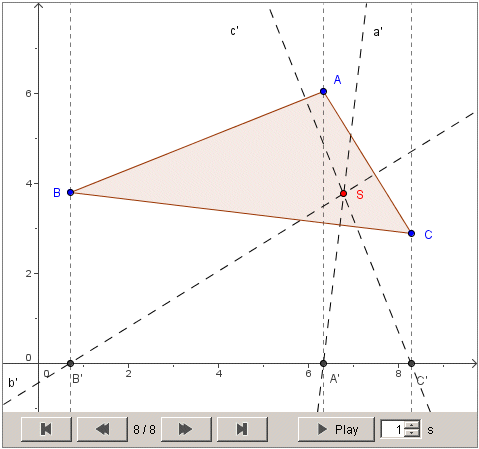
U ravnini je zadan trokut ABC i pravac p. Neka su A', B', C' ortogonalne projekcije točaka A, B, C na pravac p. Dokažite da okomice iz točaka A', B', C' na pravce BC, CA i AB prolaze jednom točkom.
U ovom zadatku bitna je ideja da za pravac p uzmemo x-os. To nam znatno olakšava račun, jer se tada ortogonalna projekcija točke na pravac p dobiva jednostavno izjednačavanjem njezine ordinate s nulom (i ostavljanjem apscise nepromijenjenom).
|
Rješenje. Za pravac p uzimamo da je jednak x-osi. Ako vrhovi zadanog trokuta imaju koordinate A(x1, y1), B(x2, y2) i C(x3, y3), onda su koordinate njihovih ortogonalnih projekcija na pravac p jednake A'(x1, 0), B'(x2, 0) i C'(x3, 0). Koeficijenti smjera pravaca BC, AC i AB redom su
| y3 − y2 | , | y3 − y1 | i | y2 − y1 | . |
| x3 − x2 | x3 − x1 | x2 − x1 |
Koeficijenti smjera okomica na te pravce suprotni su i recipročni. Prema tome, okomice iz točaka A', B' i C' imaju jednadžbe
| a' … | y = − | x3 − x2 | (x −x1), |
| y3 − y2 | |||
| b' … | y = − | x3 − x1 | (x −x2), |
| y3 − y1 | |||
| c' … | y = − | x2 − x1 | (x −x3). |
| y2 − y1 |
Rješavanjem sustava triju linearnih jednadžbi s dvije nepoznanice vidimo da je presjek tih pravaca točka S s koordinatama
| xS = | x1 y1(x3 − x2) + x2 y2(x1 − x3) + x3 y3(x2 − x1) | , |
| x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2) | ||
| yS = | (x3 − x2) (x1 − x3) (x2 − x1) | . |
| x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2) |
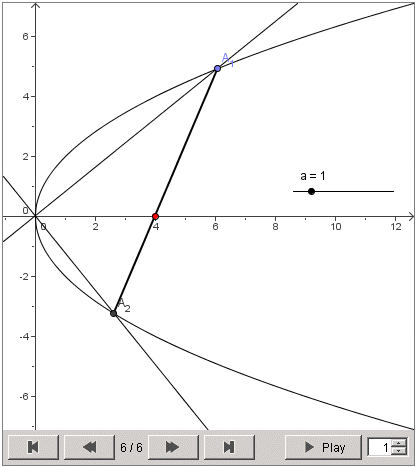
Dokažite da sve tetive parabole y2 = 4ax, koje su hipotenuze pravokutnog trokuta s pravim kutom u ishodištu, prolaze istom točkom.
|
Rješenje. Neka su A1(x1, y1) i A2(x2, y2) krajnje točke tetive parabole. Pravci kroz ishodište i točke A1 i A2 su okomiti. Njihovi koeficijenti smjera su recipročni i suprotni pa vrijedi x1 x2 + y1 y2 = 0. Jednadžba pravca na kojem leži tetiva je oblika y = k x + l. Uvrstimo li taj y u jednadžbu parabole, dobit ćemo kvadratnu jednadžbu koju zadovoljavaju x1 i x2 (apscise presjeka pravca i parabole):
Po Vièteovim formulama dobivamo x1 x2 = l2 / k2. Sada lako izračunamo y1 y2 = 4al / k. Zbrajanjem x1 x2 i y1 y2 i sređivanjem dobivamo l = −4ak. Zaključujemo da svaka tetiva koja je hipotenuza pravokutnog trokuta s vrhom u ishodištu leži na pravcu s jednadžbom oblika y = k(x − 4a), a ti pravci očito prolaze točkom (4a, 0).
| [BE] | E.T. Bell, Veliki matematičari, Znanje, Zagreb, 1972. |
| [B6] | M. Bombardelli, A. Dujella i S. Slijepčević, Matematička natjecanja učenika srednjih škola, Hrvatsko matematičko društvo, Zagreb, 1996. |
| [B7] | M. Bombardelli, Ž. Hanjš i S. Varošanec, Matematička natjecanja 1995./96., Hrvatsko matematičko društvo, Zagreb, 1997. |
| [B8] | M. Bombardelli, I. Brnetić i Ž. Hanjš, Matematička natjecanja 1996./97., Hrvatsko matematičko društvo, Zagreb, 1998. |
| [B9] | M. Bombardelli, A. Čižmešija i Ž. Hanjš, Matematička natjecanja 1997./98., Hrvatsko matematičko društvo, Zagreb, 1999. |
| [B0] | M. Bombardelli, I. Brnetić i Ž. Hanjš, Matematička natjecanja 1998./99., Hrvatsko matematičko društvo, Zagreb, 2000. |
| [B1] | M. Bombardelli, I. Brnetić i Ž. Hanjš, Matematička natjecanja 1999./2000., Hrvatsko matematičko društvo, Zagreb, 2001. |
| [B2] | M. Bombardelli i Ž. Hanjš, Matematička natjecanja 2000./2001., Hrvatsko matematičko društvo, Zagreb, 2002. |
| [B3] | M. Bombardelli, A. Čižmešija i Ž. Hanjš, Matematička natjecanja 2001./2002., Hrvatsko matematičko društvo, Zagreb, 2003. |
| [B4] | M. Bombardelli, Ž. Hanjš i S. Varošanec, Matematička natjecanja 2002./2003., Hrvatsko matematičko društvo, Zagreb, 2004. |
| [B5] | M. Bombardelli, Ž. Hanjš i S. Varošanec, Matematička natjecanja 2003./2004., Hrvatsko matematičko društvo, Zagreb, 2005. |
| [FI] | V. Filipović, Descartes rasprave o metodi, Matica hrvatska, Zagreb, 1951. |
| [JA] | B. Jagodić i R. Svedrec, Matematika 7 za izbornu i dodatnu nastavu, Školske novine, Zagreb, 2000. |
| [KN] | S. Kurepa i L. Neralić, Matematika 3, Udžbenik i zbirka zadataka za treći razred prirodoslovno-matematičke gimnazije, Školska knjiga, Zagreb, 2000. |
| [KU] | Z. Kurnik, René Descartes, Matematika i škola 6 (2000), 26-29. |
| [N5] | Natjecanja: Klokan bez granica, Matka 54 (2005), 119-128. |
| [N6] | Natjecanja: Općinsko-gradsko natjecanje učenika osnovnih škola RH, Matka 56 (2006), 259-266. |
| [ST] | V. Stošić, Natjecanja učenika osnovnih škola, Hrvatsko matematičko društvo, Zagreb, 2000. |
1. Uvod
2. René Descartes
3. Osnovne formule analitičke geometrije
4. Zadaci za osnovnu školu
5. Zadaci za srednju školu
Literatura
Download