
Broj 4























Franka Miriam Brückler
Matematički dvoboji

Sadržaj:
UvodHipasus kontra Pitagore
Tartaglia kontra Cardana
Viète kontra van Roomena
Descartes kontra de Fermata
Newton kontra von Leibniza
Johann kontra Jacoba Bernoullija (i de l'Hôpitala)
Gauss kontra Legendrea
Cauchy kontra mnogih
Kronecker kontra Cantora
Popis literature i linkova

Uvod
Mnoge velike matematičke ideje i dokazi teorema u povijesti nisu prošli glatko, odnosno izazvali su kontroverze unutar svijeta matematičara. Ponekad se radilo o sukobima oko prvenstva ("ja sam to prije dokazao!"), ponekad oko točnosti rezultata ("krivo si to dokazao!"), ponekad oko autorstva ("ukrao si mi teorem!"), a ponekad opet oko smislenosti neke matematičke teorije ("tvoja matematika nema smisla!"). U ovom članku upoznat ćemo se s nekoliko velikih matematičkih ideja u povijesti oko kojih su se razvili takvi sukobi matematičara - ponekad već tada poznati kao sukobi, a ponekad ih možemo iz današnje perspektive takvima zvati...

Hipasus kontra Pitagore
ili: dodekaedar i iracionalnost korijena iz 2 Gotovo svatko čuo je za Pitagoru sa Samosa, nakon Talesa prvog velikog
matematičara u povijesti. No, malo tko je čuo za njegova suvremenika, člana
pitagorejske škole, Hipasusa iz Metaponta.
Pitagora
(oko 570. - 475. pr. Kr.) je u mladosti boravio u Egiptu, a jedno vrijeme i u babilonskom
sužanjstvu. U tim je dvjema zemljama, kao i od svojih učitelja Ferekida, Talesa i Anaksimandra,
naučio osnove matematike. Kad je zbog političkih razloga morao napustiti svoj rodni
otok Samos, u Krotonu u južnoj Italiji oko 518. pr.Kr. osniva svoju znamenitu
pitagorejsku školu.
Radilo se o filozofsko-vjerskoj zajednici koja je zaslužna
za postavljanje danas uobičajenog zahtjeva u matematici da se matematičke
tvrdnje moraju i logički dokazati. Osnovno učenje te škole bilo je da je bit
svega broj - prirodan broj. Stoga su po njihovu shvaćanju jedini dopustivi
brojevi bili prirodni i jedine dopustive veličine one koje se mogu opisati kao
njihovi omjeri (tj. kao racionalni brojevi). Pitagorejci su poznati po nizu
teorema. Navedimo samo neka njihova najvažnija dostignuća: Pitagorin teorem,
osnove teorije brojeva (teorija parnih i neparnih brojeva, savršenih brojeva,
figurativnih brojeva), opis pravilnih poliedara. Dali su i velike doprinose u
astronomiji i glazbi. Kako su pripadnici te škole smatrali Pitagoru božanstvom,
svi su se novi rezultati pripisivali njemu te nije poznato koji su (i jesu li
uopće ikoji) pitagorejski rezultati stvarno Pitagorini.
Gotovo svatko čuo je za Pitagoru sa Samosa, nakon Talesa prvog velikog
matematičara u povijesti. No, malo tko je čuo za njegova suvremenika, člana
pitagorejske škole, Hipasusa iz Metaponta.
Pitagora
(oko 570. - 475. pr. Kr.) je u mladosti boravio u Egiptu, a jedno vrijeme i u babilonskom
sužanjstvu. U tim je dvjema zemljama, kao i od svojih učitelja Ferekida, Talesa i Anaksimandra,
naučio osnove matematike. Kad je zbog političkih razloga morao napustiti svoj rodni
otok Samos, u Krotonu u južnoj Italiji oko 518. pr.Kr. osniva svoju znamenitu
pitagorejsku školu.
Radilo se o filozofsko-vjerskoj zajednici koja je zaslužna
za postavljanje danas uobičajenog zahtjeva u matematici da se matematičke
tvrdnje moraju i logički dokazati. Osnovno učenje te škole bilo je da je bit
svega broj - prirodan broj. Stoga su po njihovu shvaćanju jedini dopustivi
brojevi bili prirodni i jedine dopustive veličine one koje se mogu opisati kao
njihovi omjeri (tj. kao racionalni brojevi). Pitagorejci su poznati po nizu
teorema. Navedimo samo neka njihova najvažnija dostignuća: Pitagorin teorem,
osnove teorije brojeva (teorija parnih i neparnih brojeva, savršenih brojeva,
figurativnih brojeva), opis pravilnih poliedara. Dali su i velike doprinose u
astronomiji i glazbi. Kako su pripadnici te škole smatrali Pitagoru božanstvom,
svi su se novi rezultati pripisivali njemu te nije poznato koji su (i jesu li
uopće ikoji) pitagorejski rezultati stvarno Pitagorini.
 Zanimljivo je da je jedno od
najvećih otkrića pitagorejaca bilo u direktnoj suprotnosti s njihovim
uvjerenjima: radi se o nesumjerljivosti stranice i dijagonale kvadrata.
Za dvije istovrsne geometrijske veličine, npr. dužine, kažemo da su sumjerljive
ako se njihov omjer može izraziti kao omjer prirodnih brojeva. Suvremenim jezikom
rečeno: veličine a i b su sumjerljive ako je a:b
racionalan broj. Danas znamo da je omjer dijagonale D i stranice a
kvadrata jednak kvadratnom korijenu iz 2, koji je iracionalan broj. Ta činjenica
očigledno je u suprotnosti s osnovnim vjerovanjem pitagorejaca da je sve opisivo
pomoću prirodnih brojeva. Danas je uobičajeni dokaz iracionalnosti kvadratnog korijena iz
2 u osnovi pitagorejski, samo što oni nisu posjedovali simbolički zapis, a svoj
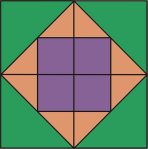
dokaz temelje na kombinaciji geometrije i teorije parnih i neparnih brojeva. Promotrimo
li sliku gore lijevo, koja se sastoji od tri kvadrata, vidimo:
Zanimljivo je da je jedno od
najvećih otkrića pitagorejaca bilo u direktnoj suprotnosti s njihovim
uvjerenjima: radi se o nesumjerljivosti stranice i dijagonale kvadrata.
Za dvije istovrsne geometrijske veličine, npr. dužine, kažemo da su sumjerljive
ako se njihov omjer može izraziti kao omjer prirodnih brojeva. Suvremenim jezikom
rečeno: veličine a i b su sumjerljive ako je a:b
racionalan broj. Danas znamo da je omjer dijagonale D i stranice a
kvadrata jednak kvadratnom korijenu iz 2, koji je iracionalan broj. Ta činjenica
očigledno je u suprotnosti s osnovnim vjerovanjem pitagorejaca da je sve opisivo
pomoću prirodnih brojeva. Danas je uobičajeni dokaz iracionalnosti kvadratnog korijena iz
2 u osnovi pitagorejski, samo što oni nisu posjedovali simbolički zapis, a svoj
dokaz temelje na kombinaciji geometrije i teorije parnih i neparnih brojeva. Promotrimo
li sliku gore lijevo, koja se sastoji od tri kvadrata, vidimo:
- ako je stranica srednjeg kvadrata sumjerljiva dijagonali, one imaju omjer kao dva prirodna broja n i m (tj. stranica je oblika nd, a dijagonala oblika md za neku dužinu d);
- kad bi oba broja m i n bila parna, umjesto d možemo uzeti 2d pa pretpostavimo da nisu oba parna;
- površina velikog kvadrata dvostruka je površina srednjeg, dakle m2d2=2n2d2, iz čega slijedi da je m paran jer je paran kvadratni broj četverostruki kvadratni (drugim riječima: ako je N2 paran, onda je N paran);
- slijedi da je md=2kd za neki prirodan broj k;
- površina srednjeg kvadrata dvostruka je površina malog, pa je n2d2=2k2d2, iz čega kao gore slijedi da je i n paran;
- ispada da smo dobili kontradikciju s pretpostavkom, dakle nije istina da su stranica i dijagonala kvadrata sumjerljive.
 Vjerojatno prva osoba koja je dala gornji dokaz bio je Hipasus iz Metaponta,
Pitagorin učenik. O njemu se također malo zna, ali ima više legendi o njegovoj smrti.
Prema jednoj, zbog otkrića postojanja "zabranjenih" nesumjerljivih veličina pitagorejci
su ga izbacili iz broda te se utopio. Prema drugoj legendi, to se dogodilo jer nije
Pitagori pripisao otkriće
dodekaedra, odnosno utopio se jer su ga
"kaznili bogovi". Prilično sigurno jest da je Hipasus bio izopćen iz pitagorejske škole
zbog suprotstavljanja nekim idejama pitagorejaca, te su mu još za života izradili grob.
Vjerojatno prva osoba koja je dala gornji dokaz bio je Hipasus iz Metaponta,
Pitagorin učenik. O njemu se također malo zna, ali ima više legendi o njegovoj smrti.
Prema jednoj, zbog otkrića postojanja "zabranjenih" nesumjerljivih veličina pitagorejci
su ga izbacili iz broda te se utopio. Prema drugoj legendi, to se dogodilo jer nije
Pitagori pripisao otkriće
dodekaedra, odnosno utopio se jer su ga
"kaznili bogovi". Prilično sigurno jest da je Hipasus bio izopćen iz pitagorejske škole
zbog suprotstavljanja nekim idejama pitagorejaca, te su mu još za života izradili grob.


Tartaglia kontra Cardana
ili: kako riješiti kubnu jednadžbu?U današnje vrijeme svi u školi uče kako riješiti linearnu i kvadratnu jednadžbu, a ta rješenja (iako ne u suvremenom obliku zapisa) bila su poznata još u jako davna vremena Babilonaca. Za razliku od tih jednadžbi, kubne jednadžbe i jednadžbe višeg stupnja doduše se spominju, ali se formule i postupci za njihovo rješavanje opisuju samo za slučaje kad se jednadžba (točnije: polinom kojem u toj jednadžbi tražimo nultočke) može "lijepo" faktorizirati, npr. x3-4x=0 je x(x-2)(x+2)=0. Mnogi zbog toga misle da ne postoje formule za rješenje kubne jednadžbe. No one postoje, čak i za jednadžbu četvrtog stupnja, samo su jako komplicirane te nepogodne za pamćenje. Te su formule, točnije rečeno postupke kojima se one izvode, otkrili talijanski renesansni matematičari Scipione del Ferro, Niccolo Tartaglia, Girolamo Cardano i Lodovico Ferrari.
Matematičari renesanse znaju da se svaka kubna jednadžba može svesti na oblik bez kvadratnog člana putem linearne supstitucije (početnu varijablu x zamijenimo s y koji je jednak x umanjenom za trećinu koeficijenta uz kvadratni član). Stoga je dovoljno znati riješiti jednadžbe oblika x3+px+q=0. Napomenimo još i da u renesansi, iako su ponegdje poznati, negativni brojevi još nisu općeprihvaćeni te su stoga u renesansnom shvaćanju jednadžbe x3+px=q i x3=px+q različiti tipovi kubne jednadžbe.
Scipione del Ferro oko 1515. rješava prvi tip kubne jednadžbe, no svoj postupak drži u tajnosti. Tek na samrti (1526.) odaje ga svom zetu Hanibalu Naveu i učeniku Antoniju Fioru, koji je bio osrednji matematičar i u poznavanju tajne metode vidio je šansu da dođe do slave i novca. Fior se počinje hvaliti znanjem rješavanja kubne jednadžbe spomenutog tipa te se širi vijest da je ona riješena. I sad u priču ulazi Tartaglia ...
 Niccolo
Tartaglia (1499.-1557.) bio je samouki matematičar iz Brescie. Tartaglia znači mucavac,
a taj je nadimak dobio zbog govorne mane koja je bila posljedica ozljede u djetinjstvu: kad su
Francuzi osvojili njegovu rodnu Bresciu, jedan mu je vojnik mačem rasjekao čeljust: Niccolo
je jedva ostao živ, a posljedica je bila nakaznost zbog koje je stalno nosio bradu,
te spomenuta govorna mana. Kako je bio iz vrlo siromašne obitelji, školovao se potpuno sam.
Već dosta rano razvio je velike matematičke sposobnosti i zarađivao za život predajući
matematiku u Veroni i Veneciji. 1530-ih godina otkriva metodu za rješenje jednadžbe tipa
x3+px2=q i ne taji svoje otkriće. Kako je Fior
bio uvjeren da samo on zna riješiti tip x3+px=q, on izaziva
Tartagliu na natjecanje (1535.) na kojem svaki treba zadati drugome po 30 zadataka s
rokom rješavanja od 50 dana. Tartaglia je očekivao da će mu Fior zadati jednadžbe tipa
x3+px=q te na brzinu smišlja metodu njihova rješavanja.
Kad je došao dan natjecanja, njegovo očekivanje pokazalo se točnim:
Fior je njemu zadao zadatke isključivo tog tipa te ih je Tartaglia sve riješio za dva sata.
Nasuprot tome, Tartaglia je Fioru zadao razne zadatke, od kojih neke i "svog" tipa,
koje Fior nije uspio riješiti.
Niccolo
Tartaglia (1499.-1557.) bio je samouki matematičar iz Brescie. Tartaglia znači mucavac,
a taj je nadimak dobio zbog govorne mane koja je bila posljedica ozljede u djetinjstvu: kad su
Francuzi osvojili njegovu rodnu Bresciu, jedan mu je vojnik mačem rasjekao čeljust: Niccolo
je jedva ostao živ, a posljedica je bila nakaznost zbog koje je stalno nosio bradu,
te spomenuta govorna mana. Kako je bio iz vrlo siromašne obitelji, školovao se potpuno sam.
Već dosta rano razvio je velike matematičke sposobnosti i zarađivao za život predajući
matematiku u Veroni i Veneciji. 1530-ih godina otkriva metodu za rješenje jednadžbe tipa
x3+px2=q i ne taji svoje otkriće. Kako je Fior
bio uvjeren da samo on zna riješiti tip x3+px=q, on izaziva
Tartagliu na natjecanje (1535.) na kojem svaki treba zadati drugome po 30 zadataka s
rokom rješavanja od 50 dana. Tartaglia je očekivao da će mu Fior zadati jednadžbe tipa
x3+px=q te na brzinu smišlja metodu njihova rješavanja.
Kad je došao dan natjecanja, njegovo očekivanje pokazalo se točnim:
Fior je njemu zadao zadatke isključivo tog tipa te ih je Tartaglia sve riješio za dva sata.
Nasuprot tome, Tartaglia je Fioru zadao razne zadatke, od kojih neke i "svog" tipa,
koje Fior nije uspio riješiti.
 Za Tartagliinu pobjedu saznao je milanski liječnik, matematičar i kockar
Girolamo
Cardano (1501.-1576.), jedna od najneobičnijih ličnosti matematičke povijesti.
Cardano je živio burno. Kao liječnik bio je toliko znamenit da je na zahtjev nadbiskupa iz
Edinburgha putovao u Škotsku da ga izliječi. Kao matematičar razvija niz novih ideja i
zbog svog interesa za kockanje dolazi do osnovnih elemenata teorije vjerojatnosti. Često živi
na rubu moralnog i dopustivog, a oba sina su mu kriminalci. Stariji će biti smaknut
pod inkvizicijom jer je otrovao ženu, a mlađi je kao i otac ovisnik o kocki te zbog toga
pribjegava krađi. I sam Cardano u jednom je navratu završio u inkvizicijskom zatvoru
jer je izradio horoskop Isusa Krista, no brzo biva oslobođen zbog dobrih veza s papinskim
dvorom. Prema legendi, umro je počinivši samoubojstvo kako bi potvrdio da je točno prorekao datum
svoje smrti.
Za Tartagliinu pobjedu saznao je milanski liječnik, matematičar i kockar
Girolamo
Cardano (1501.-1576.), jedna od najneobičnijih ličnosti matematičke povijesti.
Cardano je živio burno. Kao liječnik bio je toliko znamenit da je na zahtjev nadbiskupa iz
Edinburgha putovao u Škotsku da ga izliječi. Kao matematičar razvija niz novih ideja i
zbog svog interesa za kockanje dolazi do osnovnih elemenata teorije vjerojatnosti. Često živi
na rubu moralnog i dopustivog, a oba sina su mu kriminalci. Stariji će biti smaknut
pod inkvizicijom jer je otrovao ženu, a mlađi je kao i otac ovisnik o kocki te zbog toga
pribjegava krađi. I sam Cardano u jednom je navratu završio u inkvizicijskom zatvoru
jer je izradio horoskop Isusa Krista, no brzo biva oslobođen zbog dobrih veza s papinskim
dvorom. Prema legendi, umro je počinivši samoubojstvo kako bi potvrdio da je točno prorekao datum
svoje smrti.
Cardano je, dakle, saznao za nove događaje vezane uz rješavanje tada iznimno popularnog problema kubne jednadžbe, kojim se i sam bavio. On poziva Tartagliu da mu oda svoj postupak, no Tartaglia odbija. Slijedilo je Cardanovo uvjeravanje te on konačno uspijeva nagovoriti Tartagliu da ga posjeti, obećavši mu da će ga upoznati sa zapovjednikom vojske u Milanu, koji bi Tartaglii mogao priskrbiti bolji posao. Tartaglia po dolasku u Milano saznaje da je spomenuti zapovjednik odsutan, no Cardano iz njega uspijeva izvući metodu rješenja kubne jednadžbe. Tartaglia ju je odao u stihu i samo uz uvjet da se Cardano zakune da je neće objaviti sve dok je on, Tartaglia, sam ne objavi. Stih je, u slobodnom prijevodu, glasio ovako:
Kad su kub i stvari skupa
Jednaki nekom diskretnom broju
Nađi druga dva broja
Koji se za taj razlikuju
Tad ćeš to zadržati kao naviku
Da im je produkt uvijek jednak
Točno kubu trećine od stvari
Ostatak tad kao opće pravilo
Od njihovih oduzetih kubnih korijena
Bit će jednak tvojoj osnovnoj stvari.
Za današnji jezik zbunjujući pojam "stvari" samo je tada uobičajena riječ res kao oznaka nepoznanice. Uz malu koncentraciju, vidi se da se radi o uputi za rješavanje kubne jednadžbe bez kvadratnog člana x3+px=q. Uputa kaže da treba riješiti sustav u-v=q, 27uv=p3 te se rješenje polazne jednadžbe x dobiva kao razlika kubnih korijena iz u i v.
Iz Tartaglinog rješenja Cardano sa svojim studentom Lodovicom Ferrarijem razvija metodu koja je primjenjiva za oba tipa kubnih jednadžbi, a Ferrari iz nje dalje izvodi i metodu za rješenje jednadžbe četvrtog stupnja. Kad Cardano saznaje da Tartaglia nije prvi koji je razvio tu metodu, odlučuje objaviti svoje najznamenitije djelo Ars Magna (1545.). U njemu daje detaljni opis metode za jednadžbe trećeg i četvrtog stupnja i pritom navodi Tartagliu kao autora metode koju je od njega dobio. No, Tartaglia - koji u desetak godina koliko je prošlo od sastanka s Cardanom još nije objavio svoju metodu - je razbješnjen kršenjem zakletve. On objavljuje svoju verziju priče i izaziva Cardana na natjecanje koje se također održalo u Milanu. Cardano na to natjecanje šalje Ferrarija, koji je bio zadužen i za javnu obranu Cardana, a on Tartagliu glatko pobjeđuje. Tartaglia je morao otići s natjecanja, po nekim izvorima pobjegao je iz grada pod zaštitom mraka, po drugima je jedva izvukao živu glavu, a sigurno je da je Tartaglia tim natjecanjem izgubio i slavu i prihod. Danas su pak iz Cardanova opisa u djelu Ars Magna izvedene formule za rješenje kubne jednadžbe, poznate kao Cardanove ili Cardano-Tartagliine formule.

Viète kontra van Roomena
ili: matematika u diplomaciji Za daljnji razvoj
algebre tijekom renesanse
osobito je zaslužan znameniti francuski matematičar koji to nije bio:
François
Viète (1540.-1603.) po struci je bio pravnik. Veći dio života proveo
je na raznim državnim dužnostima - bio je zastupnik u francuskom parlamentu i savjetnik
kraljeva Henrika III. i IV. u burno doba kontrareformacije. Kao matematičar iz hobija,
dvaput se
našao u prilici pomoći svojoj državi znanjem matematike.
Za daljnji razvoj
algebre tijekom renesanse
osobito je zaslužan znameniti francuski matematičar koji to nije bio:
François
Viète (1540.-1603.) po struci je bio pravnik. Veći dio života proveo
je na raznim državnim dužnostima - bio je zastupnik u francuskom parlamentu i savjetnik
kraljeva Henrika III. i IV. u burno doba kontrareformacije. Kao matematičar iz hobija,
dvaput se
našao u prilici pomoći svojoj državi znanjem matematike.
 Prvi put
bilo je to kad je španjolski
kralj Filip II., poznati
borac protiv reformacije, zagovornik inkvizicije i pokretač armade
protiv Engleske, 1590. godine postavio zahtjev za francuskim prijestoljem na osnovi rodbinskih
veza. Tadašnji francuski kralj
Henrik IV., protestant, odbija zahtjeve te dolazi do rata.
U tom ratu slane su razne šifrirane poruke te iz tog doba potječe jedna od
najpoznatijih matematičkih anegdota iz kriptografije. Francuzi su presreli jednu španjolsku
poruku te ju je kralj dao Vièteu da je dešifrira. To Viète i uspijeva,
Španjolcima postaje jasno da Francuzi znaju za njihove namjere, a Filip II.
tužio je Francusku papi da se koristi crnom magijom...
Prvi put
bilo je to kad je španjolski
kralj Filip II., poznati
borac protiv reformacije, zagovornik inkvizicije i pokretač armade
protiv Engleske, 1590. godine postavio zahtjev za francuskim prijestoljem na osnovi rodbinskih
veza. Tadašnji francuski kralj
Henrik IV., protestant, odbija zahtjeve te dolazi do rata.
U tom ratu slane su razne šifrirane poruke te iz tog doba potječe jedna od
najpoznatijih matematičkih anegdota iz kriptografije. Francuzi su presreli jednu španjolsku
poruku te ju je kralj dao Vièteu da je dešifrira. To Viète i uspijeva,
Španjolcima postaje jasno da Francuzi znaju za njihove namjere, a Filip II.
tužio je Francusku papi da se koristi crnom magijom...
 Druga prilika da se Viète iskaže u matematičkoj diplomaciji vezana je uz tematiku ovog
članka. Godine 1593. belgijski matematičar
Adriaan
van Roomen (Adrianus Romanus, 1561.-1615.)
zadaje zadatak s jednadžbom stupnja 45. Tadašnji nizozemski ambasador u Francuskoj izjavljuje da
Francuska nema dovoljno dobrih matematičara da riješe van Roomenov problem te ga
kralj Henrik IV. daje Vièteu. On ga je riješio uočivši da se radi u biti
o trigonometrijskoj relaciji (vezanoj uz formulu koju danas poznajemo kao de Moivreovu), te je
time spašen ugled francuskih matematičara. Za razliku od ostalih "dvoboja" opisanih u
ovom članku, ovaj je završio harmonično: Viète i van Roomen postali su prijatelji.
Druga prilika da se Viète iskaže u matematičkoj diplomaciji vezana je uz tematiku ovog
članka. Godine 1593. belgijski matematičar
Adriaan
van Roomen (Adrianus Romanus, 1561.-1615.)
zadaje zadatak s jednadžbom stupnja 45. Tadašnji nizozemski ambasador u Francuskoj izjavljuje da
Francuska nema dovoljno dobrih matematičara da riješe van Roomenov problem te ga
kralj Henrik IV. daje Vièteu. On ga je riješio uočivši da se radi u biti
o trigonometrijskoj relaciji (vezanoj uz formulu koju danas poznajemo kao de Moivreovu), te je
time spašen ugled francuskih matematičara. Za razliku od ostalih "dvoboja" opisanih u
ovom članku, ovaj je završio harmonično: Viète i van Roomen postali su prijatelji.

Descartes kontra de Fermata
ili: kako naći tangentu? Veliki filozof i matematičar
René
Descartes (1596.-1650.) u povijesti matematike
najpoznatiji je po svom otkriću analitičke geometrije, točnije mogućnosti da točke ravnine prikazujemo
kao uređene parove realnih brojeva, što omogućuje algebarski pristup geometrijskim problemima.
Manje je poznato da je neovisno o njemu u isto vrijeme (1630-ih godina) analitičku geometriju otkrio i
Pierre
de Fermat (1601.-1665.), francuski pravnik i matematičar iz hobija koji je ostao najpoznatiji
po velikom Fermatovom teoremu, tek nedavno dokazanom. Veliki Fermatov teorem tvrdi da za
prirodne n>2 jednadžba
Veliki filozof i matematičar
René
Descartes (1596.-1650.) u povijesti matematike
najpoznatiji je po svom otkriću analitičke geometrije, točnije mogućnosti da točke ravnine prikazujemo
kao uređene parove realnih brojeva, što omogućuje algebarski pristup geometrijskim problemima.
Manje je poznato da je neovisno o njemu u isto vrijeme (1630-ih godina) analitičku geometriju otkrio i
Pierre
de Fermat (1601.-1665.), francuski pravnik i matematičar iz hobija koji je ostao najpoznatiji
po velikom Fermatovom teoremu, tek nedavno dokazanom. Veliki Fermatov teorem tvrdi da za
prirodne n>2 jednadžba
 Sukob započinje kad je de Fermat ustvrdio da Descartes 1637. nije točno izveo zakon
loma svjetlosti. Na taj se prigovor Descartes vrlo razljutio, osobito kad je otkrio da
de Fermatovi rezultati o tangentama i ekstremima umanjuju važnost njegovog
za matematiku najznačajnijeg djela, La Géométrie, na koje je
bio osobito ponosan. Tada Descartes napada
de Fermatovu metodu i kako je sukob eskalirao, u njega su uključeni i drugi matematičari,
poput Robervala i Étienne Pascala (oca Blaisea Pascala). Descartes je zamolio
Girarda
Desarguesa da presudi tko je u pravu. Napomenimo da su svi oni (Descartes, Desargues, É.
Pascal, Roberval) bili članovi Mersenneovog kruga, skupine tada najboljih francuskih matematičara
okupljenih oko Marina Mersennea.
Desargues u sukobu Descartes-Fermat utvrđuje da je de Fermat u pravu, na što
Descartes komentira: ... kad sam vidio posljednju metodu koju koristite za nalaženje
tangenti na krivulje, ne mogu drugačije odgovoriti nego tako da kažem da je vrlo dobra
i da ste je ovako objasnili na početku, ne bih joj se suprotstavljao. Ipak, Descartes je i nakon toga
pokušavao oštetiti de Fermatovu reputaciju: tako je npr. pohvalno pisao Fermatu o njegovoj
(točnoj) metodi određivanja tangente na cikloidu, a istovremeno pisao i Mersenneu da metoda nije točna
te da je de Fermat nesposoban kao matematičar i mislilac.
Sukob započinje kad je de Fermat ustvrdio da Descartes 1637. nije točno izveo zakon
loma svjetlosti. Na taj se prigovor Descartes vrlo razljutio, osobito kad je otkrio da
de Fermatovi rezultati o tangentama i ekstremima umanjuju važnost njegovog
za matematiku najznačajnijeg djela, La Géométrie, na koje je
bio osobito ponosan. Tada Descartes napada
de Fermatovu metodu i kako je sukob eskalirao, u njega su uključeni i drugi matematičari,
poput Robervala i Étienne Pascala (oca Blaisea Pascala). Descartes je zamolio
Girarda
Desarguesa da presudi tko je u pravu. Napomenimo da su svi oni (Descartes, Desargues, É.
Pascal, Roberval) bili članovi Mersenneovog kruga, skupine tada najboljih francuskih matematičara
okupljenih oko Marina Mersennea.
Desargues u sukobu Descartes-Fermat utvrđuje da je de Fermat u pravu, na što
Descartes komentira: ... kad sam vidio posljednju metodu koju koristite za nalaženje
tangenti na krivulje, ne mogu drugačije odgovoriti nego tako da kažem da je vrlo dobra
i da ste je ovako objasnili na početku, ne bih joj se suprotstavljao. Ipak, Descartes je i nakon toga
pokušavao oštetiti de Fermatovu reputaciju: tako je npr. pohvalno pisao Fermatu o njegovoj
(točnoj) metodi određivanja tangente na cikloidu, a istovremeno pisao i Mersenneu da metoda nije točna
te da je de Fermat nesposoban kao matematičar i mislilac.
U čemu se sastojao problem oko boljeg rješenja kojeg su se sukobili de Fermat i Descartes? Trebalo je odrediti metodu pomoću koje je na poznatu krivulju moguće nacrtati tangentu u nekoj njezinoj točki. Uz to je usko vezan problem određivanja ekstrema, tj. minimuma i maksimuma funkcije, jer se ekstremi postižu u onim točkama krivulje (nacrtane u koordinatnoj ravnini) u kojima je tangenta horizontalna (ovo vrijedi ako je krivulja glatka, tj. "lijepo zaobljena", bez šiljaka i prekida). U to doba uobičajena definicija tangente bila je da se radi o pravcu kroz točku na krivulji tako da se između njega i krivulje ne može nacrtati drugi pravac. Descartes predlaže novu definiciju da je tangenta granični položaj sekante (tj. pravca kroz dvije točke krivulje) kad su te točke vrlo blizu. Tu će definiciju prihvatiti i de Fermat, a i kasnije npr. Lagrange. Uz te definicije pojavile su se i neke druge, koje se u biti sve svode na isto, no svejedno su izazvale živu raspravu u matematičkim krugovima. Kao metodu za određivanje tangente Descartes predlaže da se odredi središte i polumjer kružnice koja se u danoj točki krivulje "priljubljuje" uz krivulju, a zatim odredi tangenta na kružnicu. Tu je metodu primjenjivao samo na krivulje koje imaju os simetrije pa je traženo središte kružnice na toj osi. Više detalja o Descartesovoj metodi možete naći putem prethodnog i idućeg linka za metodu određivanja tangente.
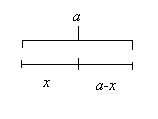 De Fermatova metoda za određivanje tangente
i time ekstrema bila je u biti ista kao kasnija Newtonova
i von Leibnizova, kojom su utemeljili postupak deriviranja. Za određivanje npr. maksimuma de Fermat varijablu
x zamjenjuje s x+e, gdje je e jako mali pozitivan broj. Nakon toga bi izjednačio polaznu i novu
ovisnost te pokratio e-dijelove. Npr. ako na dužini duljine a tražimo točku takvu da je
produkt njezinih udaljenosti do oba kraja (x i a-x) maksimalan, imamo redom:
De Fermatova metoda za određivanje tangente
i time ekstrema bila je u biti ista kao kasnija Newtonova
i von Leibnizova, kojom su utemeljili postupak deriviranja. Za određivanje npr. maksimuma de Fermat varijablu
x zamjenjuje s x+e, gdje je e jako mali pozitivan broj. Nakon toga bi izjednačio polaznu i novu
ovisnost te pokratio e-dijelove. Npr. ako na dužini duljine a tražimo točku takvu da je
produkt njezinih udaljenosti do oba kraja (x i a-x) maksimalan, imamo redom:
x (a - x)=(x + e) (a - x - e)
ax - x2=ax - x2 + ea - 2ex - e2
ea= 2ex + e2
a= 2x + e.
Kako je e jako mali, znači da je x=0,5a.
 Iako de Fermat nije nikad potpuno precizirao ni formalizirao svoju metodu,
ona je u biti današnja definicija
derivacije: gornji postupak odredio je x takav da je za njega derivacija funkcije
f(x)=x(a-x) jednaka nuli, tj. da je za taj x tangenta na graf te funkcije paralelna s x-osi.
Pomoću svog malog prirasta e, koji je kad dijelimo s njim, različit od 0,
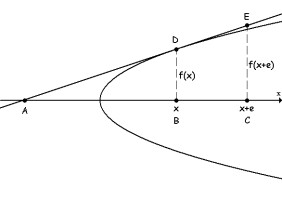
ali kad ostane "sam", zanemariv je,tj. izjednačen s 0, de Fermat je izveo i metodu za određivanje tangente. Da bi odredio tangentu u točki
krivulje s apscisom x, on gleda i točku s apscisom x+e
(dakle, sasvim malo desno od prve točke), kao na slici lijevo. Tada su trokuti ABD i ACE slični pa ako
sa s označimo udaljenost od A do B, imamo
s/(s+e)=f(x)/f(x+e).
Iz tog se izračuna da je
s=ef(x)/[f(x+e)-f(x)].
Kad se uvrsti konkretna jednadžba
krivulje, pokrati e te preostali e izjednači s 0, dobije se
približna vrijednost od s, tj. pozicija točke
A u odnosu na B ako želimo tangentu u D. Konkretno, za krivulju
f(x)=x3 dobije se
s=ex3/[(x+e)3-x3]=
ex3/(3ex2+3xe2+e3)=
x3/(3x2+3xe+e2)=
x3/(3x2)=x/3.
Iako de Fermat nije nikad potpuno precizirao ni formalizirao svoju metodu,
ona je u biti današnja definicija
derivacije: gornji postupak odredio je x takav da je za njega derivacija funkcije
f(x)=x(a-x) jednaka nuli, tj. da je za taj x tangenta na graf te funkcije paralelna s x-osi.
Pomoću svog malog prirasta e, koji je kad dijelimo s njim, različit od 0,
ali kad ostane "sam", zanemariv je,tj. izjednačen s 0, de Fermat je izveo i metodu za određivanje tangente. Da bi odredio tangentu u točki
krivulje s apscisom x, on gleda i točku s apscisom x+e
(dakle, sasvim malo desno od prve točke), kao na slici lijevo. Tada su trokuti ABD i ACE slični pa ako
sa s označimo udaljenost od A do B, imamo
s/(s+e)=f(x)/f(x+e).
Iz tog se izračuna da je
s=ef(x)/[f(x+e)-f(x)].
Kad se uvrsti konkretna jednadžba
krivulje, pokrati e te preostali e izjednači s 0, dobije se
približna vrijednost od s, tj. pozicija točke
A u odnosu na B ako želimo tangentu u D. Konkretno, za krivulju
f(x)=x3 dobije se
s=ex3/[(x+e)3-x3]=
ex3/(3ex2+3xe2+e3)=
x3/(3x2+3xe+e2)=
x3/(3x2)=x/3.

Newton kontra von Leibniza
ili: tko je otkrio infinitezimalni račun?
 Sigurno najpoznatiji sukob u povijesti matematike bio je između sir
Isaaca Newtona
(1643.-1727., slika lijevo) i Gottfireda Wilhelma von Leibniza (1646.-1716., slika desno)
oko otkrića infinitezimalnog računa.
Newtonovi doprinosi fizici i matematici iznimni su, a među najpoznatijima
je njegova univerzalna teorija gravitacije. Tijekom svoje karijere obavljao je i važne
političke
dužnosti, a dugo vremena (1703.-1727.) bio je predsjednik uglednog znanstvenog društva
Royal Society. Von Leibniz je pak najpoznatiji po svojoj filozofiji i težnji k objedinjavanju
znanosti i nalaženju univerzalnog jezika za sve znanosti.
Sigurno najpoznatiji sukob u povijesti matematike bio je između sir
Isaaca Newtona
(1643.-1727., slika lijevo) i Gottfireda Wilhelma von Leibniza (1646.-1716., slika desno)
oko otkrića infinitezimalnog računa.
Newtonovi doprinosi fizici i matematici iznimni su, a među najpoznatijima
je njegova univerzalna teorija gravitacije. Tijekom svoje karijere obavljao je i važne
političke
dužnosti, a dugo vremena (1703.-1727.) bio je predsjednik uglednog znanstvenog društva
Royal Society. Von Leibniz je pak najpoznatiji po svojoj filozofiji i težnji k objedinjavanju
znanosti i nalaženju univerzalnog jezika za sve znanosti.
 Newton je svoje prve rezultate o fluksijama dobio u razdoblju 1665.-1671.,
no prvi put ih je objavio tek
1736. Fluksije su brzine fluensa x i y, a fluensi su veličine ovisne o vremenu
(koordinate točke koja se giba u ravnini po nekoj krivulji). Newtonova varijanta infinitezimalnog
računa sastojala se u određivanju koeficijenta smjera tangente na krivulju po kojoj se točka giba
(tj. omjera vertikalne i horizontalne brzine) pomoću infinitezimalnog (beskonačno malog) prirasta
o slično kao u de Fermatovoj metodi određivanja tangenti i ekstrema. Newton je uočio da
je problemu određivanja tangente iz poznavanja fluensa inverzan problem određivanja vertikalnog
fluensa (tj. vrijednosti funkcije y) iz koeficijenta smjera tangente i horizontalnog fluensa. Time
je dobio osnovni teorem infinitezimalnog računa: deriviranje (određivanje koeficijenta smjera tangente na
krivulju, tj. brzine iz puta) i integriranje (određivanje puta iz brzine) međusobno su inverzne operacije.
Ekvivalentne rezultate, ali u drugom obliku, dobio je von Leibniz 1672. Von Leibniz će
vrlo brzo razviti danas uobičajenu notaciju ydx
i prvi put je koristi u rukopisu 1675. Što se samog računa tiče, njegov dx je isto što i infinitezimalni prirasti e kod
de Fermata, odnosno o kod Newtona, no u daljnjem razvoju računa ova notacija,
koja ističe veličinu čiji prirast gledamo, ima niz prednosti. Godine 1673. posjetio je
London te je tada možda imao priliku vidjeti Newtonove rukopise.
Nakon što je von Leibniz objavio svoje rezultate, Newton mu piše o svojima, koje još nije
objavio, no bez opisa svoje metode. To pismo je dugo putovalo te se brz von Leibnizov odgovor
nije takvim činio Newtonu. Von Leibniz odlučuje što prije objaviti ostatak svojih rezultata, a
Newton 1676. piše drugo pismo, koje je putovalo više od pola godine. U tom pismu Newton
tvrdi da mu je von Leibniz ukrao metodu, a u odgovoru na njega von Leibniz daje neke detalje svoje
metode. Von Leibniz je svoju varijantu izveo iz promatranja redova, uočivši da je za dani niz kojemu
tražimo zbroj y0+y1+y2+...+yn
lako naći zbroj diferencija
di=yi-yi -1
uzastopnih članova niza:
d1+d2+...+dn=yn-y0.
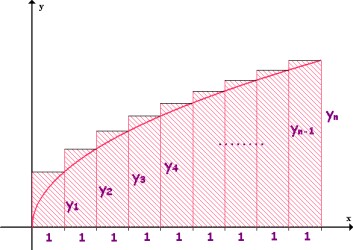
Kad se, kao na slici gore desno, promatra površina ispod neke krivulje, možemo je aproksimirati
zbrojem njezinih ordinata yi u razmacima od po 1 jer su površine pravokutnika
jednake yi·1. Što je odabrana jedinica 1 manja,
to je zbroj tih površina
y1+y2+...+yn bliži
stvarnoj površini ispod krivulje. Budući da su razmaci između dva susjedna x-a jednaki
xi+1-xi=1,
slijedi da je koeficijent smjera sekante između dviju
susjednih (u smislu pomaka apscise za 1) točaka na grafu jednak
(yi+1-yi)/(xi+1-xi)=
yi+1-yi, tj. koeficijent smjera sekante je diferencija
niza y-a koji želimo zbrojiti. Također, što je odabrana jedinica 1 manja, to je koeficijent smjera
sekante bliži koeficijentu smjera tangente u lijevoj od dviju susjednih točaka.
Ako se odabrana jedinica 1 prozove dx, površina je jednaka zbroju izraza oblika ydx (za x
u određenim granicama), a koeficijent smjera tangente jednak je dy/dx, gdje je dy promjena
y ako se x promijeni za dx
(tj. dy je diferencija uzastopnih članova niza y-a).
Uočimo da je, za razliku od Newtona, von Leibniz
kao koeficijent smjera tangente dobio ne omjer fluksija, tj. brzina, nego omjer infinitezimalnih
prirasta osnovnih veličina (koje bi Newton zvao fluensi). S obzirom na vezu između zbrajanja niza i
njegova niza diferencija, von Leibniz zaključuje da inverznost tih operacija vrijedi i kad su razmaci
među članovima infinitezimalni, tj. zaključuje da su postupci integriranja i deriviranja međusobno inverzni,
dakle traženje koeficijenta smjera tangente i površine ispod krivulje međusobno su inverzni postupci.
Tako nakon par godina isprobavanja označavanja kako bi bilo što konzistentnije, von Leibniz dolazi do
i danas smislene notacije d∫dy=ydx.
Napomenimo
da su i ranije postojale metode integriranja tj. nalaženja površine (npr. starogrčka metoda ekshaustije)
te nalaženja tangente (npr. Descartesova i de Fermatova metoda), no razlog zašto se otkriće
infinitezimalnog računa pripisuje Newtonu i von Leibnizu jest njihovo otkriće osnovnog teorema
infinitezimalnog računa, tj. veze između tih dvaju postupaka.
Newton je svoje prve rezultate o fluksijama dobio u razdoblju 1665.-1671.,
no prvi put ih je objavio tek
1736. Fluksije su brzine fluensa x i y, a fluensi su veličine ovisne o vremenu
(koordinate točke koja se giba u ravnini po nekoj krivulji). Newtonova varijanta infinitezimalnog
računa sastojala se u određivanju koeficijenta smjera tangente na krivulju po kojoj se točka giba
(tj. omjera vertikalne i horizontalne brzine) pomoću infinitezimalnog (beskonačno malog) prirasta
o slično kao u de Fermatovoj metodi određivanja tangenti i ekstrema. Newton je uočio da
je problemu određivanja tangente iz poznavanja fluensa inverzan problem određivanja vertikalnog
fluensa (tj. vrijednosti funkcije y) iz koeficijenta smjera tangente i horizontalnog fluensa. Time
je dobio osnovni teorem infinitezimalnog računa: deriviranje (određivanje koeficijenta smjera tangente na
krivulju, tj. brzine iz puta) i integriranje (određivanje puta iz brzine) međusobno su inverzne operacije.
Ekvivalentne rezultate, ali u drugom obliku, dobio je von Leibniz 1672. Von Leibniz će
vrlo brzo razviti danas uobičajenu notaciju ydx
i prvi put je koristi u rukopisu 1675. Što se samog računa tiče, njegov dx je isto što i infinitezimalni prirasti e kod
de Fermata, odnosno o kod Newtona, no u daljnjem razvoju računa ova notacija,
koja ističe veličinu čiji prirast gledamo, ima niz prednosti. Godine 1673. posjetio je
London te je tada možda imao priliku vidjeti Newtonove rukopise.
Nakon što je von Leibniz objavio svoje rezultate, Newton mu piše o svojima, koje još nije
objavio, no bez opisa svoje metode. To pismo je dugo putovalo te se brz von Leibnizov odgovor
nije takvim činio Newtonu. Von Leibniz odlučuje što prije objaviti ostatak svojih rezultata, a
Newton 1676. piše drugo pismo, koje je putovalo više od pola godine. U tom pismu Newton
tvrdi da mu je von Leibniz ukrao metodu, a u odgovoru na njega von Leibniz daje neke detalje svoje
metode. Von Leibniz je svoju varijantu izveo iz promatranja redova, uočivši da je za dani niz kojemu
tražimo zbroj y0+y1+y2+...+yn
lako naći zbroj diferencija
di=yi-yi -1
uzastopnih članova niza:
d1+d2+...+dn=yn-y0.
Kad se, kao na slici gore desno, promatra površina ispod neke krivulje, možemo je aproksimirati
zbrojem njezinih ordinata yi u razmacima od po 1 jer su površine pravokutnika
jednake yi·1. Što je odabrana jedinica 1 manja,
to je zbroj tih površina
y1+y2+...+yn bliži
stvarnoj površini ispod krivulje. Budući da su razmaci između dva susjedna x-a jednaki
xi+1-xi=1,
slijedi da je koeficijent smjera sekante između dviju
susjednih (u smislu pomaka apscise za 1) točaka na grafu jednak
(yi+1-yi)/(xi+1-xi)=
yi+1-yi, tj. koeficijent smjera sekante je diferencija
niza y-a koji želimo zbrojiti. Također, što je odabrana jedinica 1 manja, to je koeficijent smjera
sekante bliži koeficijentu smjera tangente u lijevoj od dviju susjednih točaka.
Ako se odabrana jedinica 1 prozove dx, površina je jednaka zbroju izraza oblika ydx (za x
u određenim granicama), a koeficijent smjera tangente jednak je dy/dx, gdje je dy promjena
y ako se x promijeni za dx
(tj. dy je diferencija uzastopnih članova niza y-a).
Uočimo da je, za razliku od Newtona, von Leibniz
kao koeficijent smjera tangente dobio ne omjer fluksija, tj. brzina, nego omjer infinitezimalnih
prirasta osnovnih veličina (koje bi Newton zvao fluensi). S obzirom na vezu između zbrajanja niza i
njegova niza diferencija, von Leibniz zaključuje da inverznost tih operacija vrijedi i kad su razmaci
među članovima infinitezimalni, tj. zaključuje da su postupci integriranja i deriviranja međusobno inverzni,
dakle traženje koeficijenta smjera tangente i površine ispod krivulje međusobno su inverzni postupci.
Tako nakon par godina isprobavanja označavanja kako bi bilo što konzistentnije, von Leibniz dolazi do
i danas smislene notacije d∫dy=ydx.
Napomenimo
da su i ranije postojale metode integriranja tj. nalaženja površine (npr. starogrčka metoda ekshaustije)
te nalaženja tangente (npr. Descartesova i de Fermatova metoda), no razlog zašto se otkriće
infinitezimalnog računa pripisuje Newtonu i von Leibnizu jest njihovo otkriće osnovnog teorema
infinitezimalnog računa, tj. veze između tih dvaju postupaka.
Nakon von Leibnizova odgovora na Newtonovo drugo pismo, Newton je i dalje uvjeren da mu je von Leibniz ukrao metodu. Von Leibniz 1684. objavljuje Nova Methodus pro Maximis et Minimis, itemque Tangentibus... s detaljima svog diferencijalnog računa, a 1686. članak o integralnom računu. Kad je 1711. pročitao članak u Transactions of the Royal Society of London, u kojem je optužen za plagijat, von Leibniz traži ispriku, no autor članka Keill odbija je dati i argumentira da je von Leibniz iz Newtonovih pisama imao mogućnost ukrasti metodu. Von Leibniz se obraća Royal Society, koje postavlja komisiju za utvrđivanje prioriteta. Ta komisija nije od von Leibniza zatražila njegovu verziju, a izvještaj u korist Newtona napisao je sam Newton (1713.), u to doba predsjednik Royal Society. Von Leibniz 1714. objavljuje anonimni pamflet i kao argument u svoju korist poziva se na jednu Newtonovu grešku koju je uočio Johann Bernoulli (von Leibniz je imao intenzivne matematičke kontakte s braćom Bernoulli, koji su bitno utjecali na sređivanje von Leibnizovih rezultata). Keill objavljuje odgovor na taj pamflet, ponovno usmjeren protiv von Leibniza, a von Leibniz nakon toga odbija dalju raspravu s argumentom da ne može odgovarati idiotu. Na još jedno Newtonovo pismo von Leibniz je odgovorio detaljima svojih rezultata, no nije bilo Newtonove isprike ili kakvog drugog pokušaja mirenja. U povijesti se dugo smatralo da su argumenti na strani von Leibniza, pogotovo zbog poznatog nezgodnog Newtonovog karaktera. Ipak, ne možemo biti sigurni je li von Leibniz za svog boravka u Londonu vidio Newtonove rukopise i, inspiriran njima, izveo svoju varijantu infinitezimalnog računa. Sigurno je ipak da su obojica podjednako zaslužna za ovo otkriće, a da je von Leibniz potpuno drugačijim pristupom samostalno izveo svoje rezultate. Današnji oblik diferencijalnog i integralnog računa sličniji je von Leibnizovom jer je gotovo sve glavne današnje oznake i način pisanja (osim oznake ƒ′ za deriviranu funkciju koju je uveo Lagrange) uveo von Leibniz, a uz to je njegov pristup više matematički. Nasuprot njemu, Newtonov pristup više je fizikalan, a premda je imao svoje oznake, često ih je mijenjao i njegovi su tekstovi iz današnje perspektive nerazumljivi za čitanje.

Johann kontra Jacoba Bernoullija (i de L'Hôpitala)
ili: sukobi među braćom Braća Jacob (lijevo)
i Johann Bernoulli
bili su prva od tri generacije
obitelji Bernoulli,
koja je dala nekoliko velikih matematičara, među kojima je - uz spomenuta dva
brata - najpoznatiji Daniel Bernoulli, Johannov sin. Oba brata studirala
su druge predmete po želji oca, koji nije dopustio studij matematike.
Jacob Bernoulli (1654.-1705.) studirao
je teologiju i filozofiju, no već rano zanimala ga je matematika kojoj se posvetio
nakon završenog studija. Slično kao i on,
Johann Bernoulli (1667.-1748.) prvo
je studirao medicinu, a zatim se počeo baviti matematikom, koju je naučio uz
pomoć starijeg brata Jacoba. Oba su brata postala poznati i uspješni
matematičari. Jacob je osobito poznat po rezultatima iz teorije vjerojatnosti,
kojoj je upravo on dao moderni oblik. Johanna je više zanimala matematička analiza,
odnosno posljedice von Leibnizovog diferencijalnog i integralnog računa. Oba
su se pak brata bavila diferencijalnim jednadžbama i problemima varijacijskog
računa, koji predstavljaju početak danas vrlo razvijene discipline funkcionalne analize.
Tipičan problem varijacijskog računa je
problem brahistohrone, koji je postavio Johann Bernoulli 1696.:
Za dane
točke A i B u vertikalnoj ravnini treba odrediti krivulju po kojoj točka,
kojoj akceleraciju uzrokuje samo gravitacija, najbrže dolazi od A do B.
Tim se problemom ranije bavio Galileo i dobio krivo rješenje da
je ta krivulja luk kružnice. Johann je znao riješiti problem, ali ga je
1696. postavio kao izazov drugim matematičarima. Tako je dobiveno
pet rješenja - uz Johanna, problem su riješili i Jacob, te Newton,
von Leibniz i de l'Hôpital.
Braća Jacob (lijevo)
i Johann Bernoulli
bili su prva od tri generacije
obitelji Bernoulli,
koja je dala nekoliko velikih matematičara, među kojima je - uz spomenuta dva
brata - najpoznatiji Daniel Bernoulli, Johannov sin. Oba brata studirala
su druge predmete po želji oca, koji nije dopustio studij matematike.
Jacob Bernoulli (1654.-1705.) studirao
je teologiju i filozofiju, no već rano zanimala ga je matematika kojoj se posvetio
nakon završenog studija. Slično kao i on,
Johann Bernoulli (1667.-1748.) prvo
je studirao medicinu, a zatim se počeo baviti matematikom, koju je naučio uz
pomoć starijeg brata Jacoba. Oba su brata postala poznati i uspješni
matematičari. Jacob je osobito poznat po rezultatima iz teorije vjerojatnosti,
kojoj je upravo on dao moderni oblik. Johanna je više zanimala matematička analiza,
odnosno posljedice von Leibnizovog diferencijalnog i integralnog računa. Oba
su se pak brata bavila diferencijalnim jednadžbama i problemima varijacijskog
računa, koji predstavljaju početak danas vrlo razvijene discipline funkcionalne analize.
Tipičan problem varijacijskog računa je
problem brahistohrone, koji je postavio Johann Bernoulli 1696.:
Za dane
točke A i B u vertikalnoj ravnini treba odrediti krivulju po kojoj točka,
kojoj akceleraciju uzrokuje samo gravitacija, najbrže dolazi od A do B.
Tim se problemom ranije bavio Galileo i dobio krivo rješenje da
je ta krivulja luk kružnice. Johann je znao riješiti problem, ali ga je
1696. postavio kao izazov drugim matematičarima. Tako je dobiveno
pet rješenja - uz Johanna, problem su riješili i Jacob, te Newton,
von Leibniz i de l'Hôpital.
 Godine 1692. Johann u Parizu
susreće Guillaume François Antoine Marquis
de L'Hôpitala (1661.-1704., slika desno) i podučava ga Newton-Leibnizovom infinitezimalnom računu.
Na osnovi tih predavanja 1696. de l’Hôpital će objaviti prvi udžbenik
infinitezimalnog računa, ali bez spomena Johanna Bernoullija
(osim u zahvali u predgovoru). U toj se knjizi nalazi pravilo, danas poznato
kao l'Hôpitalovo, koje olakšava izračunavanje mnogih limesa. To je pravilo
zapravo otkrio Johann i dio je njegovih predavanja l'Hôpitalu. Ipak, l'Hôpital
nije bio loš matematičar koji je samo "ukrao" tuđe rezultate, već je u njegovoj
knjizi ispravljeno više grešaka Johanna Bernoullija.
Godine 1692. Johann u Parizu
susreće Guillaume François Antoine Marquis
de L'Hôpitala (1661.-1704., slika desno) i podučava ga Newton-Leibnizovom infinitezimalnom računu.
Na osnovi tih predavanja 1696. de l’Hôpital će objaviti prvi udžbenik
infinitezimalnog računa, ali bez spomena Johanna Bernoullija
(osim u zahvali u predgovoru). U toj se knjizi nalazi pravilo, danas poznato
kao l'Hôpitalovo, koje olakšava izračunavanje mnogih limesa. To je pravilo
zapravo otkrio Johann i dio je njegovih predavanja l'Hôpitalu. Ipak, l'Hôpital
nije bio loš matematičar koji je samo "ukrao" tuđe rezultate, već je u njegovoj
knjizi ispravljeno više grešaka Johanna Bernoullija.
 Godine 1691. Johann (slika lijevo)
je riješio problem koji je postavio Jacob o nalaženju formule krivulje
lančanice, tj. kosinusa hiperbolnog.
U to doba dva brata intenzivno surađuju i dobivaju
niz važnih rezultata, no uskoro će od suradnika postati rivali. U to doba Jacob
ima mjesto na sveučilištu u Baselu, a Johann ga ne može dobiti i mora tražiti drugo
namještenje. Johann se hvali svojim rezultatima, a Jacob ga grubo napada u tisku i
tvrdi kako ga je on svemu naučio. Kako su oba brata bila vrlo osjetljiva,
razdražljiva i željna priznanja, sukob se pojačava. Budući da
ne može dobiti mjesto u Baselu, Johann seli u Nizozemsku (otkud potječe
obitelj Bernoulli). Kad je Jacob 1697. riješio problem brahistohrone,
Johann je to pozdravio lijepim riječima, no došlo je do velike svađe u kojoj
je Jacob izazvao Johanna novim problemom sličnog tipa. Johann je riješio i taj
problem, a svađa se pojačava i iste godine Johann i Jacob potpuno prekidaju
komunikaciju. Johann se u Švicarsku vratio nakon Jacobove smrti i
naslijedio njegovo profesorsko mjesto na sveučilištu u Baselu.
Godine 1691. Johann (slika lijevo)
je riješio problem koji je postavio Jacob o nalaženju formule krivulje
lančanice, tj. kosinusa hiperbolnog.
U to doba dva brata intenzivno surađuju i dobivaju
niz važnih rezultata, no uskoro će od suradnika postati rivali. U to doba Jacob
ima mjesto na sveučilištu u Baselu, a Johann ga ne može dobiti i mora tražiti drugo
namještenje. Johann se hvali svojim rezultatima, a Jacob ga grubo napada u tisku i
tvrdi kako ga je on svemu naučio. Kako su oba brata bila vrlo osjetljiva,
razdražljiva i željna priznanja, sukob se pojačava. Budući da
ne može dobiti mjesto u Baselu, Johann seli u Nizozemsku (otkud potječe
obitelj Bernoulli). Kad je Jacob 1697. riješio problem brahistohrone,
Johann je to pozdravio lijepim riječima, no došlo je do velike svađe u kojoj
je Jacob izazvao Johanna novim problemom sličnog tipa. Johann je riješio i taj
problem, a svađa se pojačava i iste godine Johann i Jacob potpuno prekidaju
komunikaciju. Johann se u Švicarsku vratio nakon Jacobove smrti i
naslijedio njegovo profesorsko mjesto na sveučilištu u Baselu.

Gauss kontra Legendrea
ili: svađe oko brojeva i aproksimacija Johann
Carl Friedrich Gauss (1777.-1855.) sigurno je jedan od najpoznatijih i najvećih
matematičara svih vremena. Od anegdota kako je kao dijete brzo zbrojio brojeve od 1 do 100
pa do velikih teorema, poput
osnovnog teorema aritmetike (svaki prirodan broj
može se na jedinstven način - do na poredak - faktorizirati na proste faktore)
i osnovnog teorema algebre
(polinom s kompleksnim koeficijentima stupnja n ima n kompleksnih nultočaka),
koje je prvi dokazao, Gauss je pojam
svakome tko išta zna o matematici. Jedan od njegovih glavnih interesa bila je
teorija brojeva, u kojoj je dokazao niz važnih rezultata. Nešto manje poznati
matematičar bio je također velikan teorije brojeva,
Adrien
Marie Legendre (1752.-1833.). Legendre i Gauss sukobit će se oko
prvenstva za tri važna matematička rezultata, dva iz teorije brojeva, a treći
iz teorije aproksimacija. Preciznije, radilo se o zakonu kvadratnog reciprociteta,
gustoći prostih brojeva i metodi najmanjih kvadrata.
Johann
Carl Friedrich Gauss (1777.-1855.) sigurno je jedan od najpoznatijih i najvećih
matematičara svih vremena. Od anegdota kako je kao dijete brzo zbrojio brojeve od 1 do 100
pa do velikih teorema, poput
osnovnog teorema aritmetike (svaki prirodan broj
može se na jedinstven način - do na poredak - faktorizirati na proste faktore)
i osnovnog teorema algebre
(polinom s kompleksnim koeficijentima stupnja n ima n kompleksnih nultočaka),
koje je prvi dokazao, Gauss je pojam
svakome tko išta zna o matematici. Jedan od njegovih glavnih interesa bila je
teorija brojeva, u kojoj je dokazao niz važnih rezultata. Nešto manje poznati
matematičar bio je također velikan teorije brojeva,
Adrien
Marie Legendre (1752.-1833.). Legendre i Gauss sukobit će se oko
prvenstva za tri važna matematička rezultata, dva iz teorije brojeva, a treći
iz teorije aproksimacija. Preciznije, radilo se o zakonu kvadratnog reciprociteta,
gustoći prostih brojeva i metodi najmanjih kvadrata.
 Legendre je 1785. prvi dao
dokaz zakona kvadratnog reciprociteta, no dokaz nije bio potpuno točan. Taj je
zakon prvi izrekao
Euler
i u to je doba to najpoznatiji otvoreni problem teorije brojeva. Radi se o paralelnom
rješavanju dviju kvadratnih kongruencija. Podsjetimo se da je kongruencija izraz
oblika a≡b(mod n), koji znači da n dijeli a-b,
npr. 50≡2 (mod 6) jer je 50-2=48 djeljivo sa 6. Kongruencija zapravo kaže
da a i b imaju isti ostatak pri dijeljenju s n. S obzirom da ako
n dijeli a-b, onda dijeli i b-a, svejedno je pišemo li
a≡b (mod n) ili b≡a(mod n).
Zakon kvadratnog reciprociteta kaže da su kvadratne kongruencije
x2≡p(mod q) i x2≡q
(mod p) ili obje rješive ili obje nerješive
za sve proste brojeve p i q, osim
ako oba pri dijeljenju s 4 daju ostatak 3 (i u tom je slučaju rješiva točno
jedna od tih dviju kongruencija). Drugim riječima, ako je ostatak pri dijeljenju
p s q moguće zapisati kao kvadratni broj, onda je i ostatak
pri dijeljenju q s p kvadratni broj, osim ako i p i q
imaju ostatak 3 pri dijeljenju s 4. Pritom pod "ostatak" podrazumijevamo bilo koji
oblik ostataka do na višekratnik djelitelja (npr. pri dijeljenju 11 s 5 ostatak
1 možemo zapisati i kao 1 plus ili minus bilo koji višekratnik od 5 jer
se time ne mijenja definicija ostatka pri dijeljenju a:b kao broja r
sa svojstvom da je a-r djeljivo s b).
Svoj prvi dokaz zakona kvadratnog reciprociteta Legendre je donekle popravio 1798.,
no dokaz još nije bio potpun. Gauss je zakon potpuno točno dokazao 1801. godine
te je tada kritizirao ranije Legendreove pokušaje i istaknuo svoje prvenstvo.
Legendre je 1785. prvi dao
dokaz zakona kvadratnog reciprociteta, no dokaz nije bio potpuno točan. Taj je
zakon prvi izrekao
Euler
i u to je doba to najpoznatiji otvoreni problem teorije brojeva. Radi se o paralelnom
rješavanju dviju kvadratnih kongruencija. Podsjetimo se da je kongruencija izraz
oblika a≡b(mod n), koji znači da n dijeli a-b,
npr. 50≡2 (mod 6) jer je 50-2=48 djeljivo sa 6. Kongruencija zapravo kaže
da a i b imaju isti ostatak pri dijeljenju s n. S obzirom da ako
n dijeli a-b, onda dijeli i b-a, svejedno je pišemo li
a≡b (mod n) ili b≡a(mod n).
Zakon kvadratnog reciprociteta kaže da su kvadratne kongruencije
x2≡p(mod q) i x2≡q
(mod p) ili obje rješive ili obje nerješive
za sve proste brojeve p i q, osim
ako oba pri dijeljenju s 4 daju ostatak 3 (i u tom je slučaju rješiva točno
jedna od tih dviju kongruencija). Drugim riječima, ako je ostatak pri dijeljenju
p s q moguće zapisati kao kvadratni broj, onda je i ostatak
pri dijeljenju q s p kvadratni broj, osim ako i p i q
imaju ostatak 3 pri dijeljenju s 4. Pritom pod "ostatak" podrazumijevamo bilo koji
oblik ostataka do na višekratnik djelitelja (npr. pri dijeljenju 11 s 5 ostatak
1 možemo zapisati i kao 1 plus ili minus bilo koji višekratnik od 5 jer
se time ne mijenja definicija ostatka pri dijeljenju a:b kao broja r
sa svojstvom da je a-r djeljivo s b).
Svoj prvi dokaz zakona kvadratnog reciprociteta Legendre je donekle popravio 1798.,
no dokaz još nije bio potpun. Gauss je zakon potpuno točno dokazao 1801. godine
te je tada kritizirao ranije Legendreove pokušaje i istaknuo svoje prvenstvo.
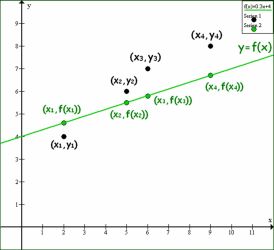 U isto doba, oko 1800. godine, Legendre se bavi
metodom najmanjih kvadrata koja daje način kako
sa što manjom greškom izračunati koeficijente nepoznate (npr. linearne) funkcije
koja procjenjuje neke podatke mjerenja. Na slici lijevo zeleno je nacrtan
pravac koji se dobije metodom najmanjih kvadrata ako su kao rezultati mjerenja
veličine y u pozicijama x dobivene crne točke.
Ideja, dakle, nije provući krivulju
točno kroz te poznate točke - na kraju krajeva, možda u njima postoji i neka
greška mjerenja - nego naći krivulju
koja od njih što manje odstupa, a daje
dobru procjenu za ostale x-eve. Potreba za takvom metodom pojavila se u
astronomiji, u kojoj je često bilo dostupno samo nekoliko mjerenja položaja
nebeskog tijela, a željelo se procijeniti njegov položaj u nekom trenutku u
kojem ga se ne vidi ili ne mjeri. Legendre je metodu najmanjih kvadrata, koja je i danas
jedna od najvažnijih ako ne i najvažnija metoda za procjene podataka, izveo
do 1806. U isto vrijeme i neovisno o njemu, Gauss ju je također razvio radi
procjene putanje nedavno otkrivenog planetoida Ceresa. Objavio ju je tek 1809.
i tom prilikom izjavio da ju je on otkrio prije Legendrea. Godine 1808.
Legendre je dao novi dokaz zakona kvadratnog reciprociteta i pritom korektno
citirao Gaussa. U istom djelu u kojem je objavio taj dokaz dao je i procjenu broja
prostih brojeva manjih od n (tzv.
gustoća prostih brojeva π(n)).
I za tu procjenu, koju će Gauss nezavisno od njega dobiti u malo drugačijem obliku
Gauss će tvrditi da ju je prvi otkrio. Tada više ne sasvim
mladi, a ugledni matematičar Legendre, jako je povrijeđen ovim kritikama i izjavljuje:
Ovakva drskost neshvatljiva je za čovjeka koji ima dovoljno osobnih zasluga
da nema potrebe prisvajati tuđa otkrića.
U isto doba, oko 1800. godine, Legendre se bavi
metodom najmanjih kvadrata koja daje način kako
sa što manjom greškom izračunati koeficijente nepoznate (npr. linearne) funkcije
koja procjenjuje neke podatke mjerenja. Na slici lijevo zeleno je nacrtan
pravac koji se dobije metodom najmanjih kvadrata ako su kao rezultati mjerenja
veličine y u pozicijama x dobivene crne točke.
Ideja, dakle, nije provući krivulju
točno kroz te poznate točke - na kraju krajeva, možda u njima postoji i neka
greška mjerenja - nego naći krivulju
koja od njih što manje odstupa, a daje
dobru procjenu za ostale x-eve. Potreba za takvom metodom pojavila se u
astronomiji, u kojoj je često bilo dostupno samo nekoliko mjerenja položaja
nebeskog tijela, a željelo se procijeniti njegov položaj u nekom trenutku u
kojem ga se ne vidi ili ne mjeri. Legendre je metodu najmanjih kvadrata, koja je i danas
jedna od najvažnijih ako ne i najvažnija metoda za procjene podataka, izveo
do 1806. U isto vrijeme i neovisno o njemu, Gauss ju je također razvio radi
procjene putanje nedavno otkrivenog planetoida Ceresa. Objavio ju je tek 1809.
i tom prilikom izjavio da ju je on otkrio prije Legendrea. Godine 1808.
Legendre je dao novi dokaz zakona kvadratnog reciprociteta i pritom korektno
citirao Gaussa. U istom djelu u kojem je objavio taj dokaz dao je i procjenu broja
prostih brojeva manjih od n (tzv.
gustoća prostih brojeva π(n)).
I za tu procjenu, koju će Gauss nezavisno od njega dobiti u malo drugačijem obliku
Gauss će tvrditi da ju je prvi otkrio. Tada više ne sasvim
mladi, a ugledni matematičar Legendre, jako je povrijeđen ovim kritikama i izjavljuje:
Ovakva drskost neshvatljiva je za čovjeka koji ima dovoljno osobnih zasluga
da nema potrebe prisvajati tuđa otkrića.
| Za kraj ovog sukoba koji je ostao otvoren - nije diskutabilno da su Gaussovi dokazi precizniji i potpuniji, ali ni da je Legendre imao samostalne i bitne doprinose - recimo nekoliko riječi o temi spomenutog trećeg sukoba oko prioriteta, tj. Gaussovoj i Legendreovoj procjeni gustoće prostih brojeva. Legendre je dobio rezultat da je π(n) približno jednak n podijeljenom s ln n - 1,08366... (broj 1,08366 dobiven je empirijski i zove se Legendreova konstanta), a Gauss je dobio procjenu π(n) kao određenog integrala od 2 do n recipročne vrijednosti prirodnog logaritma. Kad se usporede vrijednosti, dobije se tablica desno (stupac π(n) daje točnu vrijednost). Vidimo da je Gaussova procjena nešto bolja kod velikih n, dok je Legendreova nešto bolja kod manjih, no obje daju točan red veličine za π(n). |

Cauchy kontra mnogih (ili obrnuto :-)
ili: kako nestaju matematički radovi?  Po Augustinu Louisu Cauchyju (1789.-1857.)
danas se zove niz osnovnih pojmova matematičke analize: Cauchyjev niz, Cauchy-Riemannovi
uvjeti, Cauchyjev integralni teorem ... Prvi je precizirao uvjete konvergencije redova,
precizno definirao neprekidnost i integral i dr. Iznimno produktivan matematičar, napisao je čak
789 matematičkih radova, sistematizirao i precizirao matematičku analizu i utemeljio kompleksnu
analizu (analizu kompleksnih funkcija kompleksne varijable). U njegovu djetinjstvu
Lagrange i Laplace bili su gosti obitelji. Prve matematičke rezultate objavio je 1812.,
a slavu je stekao dokazom jedne Fermatove hipoteze o poligonalnim brojevima (1816.). Bavio se i
nekim područjima fizike i u njima dobio važne rezultate. Bio je poznat kao nezgodan i arogantan, sklon potcjenjivanju
tuđih rezultata, imao je loš odnos s drugim znanstvenicima. Iako je dobio niz vlastitih
rezultata, često je koristio i tuđe, uz eventualne prepravke,
i prisvajao ih bez navođenja stvarnog autora.
Po Augustinu Louisu Cauchyju (1789.-1857.)
danas se zove niz osnovnih pojmova matematičke analize: Cauchyjev niz, Cauchy-Riemannovi
uvjeti, Cauchyjev integralni teorem ... Prvi je precizirao uvjete konvergencije redova,
precizno definirao neprekidnost i integral i dr. Iznimno produktivan matematičar, napisao je čak
789 matematičkih radova, sistematizirao i precizirao matematičku analizu i utemeljio kompleksnu
analizu (analizu kompleksnih funkcija kompleksne varijable). U njegovu djetinjstvu
Lagrange i Laplace bili su gosti obitelji. Prve matematičke rezultate objavio je 1812.,
a slavu je stekao dokazom jedne Fermatove hipoteze o poligonalnim brojevima (1816.). Bavio se i
nekim područjima fizike i u njima dobio važne rezultate. Bio je poznat kao nezgodan i arogantan, sklon potcjenjivanju
tuđih rezultata, imao je loš odnos s drugim znanstvenicima. Iako je dobio niz vlastitih
rezultata, često je koristio i tuđe, uz eventualne prepravke,
i prisvajao ih bez navođenja stvarnog autora.
Od 1815. predavao je na znamenitoj École Polytechnique, a 1816. postaje i članom Francuske akademije znanosti. Nakon srpanjske revolucije 1830., kao zagovornik starog režima, odlazi u Švicarsku, a novi režim od Cauchyja zahtijeva zakletvu o podršci, što Cauchy odbija i gubi sve pozicije u Parizu. 1831. odlazi u Torino, 1833. u Prag, a 1838. vratio se u Pariz na poziciju u Akademiji, no zbog političkih i vjerskih uvjerenja (ekstremni katolik) ne dobiva pravo držati nastavu. Kad je Louis Philippe svrgnut 1848., Cauchy vraća svoje pozicije na sveučilištu. Tijekom cijele karijere stvarao je probleme kolegama (npr. 1850. za College de France izabran je Liouville, a Cauchy je pokušao izmijeniti tu odluku). Potkraj života sukobio se s Duhamelom oko prvenstva u jednom rezultatu o neelastičnim sudarima i, iako se dokazalo da je u krivu, Cauchy je to odbio priznati. Među matematičarima čije je radove zagubio, ignorirao ili prisvojio bilo je nekoliko velikih imena: Abel, Galois, Grassmann, Saint-Venant, Argand.
 Norveški matematičar
Niels Henrik Abel (1802.-1829.) cijeli je kratki život proveo u siromaštvu, a njegovi su
iznimni rezultati postali slavni tek nakon njegove smrti. Za boravka u Parizu pokušavao
je prezentirati svoj rad o eliptičkim integralima i funkcijama, koji je danas priznat kao izniman i temeljni
rad za to područje. Prema Abelovim riječima, kad ga je pokazao Cauchyju, on se jedva udostojao
baciti pogled na njega, a izjavio je i: Cauchy je lud i tu se ne može ništa napraviti
iako je trenutno on jedini koji zna kako treba raditi matematiku.
Kao recenzenti rada imenovani su Cauchy i Legendre, a Abel je
čekao njihov izvještaj u Parizu i gotovo izgladnio zbog nedostatka novca. Kad više nije mogao
izdržati boravak u Parizu, vratio se u Norvešku i tamo saznao da je njegov pariški rad zagubljen.
Ubrzo zatim umro je od tuberkuloze, točno u trenutku kad mu je konačno osigurano mjesto na
sveučilištu u Berlinu. Nakon njegove smrti, Cauchy je 1830. nakon mnogo traženja
našao zagubljeni rad i dao vrlo površan izvještaj, a rad je tiskan 1841.
(i tada je ponovno nestao i ponovno je nađen tek 1952.).
Godine 1830. Francuska akademija znanosti je
dodijelila svoj Grand Prix Jacobiju
i posthumno Abelu za njihove
radove o eliptičkim integralima i eliptičkim funkcijama.
Norveški matematičar
Niels Henrik Abel (1802.-1829.) cijeli je kratki život proveo u siromaštvu, a njegovi su
iznimni rezultati postali slavni tek nakon njegove smrti. Za boravka u Parizu pokušavao
je prezentirati svoj rad o eliptičkim integralima i funkcijama, koji je danas priznat kao izniman i temeljni
rad za to područje. Prema Abelovim riječima, kad ga je pokazao Cauchyju, on se jedva udostojao
baciti pogled na njega, a izjavio je i: Cauchy je lud i tu se ne može ništa napraviti
iako je trenutno on jedini koji zna kako treba raditi matematiku.
Kao recenzenti rada imenovani su Cauchy i Legendre, a Abel je
čekao njihov izvještaj u Parizu i gotovo izgladnio zbog nedostatka novca. Kad više nije mogao
izdržati boravak u Parizu, vratio se u Norvešku i tamo saznao da je njegov pariški rad zagubljen.
Ubrzo zatim umro je od tuberkuloze, točno u trenutku kad mu je konačno osigurano mjesto na
sveučilištu u Berlinu. Nakon njegove smrti, Cauchy je 1830. nakon mnogo traženja
našao zagubljeni rad i dao vrlo površan izvještaj, a rad je tiskan 1841.
(i tada je ponovno nestao i ponovno je nađen tek 1952.).
Godine 1830. Francuska akademija znanosti je
dodijelila svoj Grand Prix Jacobiju
i posthumno Abelu za njihove
radove o eliptičkim integralima i eliptičkim funkcijama.
 Kao i Abel,
Evariste Galois (1811.-1832.)
umro je mlad i nepoznat, usprkos iznimnim rezultatima. Zajednički s
Abelom bio mu je i interes za pitanje rješivosti jednadžbi stupnja 5 i višeg u radikalima. Jednadžba
je rješiva u radikalima ako se njezina rješenja (kao u slučajima jednadžbi stupnja 1,2,3,4)
mogu izraziti preko koeficijenata jednadžbe pomoću konačno mnogo operacija zbrajanja, oduzimanja,
množenja, dijeljenja i korjenovanja. Za razliku od Abela, koji je dokazao da se
opća jednadžba stupnja
5 ne može riješiti u radikalima, Galois je dao opći postupak kojim se
za svaku jednadžbu bilo kojeg
stupnja može provjeriti imaju li takvo rješenje. Metoda koju je dobio postala je temelj danas vrlo razvijene
i široko primijenjene discipline
teorije grupa.
Pojednostavljeno rečeno, grupa je svaki skup s na njemu definiranom operacijom (npr. skup cijelih
brojeva sa zbrajanjem) koja daje rezultat
u tom istom skupu (zbroj dvaju cijelih brojeva je cijeli broj), asocijativna je
(tj. možemo pomicati
zagrade: (m+n)+k=m+(n+k),
ima neutralni element (element skupa takav da operacija s njim ništa ne mijenja,
npr. u Z s operacijom + to je 0 jer 0+n=n+0=n) i svaki element ima inverzan (element takav
da operacija s njime daje neutralni element, npr. u Z za svaki n je njegov inverzni element
-n jer je
n+(-n)=(-n)+n=0). Drugačije rečeno,
grupa je skup s operacijom koja, ako je označena kao množenje, dopušta rješavanje
linearnih jednadžbi u tom skupu. Grupe se pojavljuju kako u čistoj matematici, tako i u primjenama
(npr. u kristalografiji) ili čak i u zabavi (npr. Rubikova kocka). Godine 1829. Galois je predao članak o rješenju algebarskih
jednadžbi Akademiji znanosti, a kao
recenzent imenovan je Cauchy, koji je zagubio rad. Kasnije je poslao i druge članke Cauchyju i
Fourieru, no i oni su zagubljeni. Na Cauchyjev nagovor čak je povukao jedan članak i
umjesto njega predao drugi za Grand Prix Akademije
(upravo onaj koji će dobiti Abel), no u to je doba već uvjeren da je
sustav u Francuskoj takav da onemogućava napredovanje kreativnim pojedincima. Galois je bio
revolucionarno nastrojen i cijeli mu je život obilježen političkim aktivnostima
zbog kojih je završavao i u zatvoru. Kad je tako zbog nošenja zabranjene uniforme Nacionalne
garde i oružja uhapšen i osuđen na zatvor 1831., u njemu je upoznao kćer zatvorskog
doktora i zaljubio se,
no kad je pušten 1832., ona više nije htjela čuti za njega. Pod sumnjivim i vrlo vjerojatno
politički obojenim okolnostima, a formalno radi zaštite njezine časti, izazvan je na dvoboj u
kojem je i poginuo. Noć prije dvoboja, znajući da nema šansu preživjeti, zapisao je sve svoje
glavne rezultate. Njih će tek 1846. objaviti Liouville. Zanimljivo je da je 1845. Cauchy dao
definiciju grupe koja je potpuno analogna Galoisovom koceptu, iako Galois nikad nije eksplicitno
dao definiciju grupe.
Kao i Abel,
Evariste Galois (1811.-1832.)
umro je mlad i nepoznat, usprkos iznimnim rezultatima. Zajednički s
Abelom bio mu je i interes za pitanje rješivosti jednadžbi stupnja 5 i višeg u radikalima. Jednadžba
je rješiva u radikalima ako se njezina rješenja (kao u slučajima jednadžbi stupnja 1,2,3,4)
mogu izraziti preko koeficijenata jednadžbe pomoću konačno mnogo operacija zbrajanja, oduzimanja,
množenja, dijeljenja i korjenovanja. Za razliku od Abela, koji je dokazao da se
opća jednadžba stupnja
5 ne može riješiti u radikalima, Galois je dao opći postupak kojim se
za svaku jednadžbu bilo kojeg
stupnja može provjeriti imaju li takvo rješenje. Metoda koju je dobio postala je temelj danas vrlo razvijene
i široko primijenjene discipline
teorije grupa.
Pojednostavljeno rečeno, grupa je svaki skup s na njemu definiranom operacijom (npr. skup cijelih
brojeva sa zbrajanjem) koja daje rezultat
u tom istom skupu (zbroj dvaju cijelih brojeva je cijeli broj), asocijativna je
(tj. možemo pomicati
zagrade: (m+n)+k=m+(n+k),
ima neutralni element (element skupa takav da operacija s njim ništa ne mijenja,
npr. u Z s operacijom + to je 0 jer 0+n=n+0=n) i svaki element ima inverzan (element takav
da operacija s njime daje neutralni element, npr. u Z za svaki n je njegov inverzni element
-n jer je
n+(-n)=(-n)+n=0). Drugačije rečeno,
grupa je skup s operacijom koja, ako je označena kao množenje, dopušta rješavanje
linearnih jednadžbi u tom skupu. Grupe se pojavljuju kako u čistoj matematici, tako i u primjenama
(npr. u kristalografiji) ili čak i u zabavi (npr. Rubikova kocka). Godine 1829. Galois je predao članak o rješenju algebarskih
jednadžbi Akademiji znanosti, a kao
recenzent imenovan je Cauchy, koji je zagubio rad. Kasnije je poslao i druge članke Cauchyju i
Fourieru, no i oni su zagubljeni. Na Cauchyjev nagovor čak je povukao jedan članak i
umjesto njega predao drugi za Grand Prix Akademije
(upravo onaj koji će dobiti Abel), no u to je doba već uvjeren da je
sustav u Francuskoj takav da onemogućava napredovanje kreativnim pojedincima. Galois je bio
revolucionarno nastrojen i cijeli mu je život obilježen političkim aktivnostima
zbog kojih je završavao i u zatvoru. Kad je tako zbog nošenja zabranjene uniforme Nacionalne
garde i oružja uhapšen i osuđen na zatvor 1831., u njemu je upoznao kćer zatvorskog
doktora i zaljubio se,
no kad je pušten 1832., ona više nije htjela čuti za njega. Pod sumnjivim i vrlo vjerojatno
politički obojenim okolnostima, a formalno radi zaštite njezine časti, izazvan je na dvoboj u
kojem je i poginuo. Noć prije dvoboja, znajući da nema šansu preživjeti, zapisao je sve svoje
glavne rezultate. Njih će tek 1846. objaviti Liouville. Zanimljivo je da je 1845. Cauchy dao
definiciju grupe koja je potpuno analogna Galoisovom koceptu, iako Galois nikad nije eksplicitno
dao definiciju grupe.
Jean Robert Argand u povijesti matematike ostao je zapamćen po Argandovom dijagramu, tj. prikazu kompleksnih brojeva u ravnini: os apscisa koristi se za prikaz realnog dijela, a ordinata za prikaz imaginarnog dijela, pa kompleksnom broju odgovara točka kojoj su koordinate njegov realni i imaginarni dio. Tako imaginarnoj jedinici i odgovara 1 na osi ordinata. Kako je horizontalna os realna, možemo reći i da imaginarnoj jedinici odgovara rotacija realne jedinice za pravi kut (u pozitivnom smjeru). Na taj način kompleksni brojevi mogu se interpretirati i kao rotacije ravnine. Tu je ideju Argand razvio 1814. Argand je u dva navrata (1806. i 1814.) dao i (ne baš potpune) dokaze osnovnog teorema algebre (polinom s kompleksnim koeficijentima stupnja n ima n kompleksnih nultočaka). Godine 1820. Cauchy u svojoj Cours d'analyse posvećuje čitavo poglavlje Argandovom dokazu, a da ga nije ni spomenuo! Napomenimo samo da je potpun dokaz osnovnog teorema algebre dao Gauss (1816.).
 Jedan od utemeljitelja moderne
linearne algebre bio je
Hermann Grassmann (1809.-1877.).
Godine 1844. Grassmann je dao apstraktnu definiciju algebre (skup u kojem možemo
zbrajati elemente, množiti ih realnim - ili kompleksnim - brojevima te množiti ih međusobno,
uz odgovarajuću usklađenost tih operacija; primjer je standardni vektorski prostor V
Jedan od utemeljitelja moderne
linearne algebre bio je
Hermann Grassmann (1809.-1877.).
Godine 1844. Grassmann je dao apstraktnu definiciju algebre (skup u kojem možemo
zbrajati elemente, množiti ih realnim - ili kompleksnim - brojevima te množiti ih međusobno,
uz odgovarajuću usklađenost tih operacija; primjer je standardni vektorski prostor V

Kronecker kontra Cantora
ili: postoji li ono što ne znamo konstruirati?
 Članak ćemo završiti sukobom koji
je poput prvog opisanog više filozofske, a manje matematičke
naravi. Georg Cantor (1845.-1918., slika lijevo) ušao je u povijest
kao tvorac teorije skupova na temelju koje
se razvila čitava matematika dvadesetog stoljeća, a
Leopold Kronecker (1823.-1891., slika desno)
ostao je poznat samo po Kroneckerovom δ-simbolu te po tome što je zbog njega Cantor
završio u ludnici...
Članak ćemo završiti sukobom koji
je poput prvog opisanog više filozofske, a manje matematičke
naravi. Georg Cantor (1845.-1918., slika lijevo) ušao je u povijest
kao tvorac teorije skupova na temelju koje
se razvila čitava matematika dvadesetog stoljeća, a
Leopold Kronecker (1823.-1891., slika desno)
ostao je poznat samo po Kroneckerovom δ-simbolu te po tome što je zbog njega Cantor
završio u ludnici...
Ipak, nije baš točno reći da je Cantor u ludnici završio zbog Kroneckera, iako je njihov sukob utjecao na razvoj Cantorovih depresija koje su kulminirale ekscentričnim ponašanjem krajem njegove karijere, kad je na matematičkim konferencijama izlagao teoriju da je Roger Bacon napisao Shakespearove drame.
Sve je počelo Cantorovim pokušajima da precizno opiše skup realnih brojeva. U tu svrhu počeo je promatrati beskonačne skupove i provjeravati njihova svojstva. Prvo je pokazao da skup cijelih brojeva ima jednako elemenata kao i skup prirodnih brojeva. Zatim je pokazao i da skup racionalnih brojeva ima isto toliko elemenata, pa onda i da skup svih algebarskih brojeva također ima jednako mnogo elemenata kao skup prirodnih brojeva. Danas skupove koji imaju jednako mnogo elemenata kao skup prirodnih brojeva zovemo prebrojivi skupovi. Za dva skupa definiramo da imaju jednako mnogo elemenata ako između njih možemo uspostaviti bijekciju, tj. funkciju takvu da svaki element kodomene ima jedinstveni original u domeni (koji se putem te funkcije preslika u njega). U slučaju konačnih skupova ta se definicija podudara s intuitivnim shvaćanjem jednakosti broja elemenata skupova.
Postavilo se prirodno pitanje ima li i realnih brojeva jednako mnogo kao prirodnih tj. je
li skup R prebrojiv? Cantor uspijeva pokazati da to nije točno i
taj trenutak (1873.) smatra se
nastankom teorije skupova koja je omogućila razlikovanje beskonačnih skupova po broju elemenata.
Svoj prvi dokaz poboljšao je već 1874. i time uveo znameniti
Cantorov dijagonalni postupak, a
njegovim varijacijama pokazani su i mnogi drugi teoremi o brojevima elemenata skupova.
Ideja ovog dokaza slijedi. Pretpostavimo da je R prebrojiv. To znači da je
i otvoreni interval <0,1> prebrojiv, a to pak znači
da sve brojeve iz <0,1> možemo poredati u niz
x1, x2, x3,
x4, ... Pretpostavimo
da su oni zapisani u decimalnom sustavu, npr.
x1=0 , 5 1 0 5 1 1 0 ...
x2=0 , 4 1 3 2 0 4 3 ...
x3=0 , 8 2 4 5 0 2 6 ...
x4=0 , 2 3 3 0 1 2 6 ...
itd.
Sad pogledamo za x1 njegovu prvu znamenku iza decimalnog zareza (5),
za x2 drugu (1), za x3 treću (4) itd.
Formiramo novi broj x
iz intervala <0,1> tako da mu za prvu znamenku iza decimalnog zareza uzmemo 1,
za drugu 2, za treću 1 itd. po pravilu: i-ta znamenka po redu je 1 osim
ako je i-ta znamenka od xi bila 1 i u tom slučaju
stavimo znamenku 2. Ideja je da očitamo broj kojem su decimalne znamenke iza nule redom
dijagonalne znamenke (gore označene podebljano) i onda je x neki broj koji nema s
tom dijagonalom redom nijednu istu decimalnu znamenku. Tada se taj x razlikuje od
svih brojeva u gornjem nizu (od svakog barem na njegovom dijagonalnom mjestu), a to je
nemoguće jer smo pretpostavili da su u nizu ispisani svi brojevi iz intervala.
Zaključujemo da interval ne možemo zapisati kao niz, tj. skup R nije prebrojiv. Iz ovog se
teorema kao jednostavna posljedica dobiva da postoji beskonačno mnogo transcendentnih brojeva,
što je bilo iznimno zapanjujuće jer su tek nedavno nađeni prvi konkretni
transcendentni brojevi (Liouville je 1844. dosta komplicirano konstruirao
njih beskonačno mnogo, a Hermite je - također ne baš jednostavno - 1873.
dokazao da je
e=2.718281828459045235...
transcendentan).
Kad je Cantor pokušao objaviti svoje rezultate u uglednom časopisu Crelle's Journal, u kojem je jedan od urednika bio Kronecker, naišao je na jak otpor. Kronecker je bio na čelu tada utjecajne struje konstruktivista, matematičara koji su priznavali samo one matematičke dokaze o postojanju objekata ako su ti dokazi davali i metodu konstrukcije tih objekata. Cantorovi su pak dokazi očigledno nekonstruktivistički. Članak je objavljen tek kad je u Cantorovu korist intervenirao njegov prijatelj, matematičar Richard Dedekind. Kako u to doba Cantor pokazuje prve znakove depresije, dugo se smatralo da ona potječe od tih problema s objavom rezultata, no na osnovi modernih spoznaja o bolesti depresije možemo reći da su ovi problemi bili povod, ali ne i uzrok bolesti. Do ponovnog sukoba dolazi kad 1878. Cantor opet u Crelle's Journalu želi objaviti rezultat da dužina ima jednako mnogo elemenata kao i kvadrat. Ovaj, čak i za samog Cantora, šokantan rezultat (sam je nakon dokaza komentirao: "Vidim, ali ne vjerujem!") otvorio je pitanje razlikovanja dimenzija, koje je tek tridesetak godina kasnije precizno razjašnjeno. Za ovaj dokaz potrebno je uspostaviti bijekciju intervala s uređenim parovima elemenata tog intervala, a nju Cantor definira tako da broju x pridružuje par (y,z) tako da znamenke od x razbija na blokove: svaka nula ili niz nula ide u isti blok s prvom nenul znamenkom iza tih nula, a ostale nenul znamenke svaka su svoj blok. Npr. x=0 , |5 | 1 | 05 | 1 | 2 | 001 |... razbijen je na blokove okomitim crtama. Sad se y formira iz prvog, trećeg, itd. svih neparnih blokova, tj. y=0,5052..., a z iz parnih blokova, tj. z=0,11001...
Nakon bolovanja 1884. Cantor se htio pomiriti s Kroneckerom i on je to prihvatio, ali filozofske razlike ostaju. Kad je 1891. održan prvi sastanak Njemačkog matematičkog društva (Deutsche Mathematikervereinigung), kojem je Cantor suosnivač, on poziva Kroneckera na taj sastanak. No, Kronecker nije mogao doći zbog ženine smrti, a i sam uskoro umire. Cantor je umro u sanatoriju, od posljedica srčanog udara, no zadnjih dvadesetak godina života većim je dijelom proveo u sanatorijima s povremenim periodima rada.

Popis literature i linkova
[1] W. S. Anglin, J. Lambek, The Heritage of Thales, Springer Verlag 1995.
[2] W. W. Rouse Ball, A Short Account of the History of Mathematics, Dover 1960.
[3] Mac Tutor History Archives, http://www-groups.dcs.st-and.ac.uk/~history
[4] R. Mankiewicz, THE STORY OF MATHEMATICS From counting to complexity, Orion Publishing Co. 2000.
[4] Z. Šikić, Kako je stvarana novovjekovna matematika, Školska knjiga 1989.

Uvod
Hipasus kontra Pitagore
Tartaglia kontra Cardana
Viète kontra van Roomena
Descartes kontra de Fermata
Newton kontra von Leibniza
Johann kontra Jacoba Bernoullija (i de l'Hôpitala)
Gauss kontra Legendrea
Cauchy kontra mnogih
Kronecker kontra Cantora
Popis literature i linkova