
Broj 7

































Hrvoje Čavrak
Catalanovi brojevi


Sadržaj:
1. Uvod
2. Problemi vezani uz Catalanove brojeve
2.1 Triangulacija konveksnog n-terokuta
2.2 Redoslijed množenja
2.3 Problem zagrađivanja
2.4 Putovi u cjelobrojnoj mreži
2.5 Dyckovi planinski putovi
2.6 Problem rukovanja
2.7 Problem binarnih stabala
3. Funkcija izvodnica za Catalanove brojeve
4. Ostala svojstva
4.1 Alternativna rekurzija
4.2 Verižni razlomci za Catalanove brojeve
4.3 Veza s Pascalovim trokutom
5. Literatura
1. Uvod
Na ove zanimljive brojeve prvi su naišli Leonhard Euler (1703.-1783.) i Johann Andreas von Segner (1704.-1777.), gotovo čitavo stoljeće prije Catalana (1814.-1894.). Proučavajući problem triangulacije konveksnog n-terokuta, Segner je postavio rekurzivnu relaciju, a Euler prvi uspješno riješio i 1760. godine došao do općeg izraza za broj triangulacija. Zanimljivo je napomenuti kako je Euler problemu pristupio alatima koji se pripisuju modernoj kombinatorici, izračunavši tako funkciju izvodnicu za broj triangulacija i zatvorenu formulu iz nje. Ipak, u čast Catalanu, koji je izveo i dokazao mnoga svojstva i identitete ovih brojeva, oni se danas zovu njegovim imenom. Catalanovi brojevi javljaju se u mnoštvu naizgled nepovezanih kombinatornih problema. U knjizi [11] ih se navodi čak 95. Malo je poznato da je ove brojevi potpuno neovisno otkrio kineski matematičar Ming An-Tu (1692.-1763.) tijekom 1730-ih godina, no njegovi radovi ostali su nepoznati zapadnom svijetu sve do 1839. godine.
|
2. Problemi vezani uz Catalanove brojeve
2.1 Triangulacija konveksnog n-terokuta
Ovaj povijesno najstariji problem doveo je do otkrića
Catalanovih brojeva. Razmatra se broj načina (označimo taj
broj s Tn) na koji je moguća maksimalna dekompozicija
konveksnog n-terokuta na
Razmotrimo problem induktivno i počnimo s trokutom.
S obzirom da je on već trianguliran, postoji samo jedan način
triangulacije pa je stoga T3 = 1. Za konveksan četverokut (n = 4) moramo povući jednu dijagonalu. To možemo
učiniti na dva načina (jer takav četverokut
ima dvije dijagonale) pa je, dakle, T4 = 2. Za peterokut (n = 5) rješenje je manje očigledno, postoji 5
načina triangulacije. Nađimo sad opće rješenje za broj
triangulacija n-terokuta Tn. Primijetimo da je svaka stranica
Za prebrojavanje koristit ćemo rekurziju i sljedeći algoritam - nasumce odabiremo i fiksiramo jednu od stranica te brojimo triangulacije u kojima sudjeluje svaki od trokuta podignutih nad tom stranicom. Za k-tu točku kao vrh trokuta, zdesna je ostao (n - k + 1)-terokut, koji možemo triangulirati na Tn-k+1 načina, a s lijeva k-terokut koji možemo triangulirati na Tk načina (vidi sliku 1). Pritom podrazumijevamo da je T2 = 1.

Slika 1: Fiksiramo jednu stranicu i nad njom konstruiramo trokute.
Budući da su izbori triangulacije izdvojenih mnogokuta međusobno neovisni, vrijedi kombinatorni princip produkta te je za odabranu točku k taj broj jednak TkTn-k+1. Izbor te točke također možemo učiniti na više (neovisnih) načina pa nam preostaje još samo prosumirati po svim mogućim vrijednostima k. Konačan oblik za Tn glasi:
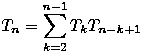
Pomoću programskog paketa Mathematica skicirat ćemo triangulacije nekih konveksnih poligona na sljedeći način:
<<DiscreteMath‘Combinatorica‘
sup[{p_,q_}, n_] := Abs[p-q]>1&&p<q&&Mod[p+1, n]!=q&&Mod[q+1,n]!=p;
intersect[{___,{a_, b_},___,{c_, d_},___}/;(a<c<b<d||c<a<d<b)]:=True;
triangulate[n_]:=ShowGraphArray[FromUnorderedPairs/@Map[Join[
ToUnorderedPairs[Cycle[n]],#]&,DeleteCases[Subsets[Select[
Tuples[Range[n], 2], sup[#, n] &], {n - 3}], _?intersect]]]
Do[triangulate[i], {i, 3, 6}]
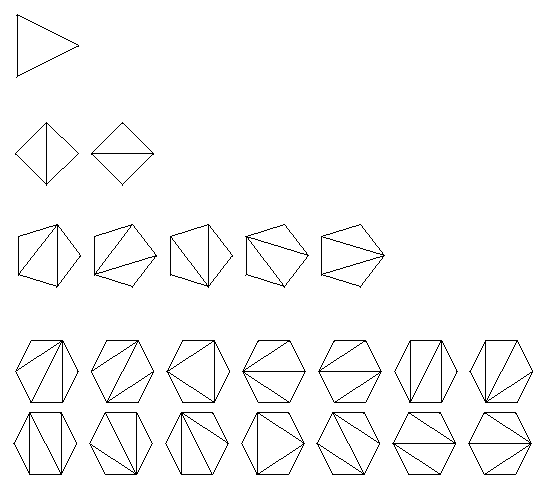
Slika 2: Triangulacije nekih poligona.
Definirali smo funkciju sup koja provjerava jesu li vrhovi p i q susjedni i vraća logički istinitu vrijednost
ako nisu. Funkcija intersect prima listu uređenih parova vrhova
(tj. dijagonale) kao argument i testira sadrži li ona dijagonale
koje se sijeku te vraća logički istinitu vrijednost ako
lista nije valjana. Definiramo funkciju triangulate koja prikazuje triangulirane
poligone. Najprije generiramo sve moguće uređene parove prirodnih
brojeva manjih ili jednakih n, zatim odaberemo one koji su dijagonale i od takvih
odabiremo sve moguće n- 3 podskupove (jer do kraja triangulirani poligoni imaju
točno toliko dijagonala). Još nam preostaje od njih pomoću
funkcije DeleteCases odabrati valjane poligone kojima
se dijagonale ne sijeku, funkcijom Join pridružiti im obodne lukove (Cycle[n]) te ih prikazati pomoću ShowGraphArray. Mnoštvo višestrukih
odabira navodi nas na zaključak da su ovom metodom grafovi prošli
"sito i rešeto" prije nego li su zadovoljili sve kriterije. Postoji
li neka druga metoda kojom bismo efikasnije pronašli tražene grafove?
Možemo potražiti bijekciju s nekim drugim problemom koji također vodi na Catalanove brojeve te tako doći do drugog načina generiranja triangulacija. Kao primjer, uspostavit ćemo bijekciju s problemom redoslijeda množenja (o kojem će biti riječi u idućoj cjelini) na način kako je prikazano na slici 3.
Slika 3: Bijekcija s problemom redoslijeda množenja
2.2 Redoslijed množenja
Na koliko načina možemo pomnožiti n brojeva, ne mijenjajući pritom poredak brojeva, već samo redoslijed množenja? Množenje je binarna operacija pa od zadanih n brojeva prvo moramo pomnožiti dva, zatim njihov umnožak množiti narednim elementom i tako redom dok svi brojevi ne budu pomnoženi. Da eksplicitno prikažemo redoslijed množenja, koristit ćemo zagrade.
Pritom moramo paziti na to da zagrade ne možemo postaviti bilo kako - zagrađujemo parove brojeva pa se unutar jednog para zagrada ne mogu nalaziti npr. četiri ili samo jedan broj. Na koliko načina to možemo učiniti za niz duljine n? Taj broj ćemo označiti sa Zn.
Valja odmah uočiti da nisu važni sami brojevi ni njihov odnos i da je jedino poredak zagrada bitan. Zbog toga ih možemo zamijeniti nekom oznakom, a u kasnijem razmatranju i ispustiti. Krenimo od početka - jasno je da (gledajući poredak svih zagrada s lijeva na desno) ne možemo započeti sa zatvorenom zagradom, već prva zagrada mora biti otvorena. Sljedeća može biti otvorena ili zatvorena, iduća pak zatvorena samo ako prethodna nije bila, itd.
Riješit ćemo ovaj primjer sagledavši očitu činjenicu - da bismo dobili konačan rezultat množenja, moramo pomnožiti neka dva zagrađena bloka. Štoviše, ti blokovi ne mogu biti raštrkani, već jedan mora biti na početku, a drugi na kraju niza brojeva koje množimo (presjek skupova omeđenih zagradama mora biti disjunktan).
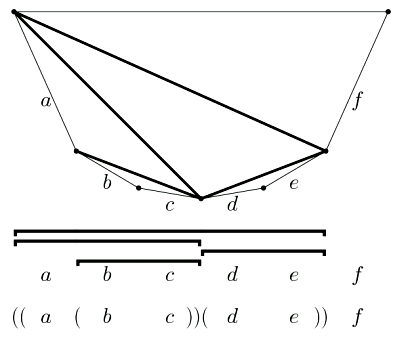
Odaberemo li prvi blok duljine k, drugi mora biti duljine n - k. Prvi stoga možemo zagraditi na Zk, a drugi blok na Zn-k načina i to nezavisno jedan od drugoga. Prema pravilu produkta, ako je duljina prvog bloka k, imamo ZkZn-k načina zagrađivanja; uočite sličnost s prethodnim primjerom! Još nam preostaje prosumirati po svim mogućim vrijednostima k. Primijetite, k ne poprima vrijednosti veće od 1 ni one manje od n - 1 zato što blokovi moraju biti neprazni. Konačno, traženi izraz glasi:
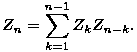
Nekoliko početnih vrijednosti brojeva Zn su: Z1 = 1,Z2 = 1,Z3 = 2,Z4 = 5...
Generirat ćemo sve moguće rasporede zagrada za n=4 pomoću programskog paketa Mathematica na sljedeći način:
rule:={a___,b_,c_,d___}->{a,{b,c},d}
cl[L_List]:= Union[Nest[Flatten[Map[ReplaceList[
#,rule]&,#],1]&,{L},Length[L]-2]]
cl[Range[4]]
Out[1]={{1,{2,{3,4}}},{1,{{2,3},4}},{{1,2},{3,4}},
{{1,{2,3}},4},{{{1,2},3},4}}
2.3 Problem zagrađivanja
Problem zagrađivanja vrlo je sličan problemu redoslijeda množenja. Postavlja se pitanje na koliko načina možemo u nizu rasporediti 2n zagrada tako da, brojeći s lijeva, ni u jednom trenutku ne nabrojimo (strogo) više zatvorenih nego otvorenih zagrada. Na primjer, zagrađivanje ()() je valjano, a ())( nije jer na poziciji 3 primjećujemo veći broj zatvorenih nego otvorenih zagrada. Da bismo dokazali istovjetnost s prethodnim problemom, uspostavimo bijekciju na sljedeći način: odstranimo sve osim zatvorenih zagrada i znakova množenja, koje zatim zamijenimo otvorenim zagradama.
Problem je također ekvivalentan broju mogućih valjanih ugniježđenja n blokova u nekim programskim jezicima (na primjer, u programskom jeziku C). Točnije, prebrojavamo valjane rasporede n parova zagrada koji omeđuju blokove.
Generirat ćemo takve parove zagrada pomoću programskog paketa Mathematica:
cat[n_Integer?Positive] := Select[IntegerDigits[Range[2^n], 2, n],
VectorQ[Most@FoldList[Plus, 0, # /. 0 -> -1], NonNegative] &&
Tr@# == n/2 &]
TableForm[cat@6/.{1->"(",0->")"},TableSpacing->{1,0}]
()()()
()(())
(())()
(()())
((()))
Pomoću funkcije IntegerDigits generiramo sve moguće liste jedinica i nula duljine n. Koristeći Select, odabiremo liste koje nam odgovaraju: prvo zahtijevamo da lista ima jednak broj nula i jedinica, što možemo jednostavno postići shvaćajući listu kao vektor, uvjetom da njegov trag (funkcija Tr) bude n/2. Budući da je Catalanov broj također i broj nenegativnih parcijalnih suma jednakog broja jedinica i minus jedinica, računamo parcijalne sume elemenata liste funkcijom FoldList, prethodno zamijenivši sve 0 u -1 te koristimo test VectorQ kako bismo uvjetovali da svaki od elemenata parcijalne sume mora zadovoljavati uvjet NonNegative. Tek tada čitav izraz može biti logički istinit, a konkretna lista odabrana.
2.4 Putovi u cjelobrojnoj mreži
Cjelobrojnu mrežu ili diskretnu rešetku tvore pravci kroz cjelobrojne točke, usporedni s koordinatnim osima u Kartezijevom koordinatnom sustavu. Za ovaj konkretan primjer uvodimo restrikciju na mrežu veličine n × n te se pitamo koliko ima najkraćih putova u ovakvoj cjelobrojnoj mreži koji nikad ne prelaze njezinu dijagonalu. Taj broj označit ćemo s Pn. Bez smanjenja općenitosti možemo promatrati putove koji su uvijek ispod nje.
Podsjetimo se, najkraći putovi zadovoljavaju uvjet da se u svakom idućem koraku mora biti bliže odredišnoj točki te su u ovom primjeru stoga dopušteni jedino pomaci gore ili desno (krećemo iz ishodišta koordinatnog sustava). Valja uočiti da je ovaj problem ekvivalentan prethodnom problemu postavljanja zagrada - svaki
odmak od dijagonale udesno možemo zapisati otvorenom zagradom, a pomak gore, prema dijagonali,
zatvorenom.
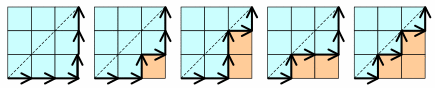
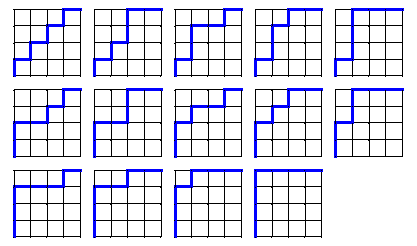
Slika 4: Putovi u cjelobrojnoj mreži 3 x 3 [12]
Pokušajmo direktno prebrojiti ovakve putove i time dobiti eksplicitnu
formulu za n-ti Catalanov broj. Prvo prebrojimo sve putove kroz cjelobrojnu
mrežu do točke (n,n) i od tog broja oduzmemo broj zabranjenih putova koji sijeku dijagonalu. Svaki cjelobrojni put
možemo kodirati određenim redoslijedom vektora pomaka udesno
(1, 0) i vektora pomaka prema gore (0, 1). Izbor pozicija pomaka prema gore (od ukupnog broja od 2n pomaka) jednoznačno određuje put u cjelobrojnoj mreži jer preostale pozicije predstavljaju pomake udesno. Pomake prema gore možemo rasporediti na 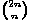 načina.
načina.
Izbrojimo sad putove koji sijeku dijagonalu. Promatramo prvu
točku na nedozvoljenom putu koja se nalazi s krive strane dijagonale. Nakon te točke reflektiramo put na način da svaki pomak udesno zamijenimo pomakom prema gore i obrnuto.
Budući da smo došli jedno polje iznad dijagonale, dosad smo učinili k pomaka prema desno i k + 1 prema gore. Preostalo nam je n - k pomaka desno i n - k - 1 pomaka gore da bismo došli do (n,n). Reflektiranjem puta zamjenjuju se brojevi preostalih pomaka
pa će takva modificirana staza imati k + (n - k - 1) = n - 1 pomaka udesno i (k + 1) + (n - k) = n + 1 prema gore, dakle doći ćemo do točke (n - 1,n + 1). Svaki nedozvoljen put možemo tako modificirati na jedinstven način. Uočimo i da svaki najkraći put u cjelobrojnoj mreži od (0, 0) do (n - 1,n + 1) možemo preinačiti u točno jedan nedozvoljen put od (0, 0) do (n,n), reflektirajući ga na isti način čim prijeđe originalnu dijagonalu. Time smo uspostavili
bijekciju između skupa svih najkraćih putova koji sijeku dijagonalu i skupa svih najkraćih putova u cjelobrojnoj mreži do točke (n - 1,n + 1), kojih ima 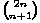 . Stoga je n-ti Catalanov broj jednak
. Stoga je n-ti Catalanov broj jednak
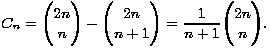
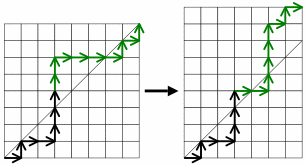
Slika 5: Reflektirani put [12]
Poslužit ćemo se programskim paketom Mathematica i nacrtati prvih nekoliko slučaja (vidljivih na slici 6) pomoću sljedećeg programskog koda:
<< DiscreteMath‘Combinatorica‘
gen[n_Integer?Positive] := Select[IntegerDigits[Range[2^n], 2, n],
VectorQ[Most@FoldList[Plus, 0, # /. 0 -> -1], NonNegative] &&
Tr@# == n/2 &]
spf[l_List] := Block[{x = 1, n = Length[l]/2 + 1}, Highlight[
GridGraph[n,n], {Partition[Join[{1}, Table[If[l[[i]] ==
1, (x = x + n), (x = x + 1)], {i, 1, Length[l + 1]}]], 2, 1]},
{HighlightedEdgeColors -> {Blue},
HighlightedEdgeStyle -> Thickness[0.05]}]];
For[i = 2, i < 12, i = i + 2; ShowGraphArray[Partition[
spf /@ gen@i, 5, 5, {1, 1}, {}]]]
2 x 2

3 x 3
4 x 4

5 x 5
Slika 6. Najkraći putovi koji ne prelaze dijagonalu
Najprije definiramo funkciju gen koja generira liste jedinica i nula duljine 2n, uz uvjet da ni u jednom trenutku broj nula ne premaši broj jedinica. Ovako dobivene liste interpretirat ćemo kao kodirane pomake - jedinice će predstavljati pomake prema gore, a nule pomake u smjeru desno. Da bismo što jednostavnije nacrtali željeni graf, generirat ćemo cjelobrojnu mrežu funkcijom GridGraph te potom funkcijom Highlight označiti željene putove. Iz već spomenute liste pomaka generiramo listu obilaska grafa, uzevši u obzir konkretnu numeraciju pojedinih čvorova. Radi li se o pomaku udesno, trenutačni čvor uvećamo za jedan, a u slučaju pomaka prema gore povećanjem trenutačnog indeksa za n + 1 dobijamo broj koji odgovara elementu na istoj poziciji u retku iznad. Naposljetku, funkcijom Partition dobiven redoslijed čvorova rastavljamo u 2-particije koje za funkciju Highlight predstavljaju lukove grafa koje treba istaknuti.
2.5 Dyckovi planinski putovi
Koliko ima različitih konfiguracija planinskih lanaca s točno 2n uspona (ili padova)? Označimo taj broj s Dn. Ispravna konfiguracija Dyckovog puta podrazumijeva da je visina uvijek nenegativna, tj. da broj uspona u svakom trenutku mora biti veći ili jednak broju padova.

Slika 7. Dyckovi planinski putovi za n = 4
Primijetimo analogiju s problemom zagrađivanja, gdje broj zatvorenih zagrada prije pozicije k ne smije premašiti broj otvorenih prije iste pozicije. Bijekciju uspostavljamo na način da svaku otvorenu zagradu zamjenjujemo usponom, a zatvorenu padom. Također, lako je uvidjeti da je ovaj problem vizualno sličan i matematički potpuno ekvivalentan prethodnom, a graf jednog možemo dobiti iz grafa drugog rotacijom; stoga zaključujemo da je Dn = Pn.
Prikažimo to u Mathematici:
<< DiscreteMath‘Combinatorica‘
gen[n_Integer?Positive] := Select[IntegerDigits[Range[2^n], 2, n],
VectorQ[Most@FoldList[Plus, 0, # /. 0 -> -1], NonNegative] &&
Tr@# == n/2 &]
pf[l_List] := Block[{x = 1, n = Length[l]/2 + 1}, Highlight[
RotateVertices[GridGraph[n,n], -Pi/4], {Partition[Join[{1},
Table[If[l[[i]] == 1, (x = x + n), (x = x + 1)], {i, 1,
Length[l + 1]}]], 2, 1]}, {HighlightedEdgeColors -> {Blue},
HighlightedEdgeStyle -> Thickness[0.05]}]];
For[i = 2, i < 12, i = i + 2; ShowGraphArray[Partition[pf /@ gen@i, 6, 6,
{1, 1}, {}], EdgeColor->White, VertexStyle->{None}]]
Koristimo gotovo istovjetan kod, uz dodatak funkcije RotateVertices, kojom graf rotiramo za -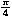 . Također, cjelobrojnu rešetku isključujemo postavljanjem opcije EdgeColor u White.
. Također, cjelobrojnu rešetku isključujemo postavljanjem opcije EdgeColor u White.
2.6 Problem rukovanja
Na koliko se načina 2n ljudi raspoređenih oko okruglog stola može rukovati tako da im se ruke ne križaju? I ovaj je problem ekvivalentan ostalima te je rješenje ponovno Catalanov broj Cn. Dokažimo to - bijekciju ćemo uspostaviti npr. s problemom zagrada, tako da svaku od zagrada numeriramo brojevima od 1 do 2n te na isti način po redu označimo vrhove grafa. Zatim postupamo na sljedeći način: pronađemo par zagrada (otvorenu i zatvorenu) unutar kojih nema drugih zagrada, te spojimo pripadajuće vrhove grafa. Taj par izbacimo i postupak nastavimo sve dok ne izbacimo i zadnji par zagrada. Na taj način konstruirali smo bijekciju između ovih dvaju problema jer je za svaki raspored zagrada moguće jednoznačno konstruirati pripadajući graf rukovanja. Nacrtajmo to pomoću programskog paketa Mathematica:
<< DiscreteMath`Combinatorica`
cat[n_Integer?Positive] := Select[IntegerDigits[Range[2^n], 2, n],
VectorQ[Most@FoldList[Plus, 0, # /. 0 -> -1], NonNegative] &&
Tr@# == n/2 &]
handshake[n_Integer] := ShowGraphArray[Partition[FromUnorderedPairs/@
Flatten[{Table[{cat[n][[i]][[j]],j},{i,1,Length[cat[n]]},{j,1,n}]
//.{x___, {1,p_}, {0,q_}, y___}->{x,y,{p,q}}},1],k=Ceiling[Sqrt[
Length[cat[n]]]],k,{1,1},{}],AspectRatio->Automatic,VertexStyle->
Disk[0.1],VertexColor->Green]
Do[handshake[2i],{i,5}]
n = 2
n = 4
n = 6
n = 8
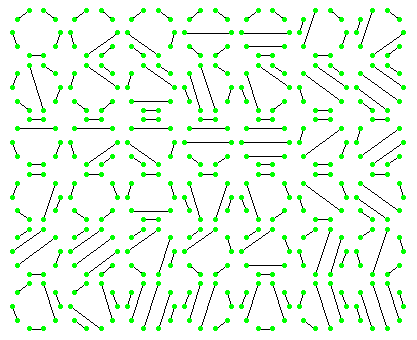
n = 10
Slika 8. Grafovi rukovanja
Ravnajući se kombinatornim dokazom o bijektivnosti s problemom
zagrada, postupamo na sljedeći način. Funkcijom cat generiramo inicijalne liste nula i jedinica uz uvjet da
broj nula ni u jednom trenutku ne smije premašiti broj jedinica (njih možemo shvatiti kao otvorene, a nule kao zatvorene zagrade). Iz tih
lista pomoću funkcije Table tvorimo liste uređenih parova koje čine element inicijalne liste i njegov redni broj. Zatim primjenjujemo algoritam korišten u bijektivnom dokazu - primjenom operacije ReplaceRepeated (u skraćenom obliku //.) tražimo uzastopne parove jedinica i nula te svaki takav pronađeni par uređenih parova
sjedinjujemo u jedan uređeni par koji sačinjavaju redni brojevi polaznih parova i stavljamo na
kraj liste.
Na taj način elementi s kraja liste neće smetati uzastopnoj primjeni operacije ReplaceRepeated te ćemo naposljetku dobiti listu koja sadrži parove oznaka čvorova, tj. ljudi koji se rukuju. Još ih samo treba spojiti i nacrtati, što ćemo najlakše učiniti pomoću funkcije FromUnorderedPairs, koja čini upravo to - crta graf čiju je listu spojnica primila kao argument. Za olakšan prikaz particionirat ćemo izlazne podatke (tipa Graph) u podskupove s brojem elemenata približno jednakim korijenu duljine početne liste. Na taj ćemo način pomoću funkcije ShowGraphArray pokazati sve grafove određenog slučaja odjednom, na slici koja je približno kvadratnog formata.
U teoriji grafova stablo se definira kao povezan graf u kojem
nema ciklusa. Binarno stablo sačinjava jedan istaknuti vrh koji se naziva korijenom, i uređeni par binarnih
stabala koja se nazivaju lijevim i desnim podstablom (podstabla mogu biti prazna). Postavlja se pitanje: koliko ima različitih binarnih stabala s n vrhova? Označimo traženi broj s Bn. Možemo brojati ovako - "razrežemo" stablo između korijena i podstabala te brojimo njihove moguće konfiguracije. U lijevom može biti jedan vrh, a u desnom n- 2 ili pak u lijevom dva, a u desnom n- 3, itd. U općem slučaju, u lijevom može biti k vrhova, a u desnom n - k - 1 pa lijevih podstabala ima Bk, a desnih Bn-k-1. Slučaji su neovisni pa prema pravilu produkta ukupni
broj konfiguracija za čvrsto k iznosi BkBn-k-1. Sumiramo po svim vrijednostima k i dobivamo već poznati rezultat:
Navedimo nekoliko početnih vrijednosti broja Bn: B0 := 1,B1 = 1,B2 = 2,B3 = 5... Nacrtajmo sada nekoliko slučaja pomoću programskog
paketa Mathematica (uz prethodnu preinaku funkcije TreePlot paketa DiscreteMath‘Tree‘ kako bi stabla izgledala ljepše):
n = 2 n = 3
n = 4 n = 5 Budući da su rekurzivni algoritmi naročito pogodni za stabla, riješit ćemo problem takvim algoritmom. Prvo definiramo uvjete izlaska iz rekurzije,
a zatim i samu rekurzivnu funkciju ct, kojom generiramo sve moguće konfiguracije binarnih stabala sa zadanim brojevima čvorova. Koristimo funkciju TreePlot iz paketa DiscreteMath‘Tree‘, koji tip podataka Tree definira kao listu s tri podliste, od kojih je prva uređen par
oznake i rednog broja čvora, a druga i treća predstavljaju lijevo i desno podstablo. Ako generiramo
binarna stabla u tom formatu, možemo ih jednostavno crtati pozivom funkcije TreePlot. Pogledajmo kako izgleda izlaz funkcije za stablo s četiri vrha, u formatu MatrixForm: Sve što nam preostaje jest pozvati funkciju TreePlot za svaku konfiguraciju stabala te prikazati skup rezultata kao polje grafičkih elemenata GraphicsArray. Možemo još pokušati ravnomjerno rasporediti grafove (u kvadrat) tako da
ih particioniramo u podskupove kojima je duljina približno korijen ukupne duljine liste, što postižemo kombinacijom funkcija Sqrt i Floor.
Na prethodnim primjerima (ponegdje uz pomak indeksa) uvidjeli
smo da se zapravo radi o istoj rekurziji, koja glasi ovako: Kada bismo na neki način uspjeli pronaći funkciju kojoj razvoj u formalni red potencija kao koeficijente uz x ima niz Catalanovih brojeva, znali bismo kako glasi njihova
opća formula.
Budući da je rekurzija za Cn potpune prošlosti (tj. da bismo izračunali njen opći
član, nije dovoljno računati s nekoliko prethodnih članova, već moramo uzeti u
obzir sve), ne možemo je jednostavno riješiti. Ipak, možemo se njome poslužiti da dobijemo funkcionalnu jednadžbu rješavanjem koje bismo izveli traženu funkciju, a potom je razviti u red potencija i pronaći zatvorenu formulu za Cn.
Poslužit ćemo se malim trikom i kvadrirati prethodni izraz.
2.7 Problem binarnih stabala
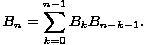

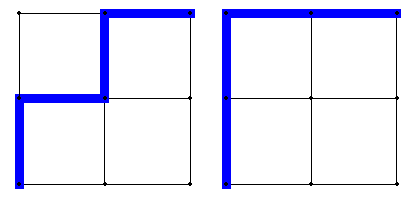
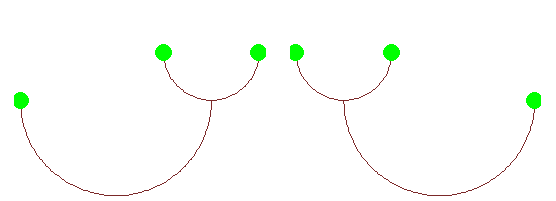
Slika 9: Binarna stabla s tri
čvora [12]
<<DiscreteMath‘Tree‘
ct[{}]:={{}}
ct[{a_}]:={{0,a}}
ct[l_List]:=
Module[{i,m=Rest[l],elem1st=First[l]}, Join@@Map[Insert[#,{0,elem1st},{1}]&,
Table[Distribute[{ct[Take[m,i]],ct[Take[m,{i+1,Length[m]}]]},List],{i,0,
Length[m]}],{2}]]
For[k = 2, k <= 6, k++, Show[GraphicsArray[
Partition[a = TreePlot /@ ct[Range[k]], f = Floor[Sqrt[Length[a]]],
f, {1, 1}, {}], AspectRatio -> Automatic]]]

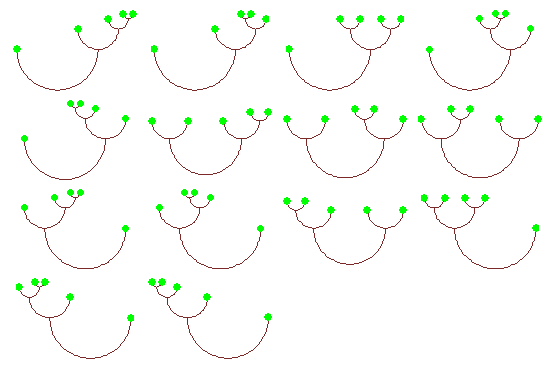
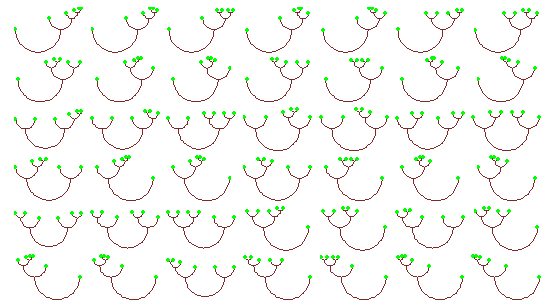
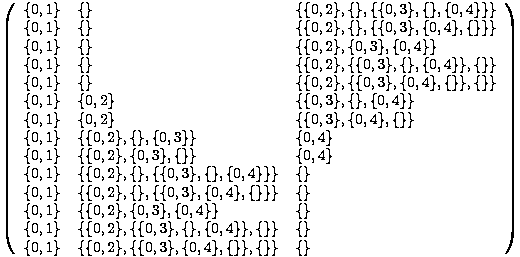
3. Funkcija izvodnica za Catalanove brojeve
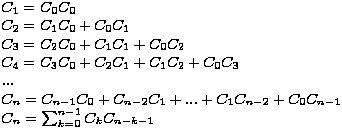
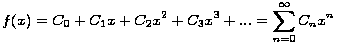
![[f(x)]2 = C0C0+ (C1C0+ C0C1)x +(C2C0 +C1C1 + C0C2)x2+ ...](catalan2419x.png.gif)
Pogledajmo još jednom gornji niz rekurzija - koeficijenti u zagradama koje smo dobili kvadriranjem izraza upravo su Catalanovi brojevi pa ćemo ih tako i izraziti.
![[f(x)]2 = C + C x +C x2 +C x3 +...
1 2 3 4](catalan2420x.png.gif)
Primjećujemo da indeksi koeficijenata ne odgovaraju potencijama od x, što možemo popraviti množenjem cijelog izraza s x.
![x .[f(x)]2 = C x +C x2 +C x3 +C x4 +...
1 2 3 4](catalan2421x.png.gif)
Gornjem izrazu nedostaje još samo član C0, koji je jednak 1, pa dodavanjem jedinice dobivamo sljedeću funkcionalnu jednadžbu, koju sređujemo i rješavamo po f(x):
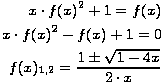
Koje je rješenje ove kvadratne funkcionalne jednadžbe ispravno? Znamo da mora vrijediti f(0) = C0 = 1 pa iskoristimo taj uvjet i izraz ocijenimo prijelazom na limes.
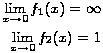
Još nam preostaje razviti dobivenu funkciju u red potencija kako bismo dobili izraz za pripadajuće koeficijente u zatvorenom obliku. Pritom ćemo za razvijanje izraza koristiti binomni red.
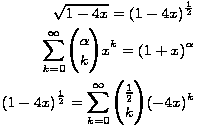
Prvo računamo opći binomni koeficijent 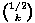 :
:
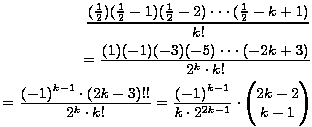
Zato vrijedi
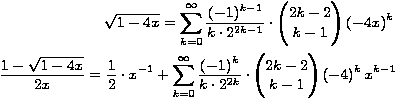
Na kraju nalazimo koeficijent uz xn, koji predstavlja traženu formulu za C n:
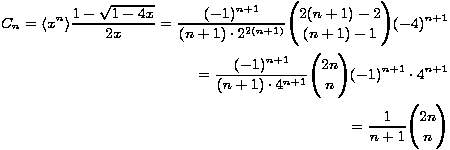
Zanimljivo je promotriti kako se opći izraz za n-ti Catalanov broj ponaša kada n teži u beskonačnost. Da bismo to pokazali, poslužit ćemo se Stirlingovom aproksimacijskom formulom:
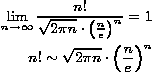
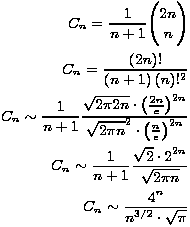
4. Ostala svojstva
4.1 Alternativna rekurzija
Dokažimo još jednu rekurzivnu relaciju za Catalanove brojeve. Promatrajmo uređene parove koje čine triangulacija (n+2)-terokuta i jedna njezina istaknuta dijagonala. Ako prvo izaberemo trijangulaciju, zaključujemo da takvih parova ima Cn . (n- 1) (jer je Cn = Tn+2 i izabrana trijangulacija sadrži n-1 dijagonala). S druge strane, možemo prvo izabrati dijagonalu. Točno n + 2 dijagonala odsjecaju od našeg mnogokuta (k+2)-terokut. Ako fiksiramo jednu, postoji CkCn-k triangulacija koje je sadrže. Svaki par brojali smo dvaput (za (k+2)-terokut i za (n-k+2)-terokut) pa izraz moramo podijeliti s 2:
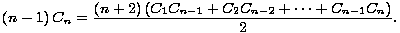
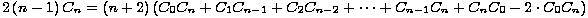
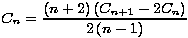
Iz toga jednostavno slijedi da je 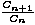 =
= 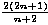 .
.
Algebarski, možemo to raspisati i ovako:
![C (2n +2)! (n+ 1)(n!)2
Cn+1= (n-+2)[(n-+-1)!]2---(2n)!---
n
= (2n+-2)(2n-+1)(n+2-1)
(n +2)(n+ 1) 2
= 2(2n-+-1)(n-+1)--
(n + 1)2(n+ 2)
= 2(2n+-1)
n+ 2
C = 2(2n+-1).C
n+1 n + 2 n](catalan2437x.png.gif)
Rješavanjem ove rekurzije dobivamo sljedeći izraz za n-ti Catalanov broj:
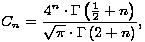
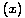 gama funkcija definirana s
gama funkcija definirana s 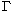
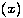 =
= 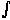 0
0 tx-1e-tdt. Rezultat možemo zapisati na ovaj krajnje neobičan način (dakako, on ima kombinatorni smisao samo za prirodne brojeve):
tx-1e-tdt. Rezultat možemo zapisati na ovaj krajnje neobičan način (dakako, on ima kombinatorni smisao samo za prirodne brojeve):
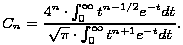
Također, ako ocijenimo omjer 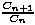 =
= 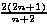 limesom kad n teži u beskonačnost, vidimo da omjer susjednih članova niza Catalanovih brojeva teži broju 4 pa je Cn+1 za jako velike n približno 4 puta veći od Cn.
limesom kad n teži u beskonačnost, vidimo da omjer susjednih članova niza Catalanovih brojeva teži broju 4 pa je Cn+1 za jako velike n približno 4 puta veći od Cn.
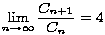
4.2 Verižni razlomci za Catalanove brojeve
Da bismo pokazali vezu Catalanovih brojeva s verižnim razlomcima, poslužit ćemo se već izvedenom funkcionalnom jednadžbom
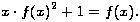
Pregrupirajmo izraz i izlučimo f(x)...
![f(x).[1- x.f(x)]= 1](catalan2446x.png.gif)
...te zatim podijelimo faktorom u zagradi kako bismo izrazili f(x).
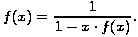
Odatle iterativnim uvrštavanjem gornjeg izraza za f(x) u nazivnik dobivamo verižni razlomak
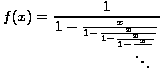
Kao primjer, provjerimo to razvojem u red potencija funkcije koju dobijemo nakon nekoliko iteracija verižnog razlomka, služeći se pritom programskim paketom Mathematica:
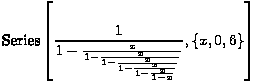
![2 3 4 5 6 7
1 +x + 2x +5x + 14x + 42x + 132x + O[x].](catalan2450x.png.gif)
Uočimo da su koeficijenti u ovom razvoju upravo Catalanovi brojevi.
4.3 Veza s Pascalovim trokutom
Jednu takvu vezu već smo pronašli izvodeći broj putova u cjelobrojnoj mreži. Pokazali smo kako je n-ti Catalanov broj jednak
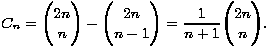
To je upravo razlika srednjeg člana i njemu susjednog elementa parnog retka. Što je s neparnim redcima? Kod njih oduzimamo jedan od srednjih članova i njemu susjedni s iste strane. Primijetimo da zapravo radimo istu stvar. Budući da je svaki element Pascalova trokuta suma elemenata u retku iznad njega s lijeve i desne
strane, tako je 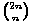 zapravo 2 .
zapravo 2 .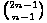 (pravilo apsorpcije binomnih koeficijenata). Također, vrijedi
(pravilo apsorpcije binomnih koeficijenata). Također, vrijedi
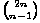 =
= 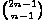 +
+ 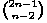 pa dobivamo:
pa dobivamo:
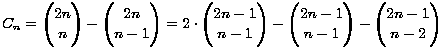
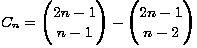
Postoje i druge veze Catalanovih brojeva s Pascalovim trokutom. Neke
od njih je jednostavno uočiti, a druge uopće ne bismo očekivali. Jednostavno je uočiti da se npr. Catalanovi brojevi pojavljuju kao faktori srednjih članova parnih redaka. Uistinu, nekoliko prvih srednjih
članova su redom: 1 = 1 . 1, 2 = 1 . 2, 6 = 2 . 3, 20 = 5 . 4, 70 = 14 . 5, 252 = 42 . 6, 924 = 132 . 7.... Budući da je Cn = 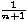
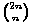 , množenjem jednakosti s n + 1 uviđamo da je srednji član uistinu jednak umnošku n-tog Catalanovog broja i faktora n + 1.
, množenjem jednakosti s n + 1 uviđamo da je srednji član uistinu jednak umnošku n-tog Catalanovog broja i faktora n + 1.
Još jednu vezu možemo pronaći ovako. Krenimo od izraza
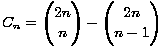
Uzastopnom primjenom jednakosti  =
= 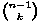 +
+ 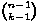 na posljednjem članu dobivamo sljedeći izraz, koji predstavlja razliku srednjeg elementa
na posljednjem članu dobivamo sljedeći izraz, koji predstavlja razliku srednjeg elementa
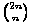 i svih elemenata na dijagonali Pascalovog trokuta:
i svih elemenata na dijagonali Pascalovog trokuta:
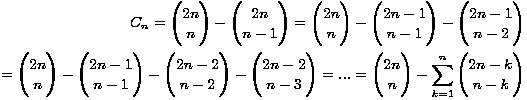
 |
5. Literatura
[1] Davis, T., Catalan Numbers, http://www.geometer.org/mathcircles, 2001.
[2] Fomin, S., Reading, N., Root systems and generalized associahedra, IAS/Park City Mathematics Institute, 2004.
[3] Gardner, M., Mathematical games, Catalan numbers: an integer sequence that materializes in unexpected places, Scientific American, 1976.
[4] Graham, L., Knuth, D., Patashnik, O., Concrete Mathematics: a foundation for computer science, Addison-Wesley, New York, 1989.
[5] Mahendra J., Rieper, R.G., Continued fractions and Catalan problems, 2000.
[6] Merris, R., Combinatorics, 2nd ed., John Wiley and Sons, 2003.
[7] Rosas, M.H., Los Numeros de (Euler)-Catalan, Boletin de la Asociacion Matematica Venezolana, Vol X, No.1, 2003.
[8] Rosen, K.H., Discrete Mathematics and Its Applications, McGraw-Hill, 1998.
[9] Sloane, N., On-line encyclopedia of integer sequences, http://www.research.att.com/~njas/sequences
[10] Stanley, R.P., Enumerative Combinatorics I, Wadsworth, Monterey, California, 1986.
[11] Stanley, R.P., Enumerative Combinatorics Vol. 2, Cambridge University Press, Cambridge, 1999.
[12] Wikipedia: The Free Encyclopedia (veljača 2006.), Catalan number. http://en.wikipedia.org/wiki/Catalan_number
[13] Wilf, H.S., Generatingfunctionology, Academic Press, 1994.
[14] Wolfram, S., The Mathematica Book, 5th ed., Wolfram Media, 2003.
1. Uvod
2. Problemi vezani uz Catalanove brojeve
2.1 Triangulacija konveksnog n-terokuta
2.2 Redoslijed množenja
2.3 Problem zagrađivanja
2.4 Putovi u cjelobrojnoj mreži
2.5 Dyckovi planinski putovi
2.6 Problem rukovanja
2.7 Problem binarnih stabala
3. Funkcija izvodnica za Catalanove brojeve
4. Ostala svojstva
4.1 Alternativna rekurzija
4.2 Verižni razlomci za Catalanove brojeve
4.3 Veza s Pascalovim trokutom
5. Literatura