
 |
Hrvatski matematički elektronski časopis math.e | |
| Broj 9 | ||
| http://web.math.hr/mathe/ |
Sadržaj:
1. Aritmetičko-geometrijska nejednakost
2. Dokazi AG nejednakosti
3. Primjene AG nejednakosti
Nejednakost između aritmetičke i geometrijske sredine, ili kraće AG nejednakost, svakako je jedna od najpoznatijih algebarskih nejednakosti. Radi se o usporedbi aritmetičke sredine
| An(a,w) = | w1a1 +...+ wnan |
| w1 +...+ wn |
i geometrijske sredine
| Gn(a,w) = ( a1w1 a2w2 ··· anwn) 1/Wn, |
pri čemu su a = (a1,...,an) i w = (w1,...,wn) uređene n-torke pozitivnih brojeva i Wn = w1+...+wn.
|
Teorem (AG nejednakost). Ako su a i w uređene n-torke pozitivnih brojeva, tada vrijedi An(a,w) ≥ Gn(a,w). Jednakost se postiže ako i samo ako je a1 = a2 = ... = an. |
U literaturi se mogu naći deseci različitih dokaza ove nejednakosti, a mi ćemo promotriti razne vizualne dokaze AG nejednakosti za n = 2 s jednakim težinama, tj. razmotrit ćemo dokaze nejednakosti
| (1) |
koja vrijedi za svaka dva pozitivna realna broja a i b. Jednakost se postiže ako i samo ako je a = b.
Prvo promotrimo algebarski dokaz nejednakosti (1).
Za svaka dva pozitivna broja a i b očito vrijedi nejednakost (√a − √b)2 ≥ 0, pri čemu jednakost vrijedi ako i samo ako je a = b. Kvadriranjem binoma i daljnjim transformacijama dobivamo
tj.
| a + b | ≥ √ab. |
| 2 |
Promotrimo sada nekoliko geometrijskih dokaza nejednakosti (1).
Dokaz 1.
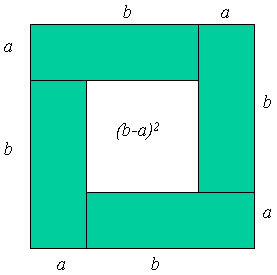
Veći kvadrat ima stranicu duljine a + b i njegova je površina očito veća od površine četiriju pravokutnika sa stranicama a i b (vidjeti sliku 1). Dakle, imamo
odakle slijedi nejednakost (1). Jednakost se postiže ako i samo ako je površina velikog kvadrata jednaka površini četiriju pravokutnika, odnosno ako i samo ako kvadrat u sredini figure iščezava, a to se događa ako i samo ako je b − a = 0.
Dokaz 2.
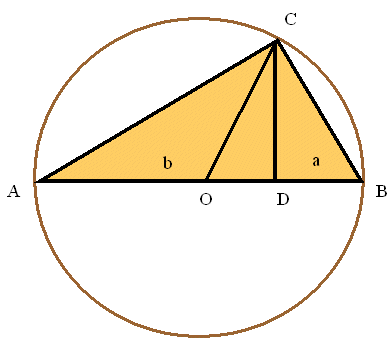
U pravokutnom trokutu ABC s hipotenuzom AB visina CD dijeli hipotenuzu na odsječke BD i DA duljina a i b (slika 2). Prema Euklidovu poučku, duljina visine na hipotenuzu jednaka je geometrijskoj sredini njenih duljina odsječaka na hipotenuzi, tj. |CD| = √ab.
S druge strane, polumjer kružnice opisane pravokutnom trokutu ABC jednak je polovini duljine hipotenuze, tj.
| |CO| = | a + b | . |
| 2 |
Budući da je u pravokutnom trokutu COD hipotenuza CO dulja od katete CD, slijedi nejednakost (1). Jednakost se postiže ako i samo ako trokut COD degenerira u dužinu CD, tj. ako i samo ako se težišnica CO podudara s visinom CD. To se događa ako i samo ako je trokut ABC jednakokračan, odnosno ako i samo ako su odsječci visine na hipotenuzi jednake duljine a = b.
Dokaz 3.
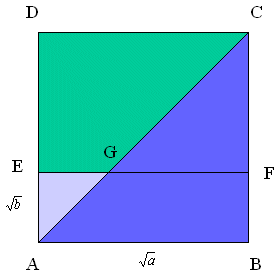
Kvadrat ABCD ima stranicu duljine √a, a pravokutnik ABFE ima stranice duljina √a i √b, b ≤ a. Sad imamo
| √ab | = | P(ABFE) | = | P(AGE) + P(ABFG) | ||||||
| ≤ | P(AGE) + P(ABC) | |||||||||
| = |
|
Time je ponovno dokazana AG nejednakost (1).
Dokaz 4.
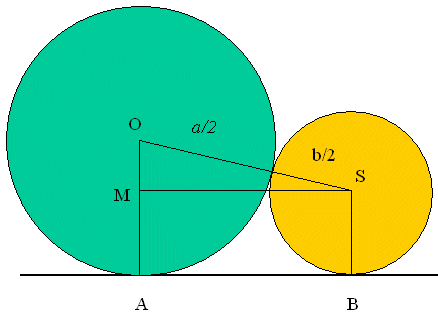
Neka su dane kružnice središta O i S te polumjera a/2 i b/2, a ≥ b, koje se diraju izvana, te neka je AB zajednička vanjska tangenta tih dviju kružnica. Točke A i B su dirališta tangente i kružnica. Trapez ABSO ima dva prava kuta pri vrhovima A i B. Neka je dužina SM paralelna s AB. Tada je trokut OMS pravokutan.
Hipotenuza OS ima duljinu (a + b)/2, a kateta OM ima duljinu (a − b)/2. Prema Pitagorinu poučku imamo
| ||||||||||||||||
| |SM| = | = √ab. | |||||||||||||||
Budući da je u pravokutnom trokutu hipotenuza dulja od katete, slijedi valjanost nejednakosti (1).
Dokaz 5.
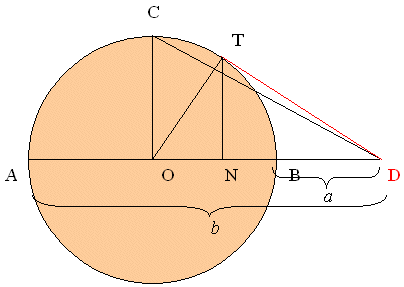
Neka je dana kružnica s promjerom AB duljine b − a i središtem O. Točka D nalazi se na pravcu kroz A i B tako da je |AD| = b i točka B je između točaka A i D. Tada je |BD| = a. Iz točke D povučena je tangenta na kružnicu. Točka T je diralište te tangente i kružnice. U pravokutnom trokutu OTD hipotenuza ima duljinu |OD| = (a+b)/2, a duljinu katete TD možemo izračunati pomoću Pitagorina poučka:
| ||||||||||||||||
| |TD| = | = √ab. | |||||||||||||||
Budući da je hipotenuza dulja od katete, vrijedi AG nejednakost (1).
Inače, na ovoj slici pojavljuje se nejednakost još dviju sredina: kvadratne i harmonijske. Naime, ako je CO polumjer okomit na promjer AB, tada duljina hipotenuze CD iznosi
| ||||||||
| |CD| = | . | |||||||
Ovaj se izraz naziva kvadratnom sredinom brojeva a i b. Nadalje, ako je N nožište visine iz vrha T u pravokutnom trokutu OTD, tada iz sličnosti trokuta TND i OTD slijedi |ND| : |TD| = |TD| : |OD|, tj.
| |ND| = | 2ab | . |
| a + b |
Ovaj se izraz naziva harmonijskom sredinom brojeva a i b. Iz slike 5 očitavamo da je |ND| < |TD| < |OD| < |CD|, tj. sredine rastu ovim slijedom: harmonijska, geometrijska, aritmetička i kvadratna. Ova se činjenica generalizira na sredine definirane pomoću opće potencije, ali to prelazi okvire ovog rada.
Sljedeća dva dokaza pripadaju grupi tzv. analitičkih dokaza AG nejednakosti.
Dokaz 6.
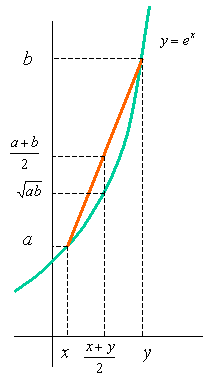
Funkcija f(x) = ex je konveksna, što geometrijski znači da je graf funkcije između dviju točaka na grafu uvijek ispod tetive koja spaja te dvije točke. Na grafu eksponencijalne funkcije odaberimo dvije točke s koordinatama (x,ex) i (y,ey) te uvedimo oznake a = ex i b = ey.
Pravac kroz odabrane točke ima jednadžbu
| Y − b = | b − a | (X − y), |
| y − x |
pa točka na tom pravcu s apscisom (x + y)/2 ima ordinatu (a + b)/2. S druge strane, točka s istom apscisom, ali na grafu eksponencijalne funkcije ima ordinatu e(x + y)/2, što nakon sređivanja postaje √ab. Budući da se točka na grafu nalazi ispod točke na tetivi, slijedi AG nejednakost
| √ab ≤ | a + b | . |
| 2 |
Dokaz 7.
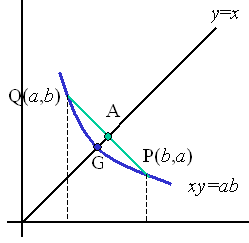
Promotrimo hiperbolu x·y = ab. Točke P(b,a) i Q(a,b) pripadaju toj hiperboli. Pravac koji prolazi kroz te dvije točke ima jednadžbu
Promotrimo sad presjek hiperbole i tetive PQ s pravcem y = x. Na hiperboli je presjek točka G s koordinatama
a na tetivi točka A s koordinatama
| A ( | a + b | , | a + b | ). |
| 2 | 2 |
Budući da je točka G ispod točke A (zbog konveksnosti funkcije čija je hiperbola graf), slijedi AG nejednakost.
AG nejednakost je snažno sredstvo za dokazivanje raznih složenijih nejednakosti i u literaturi se mogu naći brojni zadaci koji se svode na upotrebu ove nejednakosti. U sljedećih nekoliko primjera pokazat ćemo neke primjene opće AG nejednakosti.
Primjer 1: Maksimum polinoma.
Ako je L površina sferne kapice danog polumjera R i V volumen odgovarajućeg sfernog odsječka, tada vrijedi 18πV2 ≤ L3, pri čemu jednakost vrijedi ako i samo ako je riječ o polusferi.
Dokaz. Koristeći poznate formule za površinu sferne kapice L = 2πRh i volumen sfernog odsječka V = πh2(3R−h)/3 dobivamo omjer
| V2 | = | h (3R−h)2 | . |
| L3 | 72πR3 |
Nađimo maksimum polinoma h (3R−h)2 za h ∈ [0,R]. Napišimo AG nejednakost za tri broja C1h, C2(3R−h) i C2(3R−h), pri čemu su C1 i C2 neodređeni koeficijenti:
| C1h C22(3R−h)2 ≤ | ( | C1h + 2C2(3R−h) | ) | 3 | . |
| 3 |
Koeficijente C1 i C2 odredimo tako da u aritmetičkoj sredini na desnoj strani nejednakosti nestane varijabla h. Dobivena konstanta na desnoj strani bit će maksimum polinoma na lijevoj strani ako postoji h0 za koji se postiže jednakost.
Varijabla h nestat će ako vrijedi C1−2C2 = 0. Bez smanjenja općenitosti uzmimo da je C1 = 2 i C2 = 1. Jednakost u AG nejednakosti postiže se ako su brojevi jednaki, tj. ako vrijedi C1h = C2(3R−h), odakle dobivamo da je h0 = R. Uvrštavanjem koeficijenata C1 i C2 u AG nejednakost dobivamo 2h(3R−h)2 ≤ 8R3, tj. h(3R−h)2 ≤ 4R3. Dakle, vrijedi
| V2 | ≤ | 1 | . |
| L3 | 18π |
Jednakost se postiže ako i samo ako je visina kapice jednaka polumjeru (tj. kapica je u stvari polusfera).
Ova metoda s uvođenjem neodređenih koeficijenata i korištenjem AG nejednakosti može se generalizirati za opću situaciju određivanja maksimuma polinoma koji je dan u obliku produkta.
Primjer 2: Limes.
|
|
= 1. |
Dokaz. Pretpostavimo da je n ≥ 3. Tada koristeći AG nejednakost za n brojeva 1, n1/n, n2/n, …, n(n−1)/n imamo
| 0 ≤ n1/n − 1 = | n − 1 | ||||
| 1 + n1/n + … + n(n−1)/n | |||||
| ≤ | n − 1 | ||||
| n (n1/n + 2/n +…+(n−1)/n)1/n | |||||
| = | n − 1 | ≤ | 1 | . | |
| n(3n−1)/(2n) | n1/3 | ||||
Budući da n-1/3 teži k 0 kada n teži u beskonačnost, slijedi da tada i n1/n − 1 teži k 0.
Primjer 3: Hölderova nejednakost.
Neka su a i b dvije n-torke pozitivnih realnih brojeva te neka su p i q dva pozitivna broja takva da je 1/p + 1/q = 1. Tada vrijedi
| n | akbk ≤ | ( | n | akp | ) | 1/p | ( | n | bkq | ) | 1/q | . |
| ∑ | ∑ | ∑ | ||||||||||
| k=1 | k=1 | k=1 |
Dokaz. Gornja nejednakost može se napisati u obliku
| n | ( |
|
) | 1/p | ( |
|
) | 1/q | ≤ 1, | ||||
| ∑ | |||||||||||||
| k=1 |
a ta se nejednakost dokazuje koristeći težinsku AG nejednakost za dva broja:
| n | ( |
|
) | 1/p | ( |
|
) | 1/q | ≤ | ||||
| ∑ | |||||||||||||
| k=1 |
| ≤ | n | ( |
|
· |
|
+ |
|
· |
|
) | = | ||||||||
| ∑ | |||||||||||||||||||
| k=1 |
| = | 1 | + | 1 | = 1. |
| p | q |
1. Aritmetičko-geometrijska nejednakost
2. Dokazi AG nejednakosti
3. Primjene AG nejednakosti