
| Dokazi bez riječi, 64 = 65 i zlatni rez |  |  |
|
Sadržaj: 1. 64 = 65?Kako bi što zornije prikazali neku relaciju ili opravdali određeni postupak, nastavnici često u nastavi matematike posežu za takozvanim vizualnim dokazima, odnosno dokazima bez riječi. Školarcima je možda najpoznatiji takav dokaz Pitagorinog poučka (slika 1). 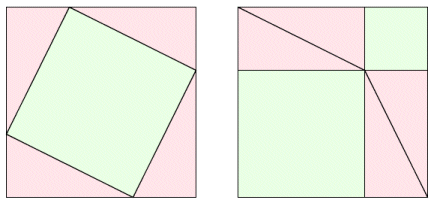
Slika 1. No, nekritička upotreba dokaza bez riječi krije zamke. Ponekad stvari nisu takve kao što izgledaju. Jedan od klasičnih primjera takve zamke je "dokaz" bez riječi tvrdnje 64 = 65. 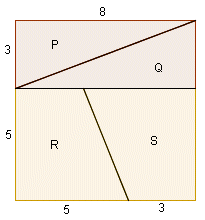
Slika 2. Radi se o kvadratu stranice duljine 8 razdijeljenom na četiri dijela: dva sukladna pravokutna trokuta s katetama 3 i 8 te dva sukladna pravokutna trapeza s osnovicama 3 i 5 i visinom 5 (slika 2). Od tih je dijelova sastavljen pravokutnik sa stranicama duljina 5 i 13 (slika 3). Površina kvadrata je 64, a površina pravokutnika 65. Na prvi pogled čini se da je 64 = 65. 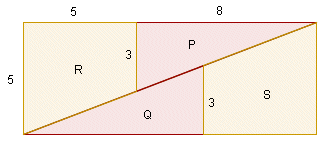
Slika 3. Gdje je greška? Označimo s d, b i m redom duljine hipotenuze pravokutnog trokuta P, kraka trapeza R i dijagonale pravokutnika na slici 3. Primjenom Pitagorinog poučka dobivamo d = √73 ≈ 8.5440, b = √29 ≈ 5.3852 i m = √194 ≈ 13.9284. Očito je √73 + √29 > √194, tj. hipotenuza trokuta P, krak trapeza R i dijagonala pravokutnika čine trokut. Odnosno, na slici 3 krije se paralelogram sa stranicama duljina √73 i √29, površine 1. Na slici 4 taj je paralelogram prikazan nešto uvećan. 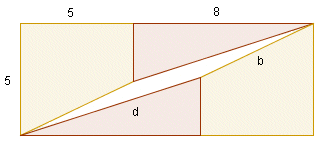
Slika 4. Napomena. Brojevi 5, 8 i 13 uzastopni su Fibonaccijevi brojevi. Njihov odnos 5·13 - 82 = 1 specijalni je slučaj Cassinijevog identiteta za Fibonaccijeve brojeve: Fn+1·Fn-1 - Fn2 = (-1)n. Više informacija o ovom identitetu i kako se pomoću njega generalizira "dokaz" da je 64 = 65, možete naći u knjizi A. Dujelle [DU]. 2. Zlatni rezAko dužinu AB podijelimo točkom C na dva dijela tako da je omjer duljina većeg dijela i cijele dužine jednak omjeru duljina manjeg i većeg dijela, kažemo da smo dužinu podijelili u omjeru zlatnog reza. 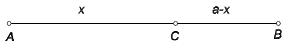
Slika 5. Označimo li duljinu dužine AB s a i duljinu dužine AC s x, dobivamo x : a = (a-x) : x, odakle je
Broj φ = (√5 - 1) / 2 naziva se omjerom zlatnog reza ili zlatnim brojem. Omjer zlatnog reza javlja se na raznim mjestima u matematici, umjetnosti, arhitekturi i drugdje. No, u kakvoj je on vezi s problemom opisanim u prethodnom poglavlju? Promotrimo pitanje jednakosastavljivosti kvadrata i pravokutnika: postoji li takva podjela stranice kvadrata da se dijelovi P, Q, R i S stvarno mogu presložiti u pravokutnik? Neka je stranica kvadrata podijeljena na dijelove duljina x i y, pri čemu je x < y, te neka je kvadrat podijeljen na dijelove P, Q, R i S kao na slici 6. 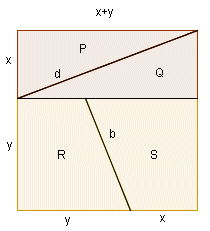
Slika 6. Prvi uvjet koji mora vrijediti da bi se ti dijelovi kvadrata mogli presložiti u pravokutnik kao na slici 7 jest jednakost površina kvadrata i pravokutnika: (x + y)2 = y·(x + 2y). Iz tog uvjeta dobivamo da je
tj. brojevi x i y u omjeru su zlatnog reza. 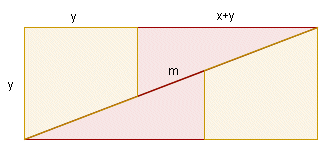
Slika 7. Dokažimo sada da ako su brojevi x i y u omjeru zlatnog reza, onda se pri preslaganju u pravokutnik ne pojavljuje paralelogram. Točnije, dokažimo da je d + b = m, pri čemu je d duljina hipotenuze trokuta P s katetama x i x + y, b je duljina kraka trapeza R, a m je duljina dijagonale pravokutnika sa stranicama y i x + 2y (slika 7). Pri dokazu ove tvrdnje koristimo se činjenicom da za zlatni broj φ vrijedi φ2 = 1 - φ. Koristeći se Pitagorinim poučkom dobivamo:
Pomoću ovih izraza lako se pokazuje da je d + b = m. Dakle, u slučaju kad je stranica kvadrata razdijeljena na dijelove kojima su duljine u omjeru zlatnog reza, preslaganjem kvadrata na opisani način dobiva se pravokutnik. To je jedini slučaj diobe stranice kvadrata kad se pojavljuje takva situacija. Napomena. Slike u ovom članku nacrtane su pomoću programa GeoGebra [HO]. Dostupni su "radni listovi" (worksheets) u kojima su definirane: slike.zip. Literatura
|
