
Broj 7















Dino Sejdinović i Alen Kopić
O Oberwolfach problemu


Sadržaj:
1. Uvod
2. Porijeklo naziva
3. Osnovni pojmovi teorije grafova
4. Klasični Oberwolfach problem
5. Varijanta problema s parovima
6. Opći slučaj
7. Uniformni problem
8. Neki rezultati za neuniformni problem
9. Dva jednostavna primjera
Literatura
1. Uvod
U ovom radu razmatrat ćemo jedan otvoreni problem teorije grafova, takozvani Oberwolfach problem. Formalno, radi se o problemu faktorizacije grafa G, koji je potpun graf s neparnim brojem vrhova ili graf koji se dobije iz potpunog grafa s parnim brojem vrhova uklanjanjem nekog njegovog 1-faktora. Treba ispitati da li je moguće faktorizirati G na međusobno izomorfne 2-faktore zadanog oblika. Ovdje ćemo također razmatrati varijacije i poopćenja ovog problema, navesti do sada ostvarene rezultate i dati primjere faktorizacije malih grafova G.
U manje teorijskoj formulaciji klasični Oberwolfach problem zapravo predstavlja problem rasporeda sjedenja neparnog broja osoba n za određenim brojem okruglih stolova u (n-1)/2 navrata, tako da svaka osoba pored svake od ostalih sjedi točno jednom. Na primjer, zamislite da organizirate znanstvenu konferenciju iz neke posve nove matematičke discipline, na kojoj sudjeluje 21 znanstvenik. Večere se održavaju u prostoriji u kojoj su tri okrugla stola s po sedam stolica svaki (drugu dvoranu zauzeli su fizičari). Ukupno će se održati deset konferencijskih večera. Kao organizatoru, glavni vam je cilj da se svaki od sudionika što bolje upozna sa svim ostalima. Nema bolje prilike za upoznavanje i razmjenu mišljenja od sjedenja jedan pored drugog tijekom večere! S obzirom da se održava deset večera, ispunjen je nuždan uvjet da svaka osoba sjedi točno jednom pored svake od ostalih. Svaku večer sjedit će pored dviju osoba (stolovi su okrugli!). Da li je uz te uvjete moguće napraviti odgovarajući raspored sjedenja?
Što ako se broj sudionika promijeni? Što ako nisu svi stolovi iste veličine? Na primjer, vlasnik hotela odlučio je fizičarima prepustiti dvoranu s trima velikim stolovima, a večere matematičara smjestiti u prostoriju u kojoj se nalaze četiri okrugla stola s po četiri stolice i jedan okrugli stol s pet stolica. Postoji li tada dobar raspored? Što ako svaki sudionik dolazi sa svojim supružnikom, također matematičarom ili matematičarkom? Ne morate brinuti o međusobnom upoznavanju bračnih parova, ali i dalje trebate svaku osobu upoznati sa svim ostalima (izuzev njezinog bračnog druga). Odgovore na ova i slična pitanja daje teorija Oberwolfach problema. U općenitoj formulaciji problem je otvoren i jako je malo rezultata koji govore o slučajima sa stolovima različite veličine. Također, algoritmi koji traže rješenja Oberwolfach problema dosta su ograničeni i uglavnom se svode na pretraživanje grubom silom ("brute force"). Do sada ne postoji opća metoda određivanja rasporeda sjedenja na konferencijskim večerama, već problem treba rješavati za svaku konferenciju posebno. Stoga bi od rješavanja ovog problema imala korist cjelokupna znanstvena zajednica, a naročito organizatori konferencija. Moglo bi se tada pristupiti rješavanju mnogo dubljeg i težeg problema, starog koliko i mi sami: što ćemo za večeru?
2. Porijeklo naziva
Oberwolfach problem prvi je formulirao Ringel 1967. godine [GU]. Problem je dobio ime po jednom od najprestižnijih matematičkih instituta u svijetu, Mathematisches Forschungsinstitut Oberwolfach, smještenom u mjestašcu Oberwolfach-Walke na živopisnim obroncima gorja Schwarzwald u Njemačkoj. U više od pola stoljeća postojanja ovaj institut bio je mjesto održavanja oko 3000 raznih konferencija i seminara na kojima su sudjelovali matematičari iz cijelog svijeta, među njima i imena kakva su A.M. Ostrowski, P. Erdös, J.-P. Serre, J.A.E. Dieudonné i drugi. Na ovim konferencijama u pravilu vlada neformalna atmosfera, koju možda inspirira živopisni krajolik u kojem je institut smješten. Među ostalim neobičnim ritualima, kojima je cilj da se sudionici konferencija što bolje upoznaju (na primjer, u sobama za posjetioce nema televizora, radija, telefona ni brava), postoji i ritual slučajnog odabira rasporeda sjedenja na samim konferencijama, kao i pri zajedničkim objedima. Više o Oberwolfach institutu možete pročitati u članku [JA].

Slika 1. Matematički institut u Oberwolfachu
3. Osnovni pojmovi teorije grafova
Oberwolfach problem zapravo je problem teorije grafova, matematičke discipline kojoj se nastanak veže za čuveni Eulerov problem Königsberških mostova i za problem četiriju boja. Za čitatelje koji nisu upućeni u terminologiju teorije grafova dat ćemo sažetu listu definicija koje u daljnjem tekstu koristimo.
Neusmjereni multigraf (u daljem tekstu multigraf) G je uređeni
par (V, E), gdje:
|
Neka su u,v V,
u
V,
u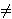 v. Ako je
e={u,v}
v. Ako je
e={u,v} E,
tada kažemo da su vrhovi u i v susjedni i da ih spaja brid e,
odnosno da su u i v krajevi brida e.
Ako E sadrži više od jednog primjerka neuređenog para {u,v}, tada
potfamiliju svih neuređenih parova {u,v} nazivamo višestrukim bridom.
Brid {u,u} naziva se petljom multigrafa G. Multigraf bez
višestrukih bridova i bez petlji naziva se jednostavnim grafom (u daljnjem tekstu
graf). U tom slučaju familija E je skup kojem su elementi dvočlani podskupovi
od V. Ako za E uzmemo familiju uređenih parova vrhova grafa G,
govorimo o usmjerenom grafu ili digrafu.
E,
tada kažemo da su vrhovi u i v susjedni i da ih spaja brid e,
odnosno da su u i v krajevi brida e.
Ako E sadrži više od jednog primjerka neuređenog para {u,v}, tada
potfamiliju svih neuređenih parova {u,v} nazivamo višestrukim bridom.
Brid {u,u} naziva se petljom multigrafa G. Multigraf bez
višestrukih bridova i bez petlji naziva se jednostavnim grafom (u daljnjem tekstu
graf). U tom slučaju familija E je skup kojem su elementi dvočlani podskupovi
od V. Ako za E uzmemo familiju uređenih parova vrhova grafa G,
govorimo o usmjerenom grafu ili digrafu.
Potpun graf Kn je jednostavan graf s n vrhova,
u kojem su svaka dva različita vrha susjedna. Potpun multigraf
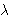 Kn je
multigraf s n vrhova, u kojem svaki par vrhova spaja
točno Kn je
multigraf s n vrhova, u kojem svaki par vrhova spaja
točno 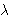 različitih bridova
multigrafa, tj. višestruki brid veličine različitih bridova
multigrafa, tj. višestruki brid veličine 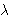 . .
|
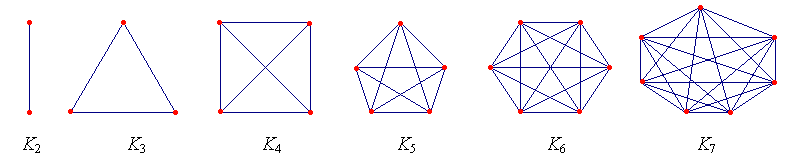
Slika 2. Primjeri potpunih grafova
Podgraf H grafa G, u oznaci H 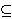 G, je graf sa skupom vrhova V(H)
G, je graf sa skupom vrhova V(H) 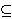 V(G) i familijom bridova
V(G) i familijom bridova
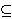 E(G).
E(G). V(G).
V(G).
Grafovi G1 i G2 su izomorfni, što se označava
G1  G2, ako postoji bijekcija G2, ako postoji bijekcija
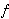 :V(G1) :V(G1)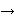 V(G2), takva da je {u,v} V(G2), takva da je {u,v}  E(G1) ako i samo ako
je { E(G1) ako i samo ako
je {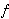 (u), (u),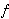 (v)} (v)}  E(G2).
Preslikavanje E(G2).
Preslikavanje 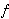 u tom slučaju nazivamo izomorfizmom grafova G1
i G2. u tom slučaju nazivamo izomorfizmom grafova G1
i G2.
|
Staza je konačan neprazan niz
W=v0e1v1e2v2...ekvk
u kojem se alternativno izmjenjuju vrhovi i bridovi grafa G, pri čemu su vrhovi
vi-1 i vi krajevi brida ei,
za svako 1 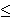 i
i 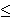 k,
i pritom su svi bridovi različiti. Put u grafu G je staza u kojoj su
svi vrhovi različiti. Ako su u putu W početni vrh v0 i
završni vrh vk jednaki, takav se put zove zatvorenim putem
ili ciklusom. Dva vrha u i v su povezana ako
između njih postoji put u G. Lako se pokazuje da je povezanost relacija
ekvivalencije na skupu vrhova V(G). Klase ekvivalencije nazivamo komponentama
povezanosti grafa G. Graf je povezan ako ima točno jednu komponentu
povezanosti.
k,
i pritom su svi bridovi različiti. Put u grafu G je staza u kojoj su
svi vrhovi različiti. Ako su u putu W početni vrh v0 i
završni vrh vk jednaki, takav se put zove zatvorenim putem
ili ciklusom. Dva vrha u i v su povezana ako
između njih postoji put u G. Lako se pokazuje da je povezanost relacija
ekvivalencije na skupu vrhova V(G). Klase ekvivalencije nazivamo komponentama
povezanosti grafa G. Graf je povezan ako ima točno jednu komponentu
povezanosti.
| Neka je {E1, E2,...,Et} particija familije E(G) bridova grafa G na disjunktne potfamilije. Ako je Hi = G[Ei], tada kažemo da je {H1, H2,...,Ht} dekompozicija grafa G na podgrafove H1, H2,...,Ht. |
4. Klasični Oberwolfach problem
Klasični (Ringelov) Oberwolfach problem glasi: "Neka na nekoj konferenciji
imamo neparan broj sudionika n. Da li je moguće da tih n sudionika
sjedi za s okruglih stolova T1,
T2,...,Ts, gdje za stol Ti
treba smjestiti ti  3 osoba, pri čemu je
3 osoba, pri čemu je 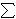 i ti = n,
tako da u (n-1)/2 navrata svaka osoba sjedi pored svake od ostalih
točno jednom?". Uvest ćemo još jednu definiciju kako bismo problem mogli lakše formulirati
na jeziku teorije grafova.
i ti = n,
tako da u (n-1)/2 navrata svaka osoba sjedi pored svake od ostalih
točno jednom?". Uvest ćemo još jednu definiciju kako bismo problem mogli lakše formulirati
na jeziku teorije grafova.
|
Specijalno, 2-faktor grafa G je graf H = (V(G),
F), gdje je F 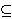 E(G) i svaki vrh iz G incidentan je s točno
dva brida u F. Primijetimo da je svaka komponenta povezanosti proizvoljnog 2-faktora
grafa G ciklus dužine d
E(G) i svaki vrh iz G incidentan je s točno
dva brida u F. Primijetimo da je svaka komponenta povezanosti proizvoljnog 2-faktora
grafa G ciklus dužine d  3 u G, kao povezan 2-regularan graf.
3 u G, kao povezan 2-regularan graf.
Sada Oberwolfach problem možemo formulirati ovako: "Neka je n neparan broj. Postoji li 2-faktorizacija potpunog grafa Kn u kojoj se svaki 2-faktor sastoji od ciklusa dužina t1, t2,...,ts, gdje su t1, t2,...,ts unaprijed zadani?".
Primjer 4.1. Neka na konferenciji sudjeluje 7 znanstvenika koji na raspolaganju imaju prostoriju s dvama stolovima. Za jednim stolom su tri stolice, a za drugim četiri. Označimo znanstvenike brojevima od 1 do 7, a stolove s I i II. Potrebno je organizirati raspored sjedenja u 3 navrata tako da svaki znanstvenik sjedi pored svakog od ostalih točno jednom. Dakle, govorimo o klasičnom problemu s n = 7, s = 2, t1 = 3 i t2 = 4. Ovakav je raspored moguć i možemo ga opisati na sljedeći način. Smatramo da je dani raspored sjedenja ciklički, tj. prvi i posljednji znanstvenik sjede jedan kraj drugog.
| Stol I | Stol II | |
| Večera 1 | 1, 2, 3 | 4, 5, 6, 7 |
| Večera 2 | 1, 4, 6 | 2, 5, 3, 7 |
| Večera 3 | 1, 5, 7 | 2, 6, 3, 4 |
5. Varijanta problema s parovima
Često se razmatra i sljedeća varijanta Oberwolfach problema, u kojoj imamo graf s
parnim brojem vrhova. U radu iz 1979. godine formulirali su je Huang, Kotzig
i Rosa [HK]: "Na konferenciji se nalazi m
parova. Da li je moguće sastaviti raspored sjedenja za s okruglih
stolova T1, T2,...,Ts,
gdje za stol Ti treba smjestiti
ti  3 osoba, pri čemu je
3 osoba, pri čemu je 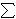 i ti = 2m,
tako da u m–1 navrata svaka osoba sjedi do svake od ostalih osoba,
izuzev svog supružnika, točno jednom?". S obzirom na ograničenje da nijedna osoba
ne sjedi kraj svojeg supružnika, jasno je da u ovom problemu nemamo potpun graf.
Naime, iz potpunog grafa potrebno je ukloniti određeni broj bridova tako da svaki vrh
bude incidentan s točno jednim od njih. Treba izvršiti sparivanje vrhova - naznačiti
koji parovi vrhova predstavljaju supružnike. Drugim riječima, potrebno je ukloniti
jedan 1-faktor potpunog grafa. To nam daje povod za sljedeću definiciju:
i ti = 2m,
tako da u m–1 navrata svaka osoba sjedi do svake od ostalih osoba,
izuzev svog supružnika, točno jednom?". S obzirom na ograničenje da nijedna osoba
ne sjedi kraj svojeg supružnika, jasno je da u ovom problemu nemamo potpun graf.
Naime, iz potpunog grafa potrebno je ukloniti određeni broj bridova tako da svaki vrh
bude incidentan s točno jednim od njih. Treba izvršiti sparivanje vrhova - naznačiti
koji parovi vrhova predstavljaju supružnike. Drugim riječima, potrebno je ukloniti
jedan 1-faktor potpunog grafa. To nam daje povod za sljedeću definiciju:
| Ako je n paran broj, onda s Kn – I označavamo graf nastao iz potpunog grafa Kn uklanjanjem bridova jednog 1-faktora. |
Graf Kn – I definiran je jednoznačno do izomorfizma. Primijetimo da, s obzirom da je 1-faktor pokrivajući graf u kojem su svaka dva brida nesusjedna, on sadrži točno m = n/2 bridova. Razapinjući 1-faktor naziva se još i savršenim sparivanjem grafa G. Sad Oberwolfach problem za paran broj osoba na jeziku teorije grafova glasi: "Neka je n paran broj. Postoji li 2-faktorizacija grafa Kn – I u kojoj se svaki 2-faktor sastoji od ciklusa dužina t1, t2,...,ts, gdje su t1, t2,...,ts unaprijed zadani?".
Primjer 5.1. Neka na konferenciji sudjeluju tri bračna para i neka na raspolaganju imaju prostoriju s jednim stolom za kojim je šest stolica. Treba napraviti raspored sjedenja u dva navrata tako da svatko sjedi točno jednom pored svakog drugog, izuzev svojeg supružnika. Dakle, radi se o varijanti Oberwolfach problema s parovima za n = 6, s = 1 i t1 = 6. Označimo znanstvenike s A1, B1, A2, B2, A3, B3, pri čemu bračni par čine Ai i Bi, i=1,2,3. Raspored je moguć i opisan je u sljedećoj tablici. Kao i u primjeru 4.1, prvu i posljednju osobu smatramo susjednim.| Stol I | |
| Večera 1 | A1, A2, A3, B1, B3, B2 |
| Večera 2 | A1, A3, B2, B1, A2, B3 |
6. Opći slučaj
Sada razmotrimo opći slučaj. U najopćenitijem obliku, neorijentirani Oberwolfach
problem je pitanje možemo li, ako su dani multigrafovi G,
H1, H2,...,Hm,
particionirati G na m faktora G1,
G2,...,Gm, takvih da je Gi
izomorfan s Hi, za i  {1,2,...,n}. Ovaj problem označavamo
OP(G; H1, H2,...,Hm).
Ako su svi multigrafovi Hi izomorfni nekom multigrafu H,
takav problem označavamo OP(G; H). Za dane G i H, broj m
takav da se G dekomponira na m faktora izomorfnih s H, ako postoji,
jednoznačno je određen – dan je s |E(G)| / |E(H)|. Zato ga u oznaci
nije potrebno navoditi. Ako su G i H jednostavni grafovi i ako
su komponente povezanosti grafa H ciklusi, i to njih n1 duljine
a1, n2 duljine a2, ...,
nk duljine ak, tada problem označavamo
OP(G; a1n1,
a2n2,...,aknk).
Ako je G = Kn za neparni n ili
G = Kn – I za parni n, u oznaci se obično
izostavlja G. Tada imamo klasični Oberwolfach problem, odnosno varijantu
Huang–Kotzig–Rosa.
{1,2,...,n}. Ovaj problem označavamo
OP(G; H1, H2,...,Hm).
Ako su svi multigrafovi Hi izomorfni nekom multigrafu H,
takav problem označavamo OP(G; H). Za dane G i H, broj m
takav da se G dekomponira na m faktora izomorfnih s H, ako postoji,
jednoznačno je određen – dan je s |E(G)| / |E(H)|. Zato ga u oznaci
nije potrebno navoditi. Ako su G i H jednostavni grafovi i ako
su komponente povezanosti grafa H ciklusi, i to njih n1 duljine
a1, n2 duljine a2, ...,
nk duljine ak, tada problem označavamo
OP(G; a1n1,
a2n2,...,aknk).
Ako je G = Kn za neparni n ili
G = Kn – I za parni n, u oznaci se obično
izostavlja G. Tada imamo klasični Oberwolfach problem, odnosno varijantu
Huang–Kotzig–Rosa.
| Oblik 2-faktora F je multiskup {a1n1, a2n2,...,aknk}, gdje su ai međusobno različite duljine ciklusa u F, a ni broj ciklusa duljine ai. |
Sada Oberwolfach problem OP(a1n1,
a2n2,...,aknk)
glasi: mogu li se bridovi od Kn ili
Kn – I, za n = 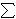 i niai,
podijeliti na izomorfne 2-faktore zadanog oblika?
i niai,
podijeliti na izomorfne 2-faktore zadanog oblika?
7. Uniformni problem
Problem OP(am), u kojem svi ciklusi imaju istu duljinu, zovemo uniformnim Oberwolfach problemom. Problem OP(a), tj. uniformni problem za m=1, nije ništa drugo nego dekompozicija potpunog grafa Kn ili grafa Kn – I u Hamiltonove cikluse. U formulaciji problema kao rasporeda sjedenja na konferencijskim večerama uniformnost znači da svi stolovi imaju jednak broj stolica.
Rješenje uniformnog Oberwolfach problema daje sljedeći teorem, koji je rezultat Alspacha, Schellenberga, Stinsona i Wagnera [AS].
Teorem 7.1. Za n  3 problem OP(am) ima rješenje kad
god je a
3 problem OP(am) ima rješenje kad
god je a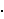 m = n,
osim što OP(32) i OP(34) nemaju rješenje.
m = n,
osim što OP(32) i OP(34) nemaju rješenje.
Uvjet a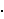 m = n
očito je nuždan za egzistenciju rješenja. Dakle, teorem tvrdi da rješenje uvijek postoji ako
je zadovoljen nužni uvjet, osim u dvama navedenim slučajima. Ilustrirajmo zašto OP(32)
nema rješenje. Ako na prvom od sastanaka tri para osoba sjede za dva stola i za svakim
od stolova su tri stolice, tada npr. osoba A sjedi do osoba B i C. Na idućem sastanku, nijedna
od osoba B i C ne smije sjediti za istim stolom za kojim sjedi osoba A. No, to bi značilo
da osobe B i C sjede za istim stolom pa sjede jedna pored druge! Dakle, na drugom sastanku
sigurno bi se ponovio jedan par susjeda pa je traženi raspored sjedenja nemoguć. Slično bi
se pokazalo i da OP(34) nema rješenje.
m = n
očito je nuždan za egzistenciju rješenja. Dakle, teorem tvrdi da rješenje uvijek postoji ako
je zadovoljen nužni uvjet, osim u dvama navedenim slučajima. Ilustrirajmo zašto OP(32)
nema rješenje. Ako na prvom od sastanaka tri para osoba sjede za dva stola i za svakim
od stolova su tri stolice, tada npr. osoba A sjedi do osoba B i C. Na idućem sastanku, nijedna
od osoba B i C ne smije sjediti za istim stolom za kojim sjedi osoba A. No, to bi značilo
da osobe B i C sjede za istim stolom pa sjede jedna pored druge! Dakle, na drugom sastanku
sigurno bi se ponovio jedan par susjeda pa je traženi raspored sjedenja nemoguć. Slično bi
se pokazalo i da OP(34) nema rješenje.
Teorem 7.1 može se proširiti na uniformni Oberwolfach problem za potpune multigrafove, o čemu govori sljedeći teorem (Gvozdjak [GV]).
Teorem 7.2. Neka je 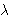
 1
i G =
1
i G = 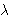 Kn ako je n neparan
ili
Kn ako je n neparan
ili 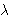 paran, odnosno
G =
paran, odnosno
G = 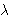 Kn - I
ako je n paran i
Kn - I
ako je n paran i 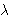 neparan. Neka su dalje a
neparan. Neka su dalje a  3
i m
3
i m  1 takvi da je
a
1 takvi da je
a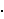 m = n.
Tada OP(G; am) ima rješenje ako i samo ako nije ispunjen
nijedan od sljedećih uvjeta:
m = n.
Tada OP(G; am) ima rješenje ako i samo ako nije ispunjen
nijedan od sljedećih uvjeta:
-
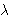
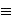 2 (mod 4), a = 3, m = 4,
2 (mod 4), a = 3, m = 4, -
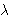 je neparan, a = 3,
m = 2,
je neparan, a = 3,
m = 2, -
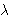 = 1, a = 3, m = 4.
= 1, a = 3, m = 4.
Oberwolfach problem za potpun multigraf 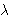 Kn tumačimo kao rasporede sjedenja na
konferenciji s neparnim brojem sudionika n, na kojoj će svaki od
sudionika u tijeku
Kn tumačimo kao rasporede sjedenja na
konferenciji s neparnim brojem sudionika n, na kojoj će svaki od
sudionika u tijeku 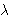 (n-1)/2 sastanaka sjediti pored svakog drugog
točno
(n-1)/2 sastanaka sjediti pored svakog drugog
točno 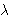 puta.
Dakle, radi se o
puta.
Dakle, radi se o 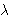 -tematskoj
konferenciji.
-tematskoj
konferenciji.
8. Neki rezultati za neuniformni problem
Zahvaljujući navedenim teoremima, uniformni Oberwolfach problem u potpunosti je riješen. No, za općeniti, neuniformni problem rješenje je poznato samo u malom broju specijalnih slučaja. U sljedećem teoremu navodimo neke do sada poznate rezultate.
Teorem 8.1. Sljedeći Oberwolfach problemi imaju rješenje:
- OP(3, a) za sve neparne a
 5,
5, - OP(4, a) za sve parne a
 4,
4, - OP(a, a + 2) za sve a
 3,
3, - OP(a, a + 1) za sve a
 3,
a
3,
a  4,
4, - OP(3, 8a - 2) za sve a
 1,
1, - OP(3, (4a)2) za sve a
 1,
1, - OP((2a + 1)2, 2a + 2) za sve a
 1,
1, - OP(a2, 2
 a/2
a/2![]](../symbols/rceil.gif) + 2c)
za sve a
+ 2c)
za sve a  3 i svaki c = 0, 2, 3,...,
3 i svaki c = 0, 2, 3,..., - OP(2a + 1, 4r) za sve a
 1 i r
1 i r  1,
1, - OP(2a + 1, (4a)r) za sve a
 1 i r
1 i r  1,
1, - OP(a1r, a2) za sve
r
 1,
a1
1,
a1  3,
a2
3,
a2  4a1r - 1.
4a1r - 1.
Svi navedeni rezultati tiču se slučaja s dvjema različitim vrstama ciklusa, tj. problema oblika OP(an, bm). Dalje, osim u tvrdnjama 8 i 11, imamo ovisnost veličine ciklusa samo o jednom parametru, ili je jedna od veličina ciklusa konstanta.
Najveće pomake u slučaju kad veličine ciklusa ovise o dvama parametrima dao je
Gvozdjak [GV]. On je 2003. dokazao da OP(a, b)
ima rješenje za sve različite neparne a i b. Jako je malo rezultata
u slučaju triju različitih veličina ciklusa i gotovo se svi tiču problema OP(3,a,b).
Najprije je pokazano da  0 (mod 4).
0 (mod 4).
9. Dva jednostavna primjera
Sad ćemo detaljnije proučiti probleme iz primjera 4.1 i primjera 5.1. Primjer klasičnog Oberwolfach problema za graf K7, odnosno problem konferencije sa 7 osoba, razmatrao je Colbourn 1982. godine [CO]. Graf K7 ima dvije različite vrste 2-faktora: faktor A oblika {3,4} i faktor B oblika {7}. Postoje četiri moguća načina 2-faktorizacije grafa K7: to su AAA, AAB, ABB i BBB. Faktorizacije AAB i ABB nas ovdje ne zanimaju jer u njima nisu svi 2-faktori izomorfni. S druge strane, AAA i BBB, ako postoje, redom su rješenja problema OP(3,4) i OP(7). Egzistenciju rješenja problema OP(3,4) garantira tvrdnja 4 teorema 8.1, a OP(7) je uniformni problem za koji egzistenciju rješenja garantira teorem 7.1. Na narednim slikama predstavljeni su 2-faktori koji dekomponiraju K7 za probleme OP(3,4) i OP(7). Svaki od 2-faktora označen je posebnom bojom.
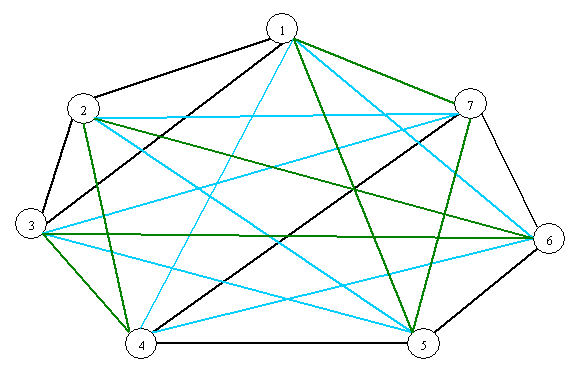
Slika 3. Faktorizacija grafa K7 na 2-faktore oblika {3,4}
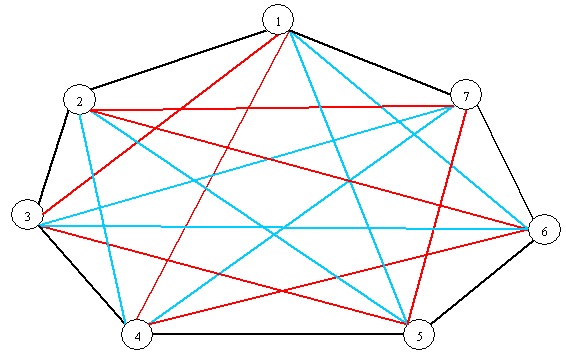
Slika 4. Faktorizacija grafa K7 na 2-faktore oblika {7}
Za konferenciju na kojoj sudjeluje tri para znanstvenika promatramo graf K6 - I, gdje je I jedan 1-faktor potpunog grafa K6. Moguće su dvije vrste 2-faktora, oblika {32} i {6}. Kao što smo prije vidjeli, OP(32) nema rješenja. Jedno rješenje uniformnog problema OP(6) vidimo na slici 5. Za razliku od ranije razmatranog rješenja, ovdje su znanstvenici označeni brojevima od 1 do 6, a 1-faktor koji se briše označen je isprekidanom linijom. To znači da su tri bračna para {1,4}, {2,6} i {3,5}.
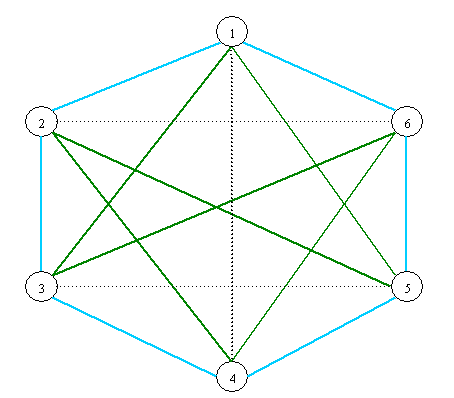
Slika 5. Faktorizacija grafa K6 - I na 2-faktore oblika {6}
Literatura
[AS] B. Alspach, P.J. Schellenberg, D.R. Stinson, D. Wagner, The Oberwolfach problem and factors of uniform odd length cycles. Journal of Combinatorial Theory, Series A 52 (1989), 20-43.
[BE] C. Berge, Graphes et hypergraphes. Dunod, Paris, 1970.
[CO] C.J. Colbourn, Hamiltonian decompositions of complete graphs. Ars Combinatoria 14 (1982), 261-269.
[FR] F. Franek, A. Rosa, Two-factorizations of small complete graphs. Journal of Statistical Planning and Inference, 86 (2000), 435-442.
[FS] D. Froncek, B. Stevens, Pancomponented 2-factorizations of complete graphs. Discrete Mathematics 299 (2005), 99-112.
[GU] R.K. Guy, Unsolved combinatorial problems. Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), str. 121-127. Academic Press, London, 1971.
[GV] P. Gvozdjak, On the Oberwolfach problem for cycles with multiple lengths. Disertacija, Simon Fraser University, 2003.
[HK] C. Huang, A. Kotzig, A. Rosa, On a variation of the Oberwolfach problem. Discrete Mathematics 27 (1979), 261-277.
[JA] A. Jackson, Oberwolfach, yesterday and today. Notices of the American Mathematical Society 47 (2000), 758-765.
[LL]
J. Liu, D.R. Lick, On 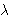 -fold
equipartite Oberwolfach problem with uniform table sizes. Annals of Combinatorics
7 (2003), 315-323.
-fold
equipartite Oberwolfach problem with uniform table sizes. Annals of Combinatorics
7 (2003), 315-323.
1. Uvod
2. Porijeklo naziva
3. Osnovni pojmovi teorije grafova
4. Klasični Oberwolfach problem
5. Varijanta problema s parovima
6. Opći slučaj
7. Uniformni problem
8. Neki rezultati za neuniformni problem
9. Dva jednostavna primjera
Literatura