


14. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Omišalj, 4. - 7. svibnja 2005.
Zadaci za VIII. razred
- Odredi sve troznamenkaste brojeve
abc
koji imaju svojstvo da je
22 / (a2 + b2 + c2) prirodan broj. - Nad stranicama pravokutnog trokuta konstruirani su
izvana jednakostranični trokuti. Za njih vrijedi da je zbroj
površina trokuta nad hipotenuzom i trokuta nad kraćom katetom
jednak zbroju površina trokuta nad duljom katetom i
pravokutnog trokuta. Izračunaj omjer duljina hipotenuze i
kraće katete.
- Nađi sve prirodne brojeve n za koje su ispravne točno
dvije od sljedeće tri tvrdnje:
1) Broj n je kvadrat prirodnog broja.
2) Posljednja znamenka broja n je 3.
3) Broj n + 15 je kvadrat prirodnog broja. - Ako za realni broj x, x > 1, vrijedi jednakost
koliko je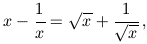
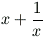 ?
?
- Neka je dana kružnica k središta S i promjera AB. U nju je upisana kružnica k1 tako da dira promjer AB u središtu S i kružnicu k. Kružnica k2 dira obje kružnice k i k1 te promjer AB. Dokaži da su središta tih triju kružnica vrhovi jednakokračnog trokuta.
