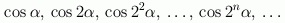13. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Trogir, 5. - 8. svibnja 2004.
Zadaci za IV. razred
- Neka je n prirodan broj i neka su
z1, ... ,
zn,
w1, ... ,
wn
kompleksni brojevi takvi da za svaki izbor brojeva
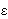 1, ... ,
1, ... ,
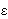 n
iz skupa {-1, 1} vrijedi
n
iz skupa {-1, 1} vrijedi
|
Dokažite da je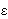 1z1 + ... +
1z1 + ... +
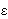 nzn|
nzn|
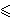 |
|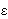 1w1 + ... +
1w1 + ... +
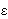 nwn|.
nwn|.
|z1|2 + ... + |zn|2
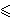 |w1|2 + ... +
|wn|2.
|w1|2 + ... +
|wn|2.
- Unutar trokuta ABC s duljinama stranica a, b,
c i odgovarajućim kutovima
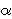 ,
,
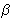 ,
,
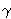 postoje točke P i Q takve da vrijedi
postoje točke P i Q takve da vrijedi
Dokažite da vrijedi jednakost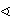 BPC =
BPC =
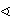 CPA =
CPA =
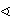 APB =
120o,
APB =
120o,
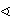 BQC =
60o +
BQC =
60o +
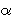 ,
,
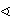 CQA =
60o +
CQA =
60o +
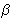 ,
,
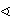 AQB =
60o +
AQB =
60o +
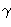 .
.
(|AP| + |BP| + |CP|)3
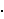 |AQ|
|AQ| 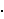 |BQ|
|BQ| 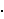 |CQ|
= (abc)2.
|CQ|
= (abc)2.
- Nizovi realnih brojeva
(xn),
(yn),
(zn),
n

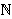 ,
definirani su formulama
,
definirani su formulama
xn +1 = 2xn / (xn2 - 1), yn +1 = 2yn / (yn2 - 1), zn +1 = 2zn / (zn2 - 1),
a početni članovi su x1 = 2, y1 = 4 i z1 takav da vrijedix1 y1 z1 =x1 + y1 + z1 .
a) Provjerite da su za svaki n
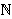 zadovoljeni uvjeti:
xn2
zadovoljeni uvjeti:
xn2
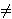 1,
yn2
1,
yn2
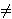 1,
zn2
1,
zn2
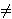 1.
1.
b) Da li postoji k
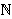 takav da je
xk +
yk +
zk = 0?
takav da je
xk +
yk +
zk = 0?
- Odredite sve realne brojeve
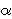 sa svojstvom da su svi brojevi u nizu
sa svojstvom da su svi brojevi u nizu
negativni.