Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
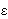 1, ... ,
1, ... ,
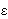 n
iz skupa {-1, 1} vrijedi
n
iz skupa {-1, 1} vrijedi
|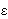 1z1 + ... +
1z1 + ... +
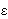 nzn|
nzn|
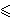 |
|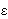 1w1 + ... +
1w1 + ... +
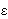 nwn|.
nwn|.
|z1|2 + ... +
|zn|2
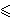 |w1|2 + ... +
|wn|2.
|w1|2 + ... +
|wn|2.
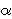 ,
,
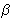 ,
,
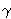 postoje točke P i Q takve da vrijedi
postoje točke P i Q takve da vrijedi
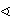 BPC =
BPC =
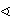 CPA =
CPA =
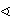 APB =
120o,
APB =
120o,
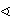 BQC =
60o +
BQC =
60o +
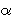 ,
,
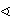 CQA =
60o +
CQA =
60o +
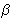 ,
,
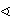 AQB =
60o +
AQB =
60o +
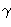 .
.
(|AP| + |BP| + |CP|)3
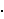 |AQ|
|AQ| 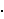 |BQ|
|BQ| 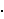 |CQ|
= (abc)2.
|CQ|
= (abc)2.

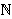 ,
definirani su formulama
,
definirani su formulama
xn +1 = 2xn / (xn2 - 1), yn +1 = 2yn / (yn2 - 1), zn +1 = 2zn / (zn2 - 1),
a početni članovi su x1 = 2, y1 = 4 i z1 takav da vrijedi
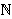 zadovoljeni uvjeti:
xn2
zadovoljeni uvjeti:
xn2
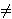 1,
yn2
1,
yn2
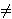 1,
zn2
1,
zn2
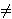 1.
1. 
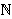 takav da je
xk +
yk +
zk = 0?
takav da je
xk +
yk +
zk = 0?
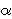 sa svojstvom da su svi brojevi u nizu
sa svojstvom da su svi brojevi u nizu