


11. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Zadar, 2. - 5. svibnja 2002.
Zadaci za VII. razred
- U kutiji se nalazi jednaki broj crvenih i plavih kuglica. Da smo u
kutiju stavili 3 crvene i 1 plavu kuglicu više, omjer broja crvenih
kuglica i ukupnog broja kuglica u kutiji bio bi veći od 0.503.
Koliki je najveći mogući broj crvenih kuglica u kutiji? - U svakom od dva voćnjaka uzgajaju se jabuke i kruške.
Pri tome stabla jabuke čine 65% broja stabala u prvom voćnjaku i 45%
broja stabala u drugom voćnjaku, odnosno 53% ukupnog broja stabala u
oba voćnjaka zajedno.
Koliki postotak ukupnog broja stabala u oba voćnjaka zajedno čine stabla iz prvog voćnjaka? - Odredi sve cijele brojeve a takve da je površina trokuta
što ga u koordinatnom sustavu određuju pravci
y = ax, y = 0 i
x + 2y - 4 = 0 prirodni broj.
- Dan je jednakostranični trokut ABC. Na stranici
AB odabrane su
točke M i N takve da je |AM| = |MN| = |NB|, a na stranici
AC točka P takva da je
|CP| = |AM|. Odredi
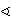 PMC +
PMC +
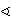 PNC.
PNC.
- Dan je trokut ABC površine 60 cm2. Neka su točka M na stranici AB i točka N na stranici BC takve da je |AM| = 2|MB| i |BN| = |NC|, te neka je točka P sjecište dužina AN i CM. Izračunaj površinu četverokuta MBNP.
