


5. MEDITERANSKO MATEMATIČKO NATJECANJE
Zagreb, 20. i 21. travnja 2002.
Zadaci
- Odredite sve prirodne brojeve x, y takve da
y | x2+1 i x2 | y3+1.
- Neka su x, y, a realni brojevi takvi da je
x + y = x3 + y3 = x5 + y5 = a.
Odredite sve moguće vrijednosti broja a. - Dan je šiljastokutan trokut ABC. Neka su M i N unutarnje
točke stranica AC i
BC, a K
polovište dužine MN.
Kružnice opisane trokutima CAN i BCM sijeku se (osim u točki C)
u točki D.
Dokažite da pravac CD prolazi kroz središte O opisane kružnice trokuta ABC ako i samo ako simetrala stranice AB prolazi kroz K. - Ako su a, b, c
nenegativni realni brojevi takvi da je
a2 + b2 +
c2 = 1, dokažite nejednakost
a / (b2+1) + b / (c2+1) + c / (a2+1)
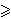 3/4 (a
3/4 (a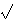 a +
b
a +
b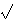 b +
c
b +
c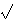 c)2.
c)2.
