
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
y | x2+1 i x2 | y3+1.
x + y = x3 + y3 = x5 + y5 = a.
Odredite sve moguće vrijednosti broja a.
a / (b2+1) + b / (c2+1) + c / (a2+1)
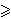 3/4 (a
3/4 (a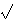 a +
b
a +
b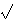 b +
c
b +
c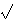 c)2.
c)2.