Sadržaj:

1. Uvod
2. P, NP i NP-potpuni problemi
3. SAT, logički sklopovi i dvije bitne činjenice
4. Što je Minesweeper problem?
5. Zašto je Minesweeper problem NP-potpun?
6. Zaključak
Literatura

1. Uvod

Tema ovog članka jest objašnjenje kako je igrica Minesweeper poslužila kao zanimljiv primjer u teoriji računarstva, točnije teoriji složenosti. Što je Minesweeper problem, kakve veze to ima s jednim od najvećih problema u matematici i računarstvu te kako se u cijelu priču uklapa svota od milijun dolara, neka su od pitanja na koja dajemo odgovor.

Računalna igrica Minesweeper nalazi se u svakom Windows operacijskom sustavu još od 1992. godine i većini čitatelja vjerojatno je dobro poznata. Možete je igrati on-line na adresi http://www.gameswizard.com/j_jvmine.html.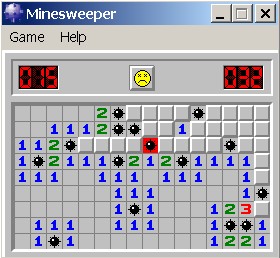

Slika 1.

Na početku igre dana je pravokutna tablica određene dimenzije. Iza svakog polja tablice može se nalaziti mina, a cilj igre je otkriti sve postavljene mine i pri tome, naravno, ne "nagaziti" na minirano polje već ga prikladno označiti. Dakle, igrač odabire i otkriva polje. Ako je polje minirano, tj. na njemu se nalazi mina, igrač gubi i igra staje. U suprotnom, igra se dalje nastavlja. Otvoreno polje iza kojeg nije mina sadrži broj od 0 do 8 koji predstavlja ukupan broj mina u osam susjednih kvadratića. Npr., moguće stanje tablice tijekom igre prikazuje slika:

Slika 2.

Polja označena brojevima su već otkrivena, dok ostala nisu. Dva polja koja sadrže * su već prepoznata kao minirana pa su tako označena. Ostala polja označena slovima u pravilu su neoznačena, jer o njima još ništa ne znamo, no tako smo ih označili radi lakšeg objašnjavanja. Dakako, cilj je otkriti preostale mine na tablici i označiti ih *. Prvo, polja A su minirana jer na to upućuju dva broja 2 "ispod". Polja označena slovom B su također minirana, zbog dvije četvorke i jedne petice "lijevo" od njih (primijetite da brojevi 4 i 5 prebrojavaju i već označene mine *). Analogno, C je minirano, no budući da su polja A, B, C minirana, zaključujemo da D i E ne sadrže mine. Možemo ih slobodno otvoriti te, u ovisnosti o brojevima koje kriju, odlučiti je li F miniran ili ne. Danu situaciju rješavali smo na ploči 6×6, no igra se može igrati na pločama raznih dimenzija, pri čemu pravila ostaju ista.

2. P, NP i NP-potpuni problemi

Nije rijetkost da su poneki algoritmi za rješavanje zadanog problema u praksi gotovo beskorisni. Naime, osim što je bitno znati kako riješiti problem, tj. imati sami algoritam, od velike važnosti je i to koliko je naš algoritam učinkovit. Svakom algoritmu potrebno je određeno vrijeme i memorijski prostor za izvršavanje, a svakako da nam je u cilju imati one što brže sa što manjom potrošnjom memorije. Ovdje na vrijeme gledamo kao na broj operacija koje algoritam mora izvršiti i izražavamo u ovisnosti o n, gdje je n neka mjera za veličinu skupa ulaznih podataka. Algoritam smatramo učinkovitim ako je vrijeme koje troši pri izvršavanju polinomno s obzirom na n (tj. ako mu je potrebno najviše C·n^k koraka, gdje je C konstanta te k prirodan broj).

Tako primjerice određivanje najvećeg zajedničkog djelitelja (Euklidov algoritam), množenje matrica te invertiranje regularnih matrica (Gaussove eliminacije) spada u klasu P.

S druge strane, postoje problemi za koje ne znamo spadaju li u klasu P. Jedan od takvih je i sljedeći primjer. Pretpostavimo da ste naslijedili veliko bogatstvo od daljeg rođaka. Sretni ste jer ćete konačno moći vratiti dugove prijateljima, skinuti hipoteku s kuće i napokon izaći iz minusa na bankovnom računu. Dakle, riječ je o velikom iznosu novca koji trebate vratiti. No, naslijeđeno bogatstvo je nekoliko vreća zlatnika. Svaki zlatnik je drukčije težine, pa stoga nemaju svi istu novčanu vrijednost (dapače, ne postoje dva iste težine). Iako znate kako imate dovoljno za vraćanje astronomsko velikog duga, ipak ga ne želite preplatiti, a niti ponovno ostati dužni prijateljima i banci, stoga morate sve vratiti točno u lipu! Postavlja se pitanje: možete li naći zlatnike čija će novčana vrijednost u zbroju odgovarati iznosu duga? Premda se ne zna za algoritam koji bi riješio opisani problem, a čije vrijeme izvršavanja polinomno ovisi u odnosu na iznos duga, ipak se može u polinomnom vremenu utvrditi je li neko ponuđeno rješenje za dani problem dobro. Naime, vrlo je jednostavno i lako zbrojiti vrijednosti nekog odabranog skupa zlatnika i vidjeti je li to traženi iznos, no teško je doći do pravog odabira.

Slična situacija je i s problemom SAT (eng. The satisfiability problem). Pitanje je sljedeće: za danu logičku formulu, koja se sastoji samo od operacija NOT, OR i AND (Slika 3. prikazuje definicije istinitosti navedenih operacija), n varijabli P₁, P₂,..., P_n, i zagrada, odrediti postoji li izbor vrijednosti istina, 1, i laž, 0, za varijable formule, tako da cijela formula ima vrijednost istina, odnosno 1. Ako takav izbor vrijednosti postoji, kažemo da je formula ispunjiva.

Slika 3.

Slika 4.

Ispitajte je li sljedeća formula ispunjiva:

Tablice istinitosti su algoritam čije je vrijeme izvršavanja eksponencijalno u odnosu na broj varijabli. Međutim, i ovdje se u polinomnom vremenu može provjeriti je li predloženo rješenje dobro!

Tako je u Primjeru 1. predloženo rješenje P₁ = 1, P₂ = 0, P₃ = 0, a testiranje se provodi samo u tri koraka!

Iz definicije slijedi da je svaki P-problem ujedno i NP-problem. Važno je istaknuti da do danas nije poznato jesu li NP-problemi ujedno i P-problemi.

Pored spomenutih primjera, problema sa zlatnicima i problema SAT, poznat je problem trgovačkog putnika, TSP (eng. travelling salesman problem). Problem TSP sastoji se od određivanja najkraćeg mogućeg puta kojim trgovački putnik mora obići određen broj gradova svraćajući u svaki grad samo jedanput, pri čemu su svaka dva grada povezana cestom, gdje su duljine cesta različite. Poznato je da je TSP također jedan NP-problem.

Važni su i tzv. NP-potpuni problemi.

O polinomnoj redukciji možete vidjeti npr. u [KR], a sve precizne definicije i objašnjenja u [DO], [KR], [SI] i [V2]. Kada bismo pronašli samo jedan NP-potpun problem koji je ujedno i P problem, pitanje "P=NP?", koje su neovisno jedan o drugom 1971. godine postavili Stephen Cook i Leonida Levin, bilo bi riješeno. Jednostavno bismo proizvoljan NP problem mogli polinomno reducirati na istaknuti NP-potpun problem (koji je dakle i P), što bi značilo da je i onaj proizvoljni sadržan u klasi P. Budući da je lako vidjeti kako je P podskup od NP, ovim bismo pokazali i obratnu inkluziju, što bi značilo da je P=NP. No, to zasad nitko nije uspio, a da problem nije nimalo lagan, govori i činjenica da je problem P vs NP uvršten u 7 milenijskih problema, te da Clay Mathematics Institute nudi milijun dolara za rješenje. Ipak, nikad se ne zna, možda ćete ga upravo vi riješiti i tako postati milijunaš!

3. SAT, logički sklopovi i dvije bitne činjenice

U ovoj ćemo točki prvo istaknuti Cook-Levinov teorem iz 1971. godine. Zatim ćemo komentirati vezu između problema SAT i logičkih sklopova.

TEOREM (Cook-Levin). Problem SAT je NP-potpun.

Dokaz teorema možete naći u [KR].

Pogledajmo sada kakva je veza između problema SAT i logičkih sklopova, odnosno krugova. Logički sklopovi sastoje se od žica i vrata. Žica prenosi vrijednost koja je 0 (laž) ili 1 (istina). Vrijednosti putuju dok ne dođu do kraja žice ili do vrata. U vrata ulazi jedna ili dvije žice, ovisno o vrsti vrata. Tu se računa nova vrijednost koja je ponovno istina ili laž, opet ovisno o vrsti vrata i vrijednostima ulaznih žica. Iz svakih vrata izlazi jedna žica kojom putuje novodobivena vrijednost. U vrata NOT ulazi jedna žica i izlazna vrijednost je laž ako i samo ako je ulazna istina. Vrata OR i AND imaju dvije ulazne žice. Izlazna vrijednost kod OR je laž ako i samo ako su obje žice nosile lažne vrijednosti, dok je kod AND rezultat istina ako i samo ako su obje ulazne vrijednosti bile istine. Dakle, potpuno analogno kao kod logičkih formula. Tomu u prilog, za svaku logičku formulu postoji ekvivalentan logički sklop, i obratno. Tako logičkoj formuli ((NOT A) AND B) OR B odgovara logički sklop prikazan na Slici 5.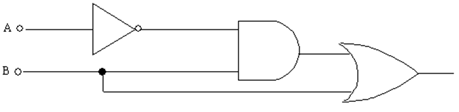

Slika 5.

Stoga je potpuno opravdano problem SAT formulirati na sljedeći način: za dani logički krug, sastavljen od nekoliko ulaznih žica, vrata i jedne izlazne žice, treba pronaći kombinaciju vrijednosti ulaznih žica, tako da se u izlaznoj žici nalazi vrijednost 1.
Na kraju poglavlja ističemo dvije bitne činjenice, na koje ćemo se kasnije pozvati.

(1) Ako je neki problem u klasi NP, tada je svaki problem koji se može polinomno reducirati na njega također u NP.

(2) Ako je dani NP-potpun problem polinomno reducibilan na neki drugi promatrani NP-problem, onda je i taj drugi NP-problem NP-potpun.

4. Što je Minesweeper problem?

Konačno, što je Minesweeper problem?

Dana je pravokutna tablica čija su polja označena u skladu s oznakama opisanima u uvodu. Dakle, neka su polja prazna, neka sadrže broj od 0 do 8, neka su prepoznata kao minirana, a neka su još neoznačena. Minesweeper problem glasi:

Slika 6. prikazuje situaciju u kojoj su dani podaci konzistentni, polja označena s 1 su oko mine * kako i treba biti, pa se odmah vidi da su desna neotkrivena polja neminirana, što znači da nema nikakve proturječnosti. Na Slici 7. nije tako, jer po pravilima igre, na mjestu 0 pokraj 1 treba stajati upravo 1, a ne 0.

Slika 6.

Slika 7.

Zadatak 2. Je li stanje na Slici 8. konzistentno? Pronađite, ako je moguće, lokacije mina.

Slika 8.

Zadatak 3. Je li polje označeno upitnikom minirano (Slika 9.)?

Slika 9.

Znajući odgovor na pitanje konzistentnosti, spretnim testiranjem odgovarajućih situacija u tablici brže otkrivamo skrivene mine i time uspješnije privodimo igru kraju. Kako razviti dobru strategiju igranja, pogledajte u [K1].

5. Zašto je Minesweeper problem NP-potpun?

Budući da je SAT u klasi NP, pogledajmo kako se pravila i konkretne situacije igre mogu opisati pomoću logičkih sklopova, te time vidjeti polinomnu redukciju Minesweepera na SAT. Promotrimo sljedeću tablicu (Slika 10.):

Slika 10.

Neka a_m znači da je polje a minirano te za j=1,...,8 neka a_j znači da a nije minirano, ali da je okruženo s točno j mina. Analogno za b, c, d, e, f, g, h, i. Tada se pravila igre Minesweeper za središnji kvadratić, e, mogu izreći i na sljedeći način:

1. Točno je jedna od oznaka e_m, e₀, e₁, ..., e₈ istinita.
2. Za k=0,1,...,8, ako je e_k istinito, onda je točno k od oznaka a_m, b_m, c_m, d_m, f_m, g_m, h_m, i_m istina.

Ovim se načinom dano stanje tablice može izraziti preko logičkih sklopova s 90 ulaza a_m, a₀, ..., i₈. Pretpostavimo li da je K krug sastavljen od manjih krugova za sva polja poput polja e, kombinirajući njihove izlaze u jedna AND vrata, pitanje ispunjivosti kruga K postaje ekvivalentno pitanju konzistentnosti podataka u Minesweeper problemu.

S druge strane, mogu li se pojedini logički sklopovi prikazati u "Minesweeper okruženju" i na koji način?

Slika 11.

Sliku 11. shvaćamo kao žicu koja prenosi istinitu ili lažnu vrijednost, ovisno o tome jesu li minirana polja x ili y. Zbog pravila igre moguće su samo dvije situacije: ili se u poljima x nalazi mina ili su polja y minirana. U svrhu definicije istinitosti vrijednosti koju prenosi žica, proizvoljno odaberimo smjer žice. U ovom slučaju uzmimo slijeva nadesno. Sada kažemo da je vrijednost istinita ako su x mine, odnosno lažna ako su y mine, tj. ako su minirana polja iza središnjih polja označenih s 1, s obzirom na smjer žice. Dakle, pojam istinosti vrijednosti žice definira se relativno s obzirom na smjer žice. Nadalje, žicu ćemo po potrebi morati znati saviti i razdijeliti.

Slika 12.

Slika 12. prikazuje savijenu žicu za 90°. Primijetimo da se istinitost žice ne mijenja njezinim savijanjem, tj. ako je u horizontalnom dijelu vrijednost istinita, to znači da je x mina, pa u okomitom dijelu, budući da je smjer tog dijela prema "dolje", znači da polje iznad središnje jedinice mora biti minirano, što i jest, jer je to polje označeno s x. Prešutno se uzima da su polja izvan granice žice, i idućih konstrukcija, označena s 0, tj. da su otkrivena i neminirana te da se pozicije svih miniranih polja, u oznaci *, mogu odrediti iz numeriranih susjednih polja.

Slika 13.

Na Slici 13. vidimo dijeljenje žice na tri dijela, tzv. splitter. Treba uočiti da dva izlaza nose vrijednosti iste istinitosti kao i ulaz, dok "srednji izlaz" Y nosi suprotnu istinosnu vrijednost. To se analogno provjerava kao na prethodnoj slici, pri čemu treba paziti na smjer pojedinog izlaza. Svaka žica može završiti dijelom kako je prikazano na sljedećoj slici (Slika 14.):

Slika 14.

a kombiniranjem više splittera može se dobiti proizvoljan broj izlaza samo jednog ulaza.

Slika 15.

Slika 15. predstavlja tzv. NOT vrata. Lagano se provjeri da ako je vrijednost ulaza X istina, onda je vrijednost izlaza Y laž, tj. ako je x mina, onda y nije mina. Konstrukcija AND vrata, na prvi pogled čini se dovoljnom za konstrukciju preostalih logičkih sklopova, budući da je poznato da se svaki logički sklop može izvesti samo pomoću AND i NOT vrata. No, nije sve tako jednostavno. Na primjer, kako omogućiti tzv. cross over, odnosno prelazak jedne žice preko druge, a da se pri tome ne naruši istinitost vrijednosti pojedinih žica. Rješenje je dano Slikom 16., koja prikazuje konstrukciju s pomoću tri splittera i troja tzv. XOR vrata.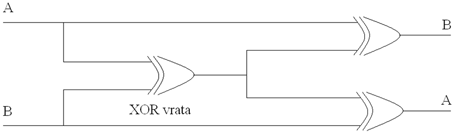

Slika 16.

S obzirom da je A XOR B istina ako i samo ako su A i B različite istinitosti, tj. A istina i B laž, ili A laž i B istina, laganom se provjerom utvrdi da su vrijednosti izlaza upravo ovakvi kako gornja slika pokazuje (npr. ako je ulaz A istina i ulaz B laž, onda je A XOR B istina, no A XOR (A XOR B) je laž, što se podudara s ulazom B, te analogno B XOR (A XOR B) istina, što odgovara ulazu A). Ekvivalentan izraz za A XOR B je NOT (NOT (A AND NOT (A AND B)) AND NOT (B AND NOT (A AND B))), čime je odmah riješen problem konstrukcije tih vrata.

Na kraju, AND vrata prikazana su sljedećom slikom:

Slika 17.

Ova vrata imaju dva ulaza, žice U i V, jednu izlaznu žicu T te istaknuto središnje polje označeno brojem 4, što je upravo i mjesto miješanja signala svih žica. Tu su i unutarnje žice R i S koje su poravnate i povezane u petlju splitterom izlaza T preko para "uređaja" a, b, c i d, e, f. Provjerimo je li zbilja vrijednost u T istina ako i samo ako su vrijednosti u U i V istinite. Prvo, ako je vrijednost u T istina, to onda znači da su polja označena s t slobodna, tj. ne sadrže mine, dok polja označena s t sadrže. Tada, zbog 3 neposredno ispod a slijedi da je s mina. Sasvim analogno, zbog simetrije slike, utvrdi se da je i r mina. Konačno, budući da su t, r, s mine, iz središnjeg istaknutog polja označenog s 4 nužno slijedi da u i v ne sadrže mine. Imajući u vidu smjer žica U i V, to točno znači da su vrijednosti u U i V istinite. Pretpostavimo sada da je vrijednost bar jedne od žica U i V lažna, odnosno da bar jedno od polja u, v nije minirano. Prema prethodnom, to znači da polje t također nije minirano, jer bi u suprotnom i u i v morali biti minirani, što je kontradikcija s pretpostavkom. Dakle, t je slobodno polje, a t minirano. Međutim, je li uopće moguća takva situacija, tj. je li uz takve pretpostavke situacija na ploči AND vrata konzistentna? Spomenuto središnje polje u tom je slučaju okruženo s još tri mine, ne računajući već označeno polje *. Stoga je barem jedno od polja r, s mina, a možda i oba. Ako je s mina, onda nije teško vidjeti da su a i c također mine (to slijedi iz susjednih polja 323), što je konzistentno s danim podacima. U slučaju da s nije mina, onda analogno slijedi da su a i b mine, a polje c slobodno, što je opet konzistentno. Zbog simetrije slike, na potpuno se isti način utvrđuje i za r. Zato, ako je barem jedna vrijednost u U i V lažna, onda je i izlaz T lažan i, ponovimo, pri tome je cijela situacija u AND vratima konzistentna. Time su objašnjena do sada najzahtjevnija, ali i najvažnija vrata.

I to nam je dovoljno, jer s pomoću svih navedenih konstrukcija u mogućnosti smo opisati logičke sklopove i krugove u tzv. "Minesweeper okruženju", te budući da se potrebni sklopovi mogu prikazati u dovoljno velikoj tablici reda N×N, gdje je N prirodan broj, vidi se da će SAT biti polinomno reducibilan na Minesweeper problem.

6. Zaključak

Dakle, Cook-Levinov teorem tvrdi da je SAT NP-potpun, iz čega odmah slijedi da je i NP-problem. Zatim, na početku poglavlja 5 vidjeli smo kako se Minesweeper problem može polinomno reducirati na problem SAT. To prema (1) iz poglavlja 3 znači da je i Minsweeper u klasi NP. Međutim, u poglavlju 5 također je objašnjeno kako se problem SAT polinomno reducira na Minesweeper problem. Napokon, zbog (2) iz poglavlja 3 slijedi da je Minesweeper problem NP-potpun.

Literatura

1. Uvod
2. P, NP i NP-potpuni problemi
3. SAT, logički sklopovi i dvije bitne činjenice
4. Što je Minesweeper problem?
5. Zašto je Minesweeper problem NP-potpun?
6. Zaključak
Literatura