Sadržaj:

0. Uvod
1. Turingov stroj
2. Varijante Turingovih strojeva
3. Halting problem
4. Izračunljive funkcije i brojevi
5. RAM i makro-stroj
6. Parcijalno rekurzivne funkcije
7. Ekvivalencija klasa RAM-izračunljivih i parcijalno rekurzivnih funkcija
Literatura

0. Uvod

U ovom članku razmatramo pojam izračunljivosti, obrađujemo neke od apstraktnih modela izračunavanja, dokazujemo njihovu ekvivalenciju i uspostavljamo vezu sa stvarnim računalima. Uvedimo na početku neke od pojmova koji će se provlačiti kroz cijeli članak.

Neka je dan neprazan skup A, koji nazivamo alfabetom, te neka se njegovi elementi zovu simbolima. Za konačan niz simbolâ alfabeta A kažemo da je riječ nad A. Riječ može biti i prazna, u oznaci ε. Skup riječi nad A nazivamo jezikom nad A. Trivijalni primjeri jezikâ su prazan skup Ø i A^*, skup svih riječi nad alfabetom A. Za svaki alfabet A i svaki jezik L nad njim vrijedi

Pritom je Aⁿ skup svih riječi duljine n nad alfabetom A. U ovom članku uzimamo da skup prirodnih brojeva N = {0, 1, 2,...} počinje nulom, što je vidljivo i iz numeracije poglavlja.

Kažemo da se (konačan ili prebrojiv) jezik L može kodirati ako postoje izračunljive funkcije code: L → N i decode: code(L) → L, takve da je code injekcija, a decode njoj inverzna bijekcija. Pojam izračunljivih funkcija definiran je u 4. poglavlju; za trenutak prihvatimo intuitivnu "definiciju" da su to funkcije čije se vrijednosti mogu izračunati kompjutorskim programom. Broj code(w) zovemo kôdom riječi w ∈ L i kraće ga označavamo s 〈w〉.

Pokažimo sada jedno od mogućih kodiranja uređenih n-torki riječi proizvoljnih jezikâ koji dopuštaju kodiranje. Neka su L₁, …, L_n jezici s kodiranjima code₁, …, code_n i neka su p₁, …, p_n prvih n prostih brojeva. Kodiranje riječi w=(w₁, …, w_n) ∈ L₁×…×L_n definiramo s

Ovako definirana funkcija očito je injekcija i, do na nepreciznu "definiciju", izračunljiva. Ako nam je zadan takav kôd, po Osnovnom teoremu aritmetike znamo da svaki pozitivan prirodan broj ima jedinstven (izračunljiv) rastav na proste faktore, pa su time jednoznačno određeni n i kôdovi sviju komponenti. Njih po pretpostavci možemo dekodirati, čime dobivamo i proceduru dekodiranja kôdova n-torki. Primijetimo da je, u ovom slučaju, moguće provjeriti je li neki prirodan broj valjan kôd neke n-torke.

1. Turingov stroj

Turingov stroj (u daljnjem tekstu: TS) fundamentalni je apstraktni model izračunavanja. Alan Turing ga je u radu [AT] ustanovio kao matematičku apstrakciju ljudskog procesa računanja. Premise su mu bile da se računanje obavlja pomoću olovke i neograničenog izvora papira na kvadratiće, svaki kvadratić sadrži najviše jedan znak neke konačne abecede, i uvijek je najviše konačno mnogo kvadratića ispunjeno. Osoba računa po danim pravilima, imajući pregled nad konačno mnogo (ali uvijek konstantom ograničeno) kvadratića istodobno. Tijekom procesa računanja mijenjaju se interna stanja svijesti, kojih je uvijek konačno mnogo, odražavajući informacije o trenutačnom tijeku proračuna. Prema tim stanjima, zadanim pravilima i zapisanim znakovima koje može vidjeti, osoba mijenja stanje svijesti i sadržaj tih kvadratića.

Deterministički Turingov stroj

Točnije, δ je parcijalna funkcija, što znači da nije nužno definirana na cijeloj domeni. O parcijalnim funkcijama bit će još govora u šestom poglavlju.

Manje formalno, Turingov stroj sastoji se od beskonačne trake i glave koja s nje čita i na nju piše simbole iz alfabeta Γ. Na početku se stroj nalazi u stanju s, a na početku inače prazne trake zapisani su ulazni podaci pomoću alfabeta Σ. Stroj radi u diskretnim taktovima. U svakom taktu glava pročita simbol s trake i, ovisno o stanju u kojem se stroj nalazi, zapiše novi simbol na traku, prijeđe u novo stanje i pomakne se na lijevo (☜), na desno (☞), ili ostane na mjestu (□). Ponašanje stroja određuje funkcija prijelaza δ. Stroj staje kada dođe u neko stanje iz skupa F i tada su na traci zapisani izlazni podaci.

U nastavku ćemo precizno opisati rad Turingova stroja i dati formalne definicije pojma trake, glave i promatranog (trenutačnog) simbola.

Komponente i konfiguracije Turingova stroja

Traka TS-a je niz ćelija. Svaka ćelija sadrži točno jedan simbol alfabeta trake. U svakom taktu samo je konačno mnogo ćelija "popunjeno", odnosno na njima piše simbol različit od bjeline. Stanje trake formalno opisujemo funkcijom tape: N × N → Γ koja za dani takt t i danu ćeliju n vraća pripadni simbol tape(t, n). Prethodni uvjet o konačno mnogo popunjenih ćelija možemo formulirati kao:

TS posjeduje glavu za čitanje i pisanje po traci. U svakom taktu glava je nad točno jednom ćelijom. Za dani takt, trenutačni simbol zapisan je u ćeliji nad kojom se nalazi glava. Formalno, funkcija head: N → N kazuje nad kojom je ćelijom glava u danom taktu, a funkcija symb: N → Γ, definirana kao symb(t) = tape(t, head(t)), daje trenutačni simbol.

U svakom taktu deterministički se TS nalazi u točno jednom stanju; formalno, imamo funkciju state: N → Q. Stanja TS-a služe imenovanju trenutačnih, pamćenju prethodnih i/ili zadavanju budućih akcija. Za praktične primjene pogodna su deskriptivna imena stanja, no za teorijska razmatranja bitno ih je samo razlikovati, tj. skup stanja možemo identificirati s početnim segmentom prirodnih brojeva duljine |Q|.

Slične primjedbe vrijede i za alfabet. Dok je u praksi korisno uzeti alfabet što sličniji onom kojim izričemo problem koji stroj rješava, za teoriju je pogodno fiksirati jedinstveni simbol bjeline za sve strojeve te numerirati ostale simbole i predstaviti ih prirodnim brojevima. Bez smanjenja općenitosti smijemo odabrati bazu 2, odnosno simbole 0 i 1, kao okosnicu alfabeta svakog TS-a.

Za dani takt, trenutačna konfiguracija TS-a u potpunosti opisuje stanje stroja. Konfiguracija pamti trenutačno stanje, poziciju glave i sadržaj trake (prema rečenom, dovoljno je pamtiti sadržaje konačno mnogo ćelija na kojima nisu bjeline). Formalno, cfg: N → N zadana je kao funkcija takta:

Iz rečenog slijedi da je TS-ove moguće kodirati kao sedmorke njihovih definicijskih komponenti i tim se kôdovima služiti kao njihovim cjelovitim opisom, tj. desc(M)  =〈M〉, gdje je M = (Q, Σ, Γ, _, s, F, δ). Sad je odmah vidljivo da postoji prebrojivo mnogo različitih Turingovih strojeva.

Rad Turingova stroja

Primijetimo da je za svaki t ∈ N funkcija n  tape(t, n) niz u Γ. Posebnost tog niza za t = 0 je u tome što nije posljedica rada stroja, već ga zadaje korisnik. Preciznije, korisnik upisuje riječ (možda i praznu) nad ulaznom abecedom Σ na uzastopne ćelije trake, počev od nulte. Ostatak trake je popunjen bjelinama. Ta upisana riječ zove se ulazom (eng. input).

Smatramo da stroj, nakon što je primio ulaz, započinje s radom u nultom taktu, uvijek s istim početnim uvjetima.

Ako je state(t) ∈ F, kažemo da stroj staje, te zapis na traci zovemo izlazom (eng. output) stroja. U protivnom, uvedimo (općenito parcijalnu) funkciju Δ(t) := δ(state(t), symb(t)). Ako je Δ definirana u t, tada je prijelaz u idući takt opisan sljedećim jednadžbama. Komponente od Δ(t) označavamo redom s Δ(t)₀,  Δ(t)₁  i  Δ(t)₂.

Ako Δ nije definirana za dani t (jer δ nije definirana na odgovarajućem paru stanja i simbola), tada ponašanje stroja nije specificirano, osim što utvrđujemo da stroj više nikada ne može stati. Formalno, u takvoj situaciji konfiguracija stroja ostaje nepromijenjena: cfg(t) = cfg(t + 1). Stroj upada u beskonačnu petlju koju sâm ne može niti detektirati niti prekinuti, stoga nikad ne može stati nakon što se u njoj zatekne.

Ukratko, TS u svakom koraku pročita trenutačni simbol s trake, te u ovisnosti o njemu i trenutačnom stanju, konzultiravši funkciju prijelaza δ, prelazi u novo stanje, piše novi simbol na promatranu ćeliju (koji može biti identičan starom), te miče glavu jedno mjesto ulijevo ili udesno, ili je ostavlja na staroj poziciji.

Primijetimo da se ostavljanje glave na mjestu uvijek može simulirati dodatnim stanjima i pravilima prijelaza, ako raspolažemo strojem koji obvezno mora micati glavu. Također, slučaj kad bi se glava, prema pravilima, trebala pomaknuti ulijevo s nulte ćelije tretiramo kao neizvršiv, odnosno glava ostaje na mjestu. Uz specijalni ulazni simbol kao "marker" početka trake i prikladna pravila, taj slučaj uvijek možemo izbjeći.

Zadavanje Turingova stroja

Funkcija prijelaza δ predstavlja "program" za naš TS, pa je svaki TS u biti evaluator svoje (općenito parcijalne) funkcije prijelaza - svojeg programa. Ako "programiranje" shvatimo kao "djelatnost pisanja programâ", pokazat ćemo dva ekvivalentna načina programiranja Turingovih strojeva na primjeru TS-a koji povećava ulazni broj u binarnom zapisu za 1, s tim da zapis počinje najmanje značajnim bitom. Svako od njih svodi se na zadavanje sviju komponenti definicijske sedmorke, od kojih je najzanimljivija upravo δ.

Turingov stroj za povećavanje binarnog broja

Q = { s0, s1, s2 }		δ(s0, _) = (s2, _, □)
Σ = { 0, 1 }		δ(s0, 0) = (s0, 1, ☞)
Γ = Σ ∪ { _ }		δ(s0, 1) = (s1, 0, ☞)
s = s0		δ(s1, _) = (s2, 1, □)
F = { s2 }		δ(s1, 0) = (s0, 1, ☞)
		δ(s1, 1) = (s1, 0, ☞)

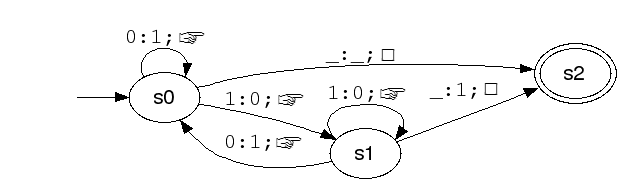
U desnom stupcu vidimo tablično zadanu funkciju prijelaza, koja je na slici ispod prikazana usmjerenim labeliranim grafom, čiji čvorovi predstavljaju stanja stroja. Početno stanje označeno je strelicom bez izvora, a završno je zaokruženo dvaput. Bridovi predstavljaju moguće tranzicije među stanjima, i označeni su trenutačnim simbolom, novim simbolom koji će biti zapisan, te pomakom glave. Sličan je prikaz uvriježen i za mnoge druge klase automata, kao što su konačni ili push-down automati.

Za daljnje primjere i programske zadatke čitatelje upućujemo na simulatore Turingovih strojeva [AV] ili [DS]. Još dva primjera za prvi simulator možete preuzeti kao Turing.zip.

Poznavajući opis nekog stroja i bilo koju njegovu konfiguraciju, uvijek možemo nastaviti njegov rad, no pokazat ćemo da, u potpunoj općenitosti, ta dva podatka nisu dovoljna da bismo unaprijed saznali globalno ponašanje bilo koje od funkcija tape, head i cfg.

2. Varijante Turingovih strojeva

Turingovi strojevi definiraju se na mnogo različitih načina. Upoznat ćemo neke i vidjeti da su, što se tiče rješivosti problemskih instanci, sve te definicije ekvivalentne. Ipak, neki su modeli Turingovih strojeva "brži" od drugih na raznim klasama problema, što je inspiriralo teoriju složenosti (engl. complexity theory). U njezinu se razradu ovdje nećemo upuštati.

Jedno od najčešćih proširenjâ pojma TS-a su strojevi s trakom neograničenom slijeva. Točnije, traka je funkcija tape' : N × Z → Γ, dok head poprima vrijednosti u cijelim brojevima. Taj je slučaj u literaturi ili osnovni, ili se svodi na naš pojam TS-a na razne načine. Jedna mogućnost je definirati novi stroj M' s poluomeđenom trakom, proširivši ulazni alfabet posebnim markerom koji će biti zapisan isključivo na nultoj ćeliji, te definirati novi skup stanja Q' = Q × { 1-, 0-, 0+, 1+ }. Stroj M' koristi parne ćelije za nenegativne ćelije polazne trake, a neparne za negativne ćelije. Novi stroj pomiče glavu ili za dvije ćelije u nekom od smjerova, ili je ostavlja na mjestu, obilazeći tako točno parne, odnosno točno neparne ćelije. Dodatne oznake svakog od stanja polaznog stroja sastoje se od dva simbola. Prvi služi lakšem pomicanju za dva mjesta i govori koliko se još mjesta treba pomaknuti (0 ili 1), a drugi kazuje nalazimo li se na ćeliji koja odgovara polaznoj negativnoj ili nenegativnoj ćeliji (- ili +). Do prijelaza s parnih na neparne, tj. nenegativnih na negativne ćelije dolazi točno onda kad bi se glava trebala pomaknuti ulijevo s nulte ćelije. Naravno, pomaci polaznog stroja udesno i ulijevo dok se nalazi na negativnom dijelu svoje trake, mijenjaju smjer u novom stroju M'. Uz ove modifikacije polazne relacije prijelaza lako se uvjeriti da novi stroj staje točno kad i polazni i daje isti izlaz.

Time je riješeno pitanje omeđenosti trake. No, TS može imati i više od jedne trake, a da time ne postaje moćniji. Svaka od novih traka ima svoju glavu, koja se miče neovisno o ostalima. Obično se prva traka koristi samo za ulaz, a katkad se smatra da se nakon početka rada više ne smije mijenjati. Pokazuje se da takve višetračne TS-ove možemo simulirati jednotračnim, slično kao što smo stroj s obostrano neograničenom trakom simulirali strojem s jednostrano neograničenom trakom. Dokaz se nalazi u knjigama [MS], [CP] i u diplomskom radu [IK].

Poseban i važan slučaj TS-ova predstavljaju strojevi kod kojih je skup završnih stanja F = {A, R} dvočlan, pri čemu A zovemo stanjem prihvaćanja, a R stanjem odbacivanja. Korisnik po završnom stanju interpretira prihvaća li takav TS ulaznu riječ ili ne, već prema tome je li stroj završio u stanju prihvaćanja ili odbacivanja.

Neka je M proizvoljni TS s takvim skupom završnih stanja. Jezik L(M) definiramo kao skup svih riječi nad ulaznim alfabetom Σ stroja M koje on prihvaća.

Za jezik L nad alfabetom Σ kažemo da je rekurzivan ili Turing-odlučiv, ako postoji Turingov stroj M s ulaznim alfabetom Σ koji ulaznu riječ w nad Σ prihvaća točno kad je w ∈ L, a u suprotnom je odbacuje. Kraće rečeno, M odlučuje jezik L, tj. L = L(M).

Za jezik L nad alfabetom Σ kažemo da je rekurzivno prebrojiv ili Turing-prepoznatljiv, ako postoji Turingov stroj M' s ulaznim alfabetom Σ, koji ulaznu riječ w nad Σ prihvaća točno kad je w ∈ L, a u suprotnom je ili odbacuje ili nikada ne staje. Kraće rečeno, M' prepoznaje jezik L.

Očito je svaki rekurzivan jezik ujedno rekurzivno prebrojiv, no obrat ne vrijedi. Objašnjenje i primjere na trenutak odgađamo, a sad pokazujemo intuiciju iza pojma "biti rekurzivno prebrojiv jezik".

Neka je L rekurzivno prebrojiv jezik nad Σ, a M neki TS koji ga prepoznaje. Konstruirajmo Turingov stroj E (enumerator), koji ispisuje sve riječi iz L. Stroj E započinje rad praznom trakom i nekim redom generira sve riječi nad Σ. Primijetimo da je to uvijek moguće, jer je Σ konačan te se stoga može dobro urediti, pa možemo npr. generirati riječi u leksikografskom poretku. Za i-tu riječ, E stavlja redom sve riječi do uključivo i-te na ulaz od M, te na svakom ulazu simulira M najviše i koraka. Ako M prihvati riječ, E je ispisuje. Time E testira sve riječi nad Σ za svako moguće konačno izvršavanje od M, i tako enumerira jezik L.

Obratno, postoji li enumerator za neki jezik, možemo definirati TS koji uspoređuje dani ulaz s enumeriranim riječima i prihvaća ga naiđe li na poklapanje.

Nedeterministički Turingov stroj

Sve spomenute varijante TS-a bile su determinističke, tj. jednom paru stanja i simbola odgovaralo je najviše jedno iduće stanje i najviše jedna akcija na traci (odnosno, kombinirana akcija na više traka). Nedeterministički Turingov stroj (u daljnjem tekstu: NTS) radikalni je odmak od tog principa, kao što je, da povučemo ne posve neosnovanu analogiju sa stvarnošću, masivno paralelno računalo znatno kompleksniji i moćniji sustav od klasične sekvencijalne arhitekture.

Postoje mnoge intuitivne interpretacije ovako zadane funkcije prijelaza, od kojih je možda najzornija sljedeća. Za dano stanje i pročitani simbol postoji skup akcija koje će uslijediti. Svaka akcija prevodi stroj u novo stanje, piše neki simbol na traku i pomiče glavu neovisno o, ali istodobno s drugim akcijama. Kako je to moguće? Zamislimo da se za svaku od tih akcija stroj "klonira", tako da strojevi-djeca dobivaju identičan sadržaj trake, trenutačno stanje i poziciju glave kao u roditelja. Svaki stroj-dijete vrši svoju akciju i potom primjenjuje funkciju prijelaza, koja može rezultirati novim kloniranjima. Opisana interpretacija u potpunosti odgovara standardnoj POSIX semantici fork(2) sistemskog poziva.

Svako izračunavanje determinističkog Turingova stroja na danom ulazu je (možda konačan) niz njegovih konfiguracija, indeksiran taktom. Izračunavanje nedeterminističkog stroja je stablo (možda konačno), čiji su nivoi indeksirani taktom. Na svakom nivou nalazi se skup trenutačnih konfiguracija, za svaki aktivni "klon" po jedna. Svaka konfiguracija može imati najviše konačno potomaka prve generacije, preciznije, ne više od p :=  |Q × Γ × {☜, □, ☞}|.

Korijen tog stabla čini početna konfiguracija. Maksimalni putovi u stablu, koji započinju korijenom i ne mogu se nastaviti novim konfiguracijama jer je dostignuto jedno od završnih stanja, predstavljaju jedno moguće determinističko izračunavanje na danom ulazu. Za konačan maksimalni put kažemo da je terminirajuće izvršavanje. U ovim terminima NTS prihvaća ulaz ako postoji barem jedno terminirajuće izračunavanje koje rezultira stanjem prihvaćanja. NTS odbacuje ulaz ako su sva izračunavanja terminirajuća i rezultiraju stanjem odbacivanja.

Očito, svaki TS ujedno je i NTS, no mnogo je zanimljivije da se svaki NTS može simulirati determinističkim strojem. Dokaz je dugačak i tehnički, pa ga izostavljamo. Možete ga naći npr. u [MS], [CP] ili u [IK].

Univerzalni Turingov stroj

Upoznali smo se sa simulacijama jednog stroja drugim. Postavlja se pitanje postoji li stroj koji može simulirati svaki TS? Alan Turing odgovorio je u članku [AT] potvrdno, dajući jednu moguću konstrukciju.

Postoji Turingov stroj U takav da za svaki Turingov stroj M i bilo koju riječ w nad njegovom abecedom vrijedi: stroj U s ulazom〈(M, w)〉staje ako i samo ako staje stroj M s ulazom w i pritom oba stroja daju isti izlaz. Za U kažemo da je univerzalni Turingov stroj.

Redovno se pojavljuju sve jednostavniji (u smislu broja stanja i simbola) univerzalni TS-ovi. Jedan univerzalni TS nudi spomenuti paket simulatorâ [AV].

Važnost univerzalnog Turingova stroja ne može biti precijenjena. Stroj U može izračunati svaku Turing-izračunljivu funkciju, odlučiti svaki rekurzivan jezik i prepoznati svaki rekurzivno prebrojiv jezik. Usporedimo li TS-ove s kompjutorskim programima u nekom programskom jeziku, tada je U program koji zna izvršavati sve takve programe, tj. analogon interpretera ili virtualne mašine. Ali ni U ne može sve!

3. Halting problem

Zapitajmo se sljedeće: postoji li Turingov stroj H koji radi kao "automatski verifikator"? Za bilo koji Turingov stroj M i njegov ulaz w, stroj H odlučuje prihvaća li M riječ w. Ekvivalentno pitanje je da li je jezik L = {〈(M, w)〉|  M je Turingov stroj koji prihvaća w} rekurzivan? Odgovor je da takav stroj H ne postoji, tj. jezik L nije rekurzivan. No, L jest rekurzivno prebrojiv jer ga univerzalni Turingov stroj U prepoznaje. Time dobivamo i primjer rekurzivno prebrojiva jezika koji nije rekurzivan. Pokažimo sada da takav Turingov stroj H ne postoji!

Bez smanjenja općenitosti možemo pretpostaviti da svi Turingovi strojevi u dokazu svoj ulaz kodiraju prirodnim brojevima, prihvaćanje ulaza signaliziraju izlazom 1, a odbacivanje izlazom 0. Označimo binarni komplement znakom "tilda": ˜0=1, ˜1=0. Ako pretpostavimo da Turingov stroj H postoji, tada je njime definirana funkcija

Definirajmo novi Turingov stroj D s

Stroj D možemo shvatiti kao "dijagonalni komplement". Turingovih strojeva ima prebrojivo mnogo, pa je skup svih TS-ova moguće dobro urediti. Stroj H inducira beskonačnu 0-1 matricu kojoj su retci indeksirani Turingovim strojevima, a stupci pripadnim opisima. U danom retku M_i i stupcu 〈M〉_j piše prihvaća li M_i riječ 〈M〉_j, tj. H(M_i,〈M〉_j). Stroj D komplementira vrijednosti na dijagonali te matrice.

Što se zbiva kad D primijenimo na njegov vlastiti opis? Ako D prihvaća 〈D〉, tada je D(〈D〉) = 0, tj. trebao bi ga odbaciti. Ako D odbacuje 〈D〉, tada je D(〈D〉) = 1, tj. trebao bi ga prihvatiti. U oba slučaja imamo kontradikciju, pa stroj D ne može postojati, a onda niti stroj H.

Riceov teorem

Iz nemogućnosti rješavanja ovog tzv. "halting problema" izvire mnoštvo drugih Turing-neodlučivih problema. Velik broj njih može se promatrati kao specijalan slučaj Riceova teorema:

Jezik P iz izreke teorema možemo shvatiti kao opis nekog svojstva Turingovih strojeva, u smislu da P sačinjavaju kodovi onih strojeva koji imaju to svojstvo. Kad bi P bio odlučiv, postojao bi Turingov stroj koji bi za kôd proizvoljnog Turingova stroja 〈M〉 odlučio sadrži li P taj kôd, odnosno ima li M svojstvo reprezentirano s P.

Prva pretpostavka teorema kaže da promatramo svojstvo za koje nije važno kako realiziramo ("programiramo") i kako kodiramo strojeve, ako su jezici tih strojeva isti. Druga pretpostavka kaže da P nije prazan jezik i ne sadrži kôdove svih mogućih strojeva, tj. promatrano svojstvo nije trivijalno. Dakle, netrivijalna svojstva Turingovih strojeva su neodlučiva! Jedno takvo svojstvo, koje ne ovisi o "implementaciji" niti kodiranju, upravo je pitanje zaustavljanja na danom inputu.

4. Izračunljive funkcije i brojevi

Što Turingovi strojevi zapravo računaju? Bez smanjenja općenitosti možemo smatrati da na ulazu stoji neki prirodan broj, a na izlazu konačan niz nula i jedinica. Tako svaki TS računa pripadnu parcijalnu funkciju f iz N u {0, 1}^*. Ako TS ne staje za neki prirodan broj na ulazu, smatramo da funkcija f nije definirana za taj broj. Kako je svaki jezik podskup svih riječi nad danim alfabetom, može ga se predstaviti njegovom karakterističnom funkcijom, pa je uistinu svaki TS evaluator neke funkcije ovog oblika.

Za parcijalnu funkciju f iz N u {0, 1}^* kažemo da je Turing-izračunljiva ako postoji Turingov stroj koji je izračunava.

Za realni broj 0 ≤ a < 1 kažemo da je Turing-izračunljiv ako se može po volji dobro aproksimirati nekom Turing-izračunljivom funkcijom. Preciznije, ako izlazni niz TS-a shvatimo kao znamenke iza decimalne točke u binarnom zapisu pravog razlomka, tada kažemo da je a Turing-izračunljiv ako postoji Turing-izračunljiva funkcija, koja za svaku pozitivnu racionalnu apsolutnu pogrešku ε vraća racionalan broj r takav da je |r - a| ≤ ε. Proizvoljan realan broj je Turing-izračunljiv ako su mu izračunljivi cijeli i dio iza decimalne točke. Kompleksan broj je Turing-izračunljiv ako su mu realni i imaginarni dio Turing-izračunljivi realni brojevi.

Moguće je konstruirati TS-ove koji, primivši ε-pogrešku i opise strojeva koji računaju dva broja a i b, vraćaju kao rezultat a ? b do na ε-pogrešku, gdje je "?" neka od četiri osnovne računske operacije +, −, * i / (pri čemu je za operaciju dijeljenja "/" broj b≠0). Time dobivamo da Turing-izračunljivi brojevi tvore polje.

Navedimo bez dokaza neka od svojstava Turing-izračunljivih funkcija i brojeva iz Turingova članka [AT].

1. Kompozicija (dviju, pa i konačno mnogo) Turing-izračunljivih funkcija je Turing-izračunljiva.
2. "Rekurzija čuva izračunljivost": ako je r cijeli broj, a φ(m, n) Turing-izračunljiva funkcija, tada je funkcija η definirana s η(0) = r,  η(n) = φ(n, η(n - 1)) Turing-izračunljiva.
3. Ako je φ Turing-izračunljiva funkcija čije su vrijednosti uvijek 0 ili 1, tada je broj čija je n-ta binarna znamenka iza decimalne točke jednaka φ(n) Turing-izračunljiv.
4. Ako su α < β Turing-izračunljivi realni brojevi, a φ Turing-izračunljiva rastuća neprekidna funkcija i ako vrijedi φ(α) < 0 < φ(β), tada postoji jedinstveni Turing-izračunljiv realni broj γ takav da je α < γ < β, te φ(γ) = 0 (tj. φ ima Turing-izračunljivu nultočku).

Iz posljednjeg svojstva slijedi da su svi algebarski brojevi Turing-izračunljivi (kao nultočke polinomâ s cjelobrojnim koeficijentima). Pokazuje se da su neki transcendentni brojevi, na primjer π i e, također Turing-izračunljivi. No, budući da Turingovih strojeva ima prebrojivo mnogo, a realnih brojeva neprebrojivo, postoje realni brojevi koji nisu Turing-izračunljivi.

Evo jednostavnih primjera cjelobrojnih funkcija koje nisu Turing-izračunljive. Već smo napomenuli da bez smanjenja općenitosti možemo za alfabet svih Turingovih strojeva uzeti binarne znamenke. Definiramo tzv. Busy beaver funkcije:

1. Σ(n): najveći broj jedinica koje može ispisati Turingov stroj s n stanja prije nego što stane.
   
   
2. S(n): najveći broj taktova koje može odraditi Turingov stroj s n stanja prije nego što stane.

Iako se znaju neke vrijednosti ili ocjene tih funkcija, one su općenito neizračunljive (zapravo, "neuhvatljive", jer rastu brže od bilo koje Turing-izračunljive funkcije). Kad bi npr. S bila izračunljiva, tada bi znali da svaki Turingov stroj s n stanja, ako nije stao u S(n) koraka, nikada neće stati. Dakle, mogli bismo simulirati prvih S(n) taktova bilo kojeg TS-a i odlučiti staje li na danom ulazu. Time bismo riješili Halting problem, što je nemoguće.

Jedan od spektakularnijih primjera neizračunljivih realnih brojeva svakako je Chaitinova konstanta Ω. Za dani model izračunavanja, reprezentaciju i kodiranje strojeva, odnosno programa tog modela, postoji zasebna konstanta koja govori kolika je vjerojatnost da slučajno odabrani program staje. Može se pokazati da, iako su poznate neke početne znamenke, niti jedna Chaitinova konstanta nije izračunljiva jer bi u suprotnom mogli riješiti Halting problem.

Church-Turingova teza

Teza je tvrdnja koja se ne može dokazati, jer pojmovi nisu strogo definirani, ali se može oboriti. Teza Church-Turinga povezuje intuitivni pojam izračunljivosti s precizno definiranim pojmom Turing-izračunljivosti i tvrdi da su izračunljive funkcije one i samo one koje su ujedno i Turing-izračunljive. Dosad nije pronađena niti jedna funkcija za koju bi se svatko složio da je izračunljiva, ali za nju dokazano ne postoji pripadni Turingov stroj. Štoviše, pokazano je da su svi "razumni" modeli izračunavanja ekvivalentni Turingovim strojevima (Turing-potpuni), u smislu da računaju točno Turing-izračunljive funkcije. Često se govori samo o pojmu izračunljivosti, zajedničkom svim tim modelima.

Uzmemo li tezu kao istinitu, za dokazati Turing-potpunost nekog programskog jezika ili apstraktnog modela izračunavanja dovoljno je pokazati (najčešće efektivnom konstrukcijom) da je u njemu moguće simulirati univerzalni Turingov stroj. Obrat je zanimljiv u slučajevima kad se model izračunavanja čini jačim od TS-a, kao što smo pokazali na primjeru nedeterminističkog TS-a.

Iako su predloženi neki modeli izračunavanja koji su uistinu jači od Turingovih strojeva, niti jedan ne odgovara temeljnoj intuiciji Alana Turinga o simulaciji ljudskog procesa računanja. Čitatelje zainteresirane za šire upozavanje s djelom Alana Turinga upućujemo na najnoviji broj časopisa Notices of the American Mathematical Society, koji mu je gotovo u potpunosti posvećen.

5. RAM i makro-stroj

S Turingovih prelazimo na RAM-strojeve. Random Access Machine apstrakcija je pojednostavljenog stvarnog sekvencijalnog računala.

Centralni procesor sekvencijalnog računala sastoji se, među ostalim, od sljedećih komponenti:

• skupa instrukcija koje prepoznaje, te logike za njihovo dekodiranje i izvršavanje;
• skupa imenovanih registara iz kojih izravno čita, odnosno, u koje izravno zapisuje podatke;
• sučelja prema vanjskoj memoriji s izravnim pristupom;
• posebnog registra koji sadrži adresu instrukcije u vanjskoj memoriji koja se sljedeća izvršava, te mehanizma za njegovo automatsko povećavanje za 1. Taj registar nazivamo programskim brojilom.

RAM-stroj posjeduje prebrojivo mnogo registara, imenovanih prirodnim brojevima, od kojih svaki sadrži točno jedan po volji velik prirodan broj. Također, ima i vanjsku memoriju s izravnim pristupom koju može samo čitati. Vanjska memorija također ima prebrojivo mnogo ćelija, adresiranih prirodnim brojevima. Svaka ćelija sadrži točno jednu instrukciju RAM-stroja. Skup instrukcija RAM-stroja nije standardiziran. Za teoretska razmatranja često se uzimaju samo sljedeće tri instrukcije:

1. inc i,   gdje je i ime nekog registra RAM-stroja;
   
   
2. dec R_i, k,   gdje je i ime nekog registra RAM-stroja, a k adresa neke ćelije vanjske memorije;
   
   
3. goto k,   gdje je k adresa neke ćelije vanjske memorije.

Program za RAM-stroj je neprazan i konačan niz RAM-instrukcija. Kao što računalo može izvršavati razne programe, isto vrijedi i za RAM-stroj. RAM-program smješta se u vanjsku memoriju stroja na uzastopne ćelije, počev od nulte. Na preostalim ćelijama možemo smatrati da stoji posebna instrukcija halt, nedopuštena unutar RAM-programa.

RAM-stroj posjeduje i programsko brojilo, koje adresira instrukciju koja će se sljedeća izvršiti. Programsko brojilo prije početka izvršavanja RAM-programa ima vrijednost 0, a u konačno mnogo uzastopnih registara, počev od nultog, upisuju se brojevi koji predstavljaju ulaz danog programa. Možemo smatrati da u preostalim registrima piše broj 0.

RAM-stroj radi u diskretnim taktovima. U svakom taktu izvršava se točno jedna RAM-instrukcija, na sljedeći način.

1. Dohvati instrukciju s adrese iz programskog brojila.
   
   
2. Uvećaj programsko brojilo za 1.
   
   
3. Ako je dohvaćena instrukcija:
   
   
   • halt,  prekini s radom. Smatramo da vrijednost nultog registra predstavlja izlaz danog RAM-programa.
     
     
   • inc R_i,  povećaj vrijednost u registru i za 1 ("inkrement").
     
     
   • dec R_i, k,  provjeri piše li u registru i vrijednost strogo veća od 0.
     • Ako da, smanji vrijednost u registru i za 1 ("dekrement").
     • Ako ne, postavi vrijednost programskog brojila na k.
     
     
   • goto k,  postavi vrijednost programskog brojila na k.

Ova shema sačinjava jedan takt i ponavlja se dokle god stroj nije stao.

Primijetimo da se registrima pristupa isključivo navođenjem njihova imena, pa je za svaki RAM-program poznat broj registara kojima program pristupa (nazovimo ga m). Uz prikladno preimenovanje registara, smatramo da je riječ o prvih m registara.

Nadalje, neka je n broj instrukcija danog RAM-programa. Reći ćemo da je program valjan ako niti u jednoj instrukciji uvjetnog ili bezuvjetnog skoka ne sadrži adresu memorijske ćelije veće ili jednake n kao cilj skoka. Slijedi da valjani RAM-program završava ako i samo ako se u programskom brojilu nađe n. To se može promatrati kao ograničen adresni prostor programa: čitanje programu nepripadajuće memorije nije dopušteno.

Instrukcijama pridružujemo kodove na sljedeći način:

Jasno je da i svakom RAM-programu možemo pridružiti kod. Uočimo da tu nema ničeg čudnog: instrukcije se u stvarnim računalima prezentiraju binarnim kôdovima, a njihova konkatenacija, uz još neke dodatke, predstavlja izvršni program. Ulaz RAM-stroja, kao konačan, možda i prazan niz brojeva, te izlaz, kao jedan broj, također se mogu kodirati.

Neka je dan valjani RAM-program p i neki njegov ulaz w. Konfiguracija RAM-stroja u taktu t za program p i ulaz w uređeni je par vrijednosti programskog brojila na početku tog takta i vrijednosti svih m_p registara kojima program pristupa. Završna konfiguracija je konfiguracija u trenutku kad stroj stane, tj. kad programsko brojilo poprimi vrijednost n. Izračunavanje RAM-programa na danom ulazu je niz konfiguracija, indeksiranih taktom, od kojih svaka slijedi iz prethodne prema gore opisanoj shemi izvršavanja. Niz je konačan ako i samo ako postoji završna konfiguracija - za takvo izračunavanje kažemo da je terminirajuće. Očito se i konfiguracije i terminirajuća izvršavanja mogu kodirati.

Pokažimo kako možemo obogatiti instrukcijski skup RAM-stroja bez da povećamo klasu rješivih problema. Uvedimo instrukciju dek kao dekrement s uvjetnim skokom, koja se ponekad koristi umjesto dec. Ostatak sintakse je identičan, a semantika je donekle ortogonalna: ako u promatranom registru stoji vrijednost 0, tada prijeđi na sljedeću instrukciju, inače smanji vrijednost registra za 1 i skoči na zadanu adresu. Ako se dek R_i, k instrukcija nalazi na adresi j, možemo je zamijeniti sljedećim dvjema osnovnim instrukcijama:

Vidimo da ovakvim zamjenama i prikladnim prenumeriranjem instrukcija možemo svesti sve programe koji koriste dek na oblik koji koristi samo tri osnovne instrukcije.

Pokažimo primjer RAM-programa koji će nas uvjeriti da se instrukcija pridruživanja vrijednosti jednog registra drugome može realizirati postojećim modelom.

Prve dvije instrukcije poništavaju nulti i drugi registar. Potom se u petlji smanjuje vrijednost prvog, te povećava vrijednost nultog i drugog registra. Zatim se u još jednoj petlji vraća početna vrijednost prvog registra. Posljednja instrukcija služi samo za legalan izlazak iz programa.

Mogli bismo nastaviti s primjerima, ali bi programi brzo postali preglomazni. Stalno bi se ponavaljali obrasci za trivijalne radnje, poput ovog kopiranja vrijednosti. Da bi se tome doskočilo, uveden je koncept makro-stroja. Makro-stroj identičan je RAM-stroju, do na "pretprocesiranje" programa. Naime, neka je q postojeći RAM-program, čiju bismo funkcionalnost rado iskoristili u novom programu p. To je najlakše napraviti umetnemo li poziv programa q u program p i pritom naznačimo koji registri predstavljaju ulaz za q. Koncept je vrlo sličan makroima pretprocesora programskog jezika C, odnosno ideji tzv. inline funkcija kod kojih se poziv funkcije zamjenjuje njezinim tijelom.

Svaki algoritam zamjene poziva makroa njegovim tijelom mora paziti na pravilno prenumeriranje instrukcija u pozivatelju i makrou. Nadalje, u makrou se vežu registri pozivatelja na odgovarajuće registre makroa, i to oni i samo oni registri pozivatelja koji su eksplicitno navedeni u pozivu. Ostali registri makroa preimenuju se u dotad nekorištene registre stroja.

Uvedimo jedan jednostavan program koji će se pokazati dosta korisnim kao makro. Neka se zove zero i neka poništava nulti registar.

Pokažimo uporabu makroa na primjeru programa add, koji zbraja vrijednosti prvog i drugog registra te rezultat sprema u nulti registar. Koristi se makro move … using, koji se može realizirati slično kao prethodno definiran makro move.

Možemo iskoristiti ovo zbrajanje da bismo njime definirali množenje, njime pak potenciranje i tako dalje. Sintaksu za poziv makroâ ovdje nećemo precizirati. Čitatelje zainteresirane za programiranje za makro-stroja upućujemo na simulator s primjerima u programskom paketu MaMa [DN] od autorâ ovog članka.

Rekli smo da valjani RAM, pa tako i makro-program ima samo jedan način da stane. No, lako se vidi da postoji i samo jedan način da ne stane: da se zavrti u beskonačnoj petlji. RAM-stroj zapravo računa funkcije koje uređenim k-torkama prirodnih brojeva pridružuju prirodne projeve (gdje k ovisi o programu, a ne o stroju). Ako program upadne u beskonačnu petlju, smatramo da funkcija koju izračunava nije definirana na danom ulazu.

Makro-stroj ekvivalentan je RAM-stroju po konstrukciji. No, RAM-stroj dopušta i "oslabljenje", u smislu da je dovoljno konačno mnogo, ali barem dva registra. Takvi RAM-strojevi s konačno mnogo registara često se nazivaju Minskyjevim strojevima. Pokazuje se da su oni također ekvivalentni RAM-stroju. U formalni dokaz se nećemo upuštati, ali tvrdnja slijedi zbog svojstva da registri mogu sadržati proizvoljno velike brojeve.

Ovako definiran RAM-stroj nije baš efikasan, ali je Turing-ekvivalentan. Kodiranjem ulaznih k-torki možemo smatrati da RAM-stroj računa funkcije s N u N. Klasa svih takvih funkcija, izračunljivih pomoću RAM-stroja, jednaka je klasi Turing-izračunljivih funkcija. Skicirajmo dokaz.

Konstruirajmo TS koji na ulazu prima 〈(p, w)〉, gdje je p valjani RAM-program, a w njegov ulaz. Znamo da je dovoljno konačno mnogo registara, pa možemo zahtijevati da traženi TS ima po jednu traku za svaki registar. Na tim trakama nalaze se vrijednosti odgovarajućih registara, npr. u binarnom zapisu. Nadalje, stroju ćemo dodati traku za kôd programa i ulaza, traku za programsko brojilo, te barem jednu radnu traku. TS mora znati povećavati i smanjivati vrijednost na registarskoj traci za 1, postavljati programsko brojilo, pronaći instrukciju prema njezinoj adresi i dekodirati je. Sve to možemo ostvariti, pa postoji TS koji simulira RAM-stroj.

Obratno, dovoljno je pokazati da postoji RAM-program koji simulira univerzalni TS. Preciznije, na ulazu program prima kôd nekog Turingova stroja M i njegova ulaza w, te simulira rad stroja M na ulazu w. Ostat ćemo dužni čitatelju RAM-programe koji implementiraju cjelobrojnu aritmetiku; neke od njih može naći u paketu MaMa ili ih napisati sam. Osnovna je ideja uzeti trenutačnu konfiguraciju od M, dekodirati je, primijeniti funkciju prijelaza (ako je definirana, u suprotnom zavrtiti program u beskonačnoj petlji) i zakodirati novu konfiguraciju.

Ovim završavamo pregled apstraktnih strojeva i prelazimo na jedan "matematičkiji" model izračunavanja.

6. Parcijalno rekurzivne funkcije

U ovom poglavlju definirat ćemo klasu parcijalno rekurzivnih funkcija, navesti primjere i dokazati neka osnovna svojstva parcijalno rekurzivnih funkcija. Najvažnije svojstvo koje ćemo (u ovom poglavlju) dokazati je da su sve parcijalno rekurzivne funkcije RAM-izračunljive.

Nećemo promatrati samo funkcije čija je domena cijeli skup prirodnih brojeva N. Zato uvodimo nekoliko oznaka i naziva koji će nam olakšati rad s takvim, takozvanim parcijalnim funkcijama.

•	Za funkciju kažemo da je totalna ako joj je domena skup N.
•	Za funkciju kažemo da je parcijalna ako joj je domena pravi podskup od N.
•	Za x ∈ Nk i funkciju f : S ⊆ Nk → N  s  f(x)↑ označavamo da f nije definirana u x, tj. da x nije u domeni funkcije f. S f(x)↓ označavamo da je f definirana u x, tj. da se x nalazi u domeni funkcije f.
•	Neka su f i g k-mjesne funkcije. Kažemo da je f parcijalno jednako g, u oznaci f(x)  g(x) ili f  g, ako vrijedi: f(x)↓ ako i samo ako g(x)↓, te za svaki x za koji je f(x)↓ vrijedi f(x)=g(x).

Počinjemo s definicijom klase inicijalnih funkcija:

Istaknimo odmah da je svaka inicijalna funkcija RAM-izračunljiva. Tvrdnju dokazujemo navodeći RAM-programe (točnije, riječ je o makro-programima) koji izračunavaju pojedine funkcije. Na primjer, makro-program

izračunava funkciju sljedbenika. Slično se kratkim programima pokazuje RAM-izračunljivost ostalih inicijalnih funkcija.

Inicijalne funkcije su, na neki način, najjednostavnije funkcije za koje možemo reći da su intuitivno izračunljive. Sada ćemo opisati dva načina dobivanja "složenijih funkcija", ali tako da intuitivni osjećaj izračunljivosti ostane očuvan.

Neka je G n-mjesna, a H₁,…,H_n k-mjesne funkcije. Za k-mjesnu funkciju F definiranu s  F(x)  G(H₁(x),…,H_n(x)) kažemo da je definirana pomoću kompozicije.

Navedimo nekoliko primjera funkcija koje se mogu dobiti koristeći samo inicijalne funkcije i kompoziciju.

1. Funkcija N_k : N^k → N definirana s N_k(x₁,…,x_k) = 0 može se dobiti kompozicijom inicijalnih funkcija:  N_k(x₁,…,x_k) = Z(I_{k, 1}(x₁,...,x_n)).
   
   
2. Promotrimo funkciju C_{k, n} : N^k → N definiranu s C_{k, n}(x₁,…,x_k) = n. Uočimo da vrijedi  C_{k, 0} = N_k,  C_{k, n+1}(x) = Sc(C_{k, n}(x)). Iz principa matematičke indukcije slijedi da se do svake od funkcija C_{k, n} može doći počevši od inicijalnih funkcija i koristeći samo kompoziciju.
   
   
3. Primjer nekonstantne funkcije koja se može iz inicijalnih funkcija dobiti kompozicijom je f(x) = x + 2, koja se može prikazati kao f(x) = Sc(Sc(x)).

Uočimo da se primjenom kompozicije ne gubi RAM-izračunljivost. Točnije, ako su G, H₁,…,H_n RAM-izračunljive funkcije, tada je i funkcija dobivena njihovom kompozicijom također RAM-izračunljiva. Sljedeći makro-program dokazuje tu tvrdnju:

Koriste se makroi oblika R_j ← F(R₁, …, R_k) koji izračunavaju vrijednost RAM-izračunljive funkcije F i spremaju je u registar R_j. Iz inicijalnih funkcija koristeći samo kompoziciju ne može se doći npr. do zbrajanja i množenja. Zato uvodimo sljedeću definiciju:

Klasa RAM-izračunljivih funkcija također je zatvorena na primitivnu rekurziju. Neka je G totalna k-mjesna RAM-izračunljiva funkcija, a H totalna (k+2)-mjesna RAM-izračunljiva funkcija te neka je funkcija F definirana primitivnom rekurzijom:  F(0, x) = G(x),  F(y+1, x) = H(F(y, x), y, x). Tada je F također RAM-izračunljiva. Tvrdnju dokazujemo u slučaju k = 1 tako što ćemo dati makro-program koji izračunava funkciju F:

Koristeći kompoziciju i primitivnu rekurziju dolazimo do veće klase funkcija. Te funkcije zvat ćemo primitivno rekurzivnim funkcijama. Preciznije:

Dokazali smo da je klasa RAM-izračunljivih funkcija zatvorena na kompoziciju i primitivnu rekurziju, te sadrži sve inicijalne funkcije, pa je svaka primitivno rekurzivna funkcija RAM-izračunljiva. Navedimo sada neke primjere primitivno rekurzivnih funkcija.

1. Funkciju zbrajanja možemo definirati primitivnom rekurzijom na sljedeći način:  x + 0 = I_{1, 1}(x),  x + (y + 1) = Sc(x + y). Dakle, zbrajanje je primitivno rekurzivna funkcija.
   
   
2. Funkciju prethodnik definiramo s  pr(0) = 0,  pr(x + 1) = x.
   
   
3. Modificirano oduzimanje:  x  0 = x,  x (y + 1) = pr(x  y). Uočimo da za x ≥ y vrijedi x  y = x − y, dok je za x < y uvijek x  y = 0.
   
   
4. Signum:  sg(0) = 0,  sg(x + 1) = 1. Vrijedi sg(0) = 0 i sg(x) = 1 za x > 0.

Uočimo da su sve primitivno rekurzivne funkcije totalne. Postoje i parcijalne funkcije koje bismo htjeli zvati "izračunljivima", kao i totalne funkcije koje nisu primitivno rekurzivne, a također bismo ih htjeli zvati "izračunljivima". Primjer takve funkcije je Ackermannova funkcija. Stoga uvodimo sljedeće definicije.

Neka je f : S ⊆ N^k+1 → N funkcija. S μy(f(x, y)  0) označavamo k-mjesnu funkciju definiranu na sljedeći način. Za x ∈ N^k,  μy(f(x, y)  0) je najmanji z takav da za svaki y < z vrijedi f(x, y)↓ i f(x,z) = 0, ako takav z postoji. U suprotnom je μy(f(x, y) 0)↑ (funkcija nije definirana za taj x). Kažemo da je funkcija μy(f(x, y)  0) definirana pomoću μ-operatora.

Uočimo da je svaka primitivno rekurzivna funkcija rekurzivna, a samim time i parcijalno rekurzivna. Neka je f : S ⊆ N^k+1 → N RAM-izračunljiva funkcija. Sljedeći makro-program izračunava funkciju μy(f(x, y)  0):

Dakle, klasa RAM-izračunljivih funkcija je zatvorena na μ-operator. Time smo dokazali:

Svaka parcijalno rekurzivna funkcija je RAM-izračunljiva.

Navedimo sada nekoliko svojstava i primjera rekurzivnih funkcija i relacija koje će nam trebati u sljedećem poglavlju.

1. Ako su R i P (primitivno) rekurzivne relacije, tada su ¬R, R∧P, R∨P, R→P i R↔P također (primitivno) rekurzivne relacije.
   
   
2. Ako je R(x, y) (primitivno) rekurzivna relacija, tada su relacije dobivene ograničenom kvantifikacijom, tj. P(x, z) :⇔ ∀y<z R(x, y)  i  Q(x, z) :⇔ ∃y<z R(x, y), također (primitivno) rekurzivne.
   
   
3. Relacije  =,  <,  >,  ≤  i  ≥  su primitivno rekurzivne.
   
   
4. Neka je R rekurzivna relacija. Definiramo funkciju μyR(x, y) koja elementu x pridružuje najmanji z takav da je R(x, z) ako on postoji, a inače je μyR(x, y)↑. Ta je funkcija također parcijalno rekurzivna.

7. Ekvivalencija klasa RAM-izračunljivih i parcijalno rekurzivnih funkcija

U prošlom poglavlju dokazali smo da je svaka parcijalno rekurzivna funkcija RAM-izračunljiva. Cilj ovog poglavlja je ilustrirati dokaz obrata te tvrdnje. Da bismo to učinili, trebamo RAM-stroj, stanja u registrima i njegov rad zakodirati u prirodne brojeve.

Prisjetimo se kako smo u uvodu definirali kodiranje uređenih k-torki. Kôd konačnog niza prirodnih brojeva (x₀, x₁, …, x_k−1) definiramo s〈x₀, x₁,…,x_k−1〉= p₀^x₀+1 · p₁^x₁+1 ·…· p_k−1^x_k−1+1, pri čemu je p_i i-ti prosti broj, tj. p₀ = 2, p₁ = 3, p₃ = 5, … U eksponente smo stavili x_i + 1 (umjesto x_i, što se na prvi pogled čini prirodnijim), jer bi inače neki različiti nizovi imali jednake kodove, npr. (1,2,3) i (1,2,3,0). Dogovorno uzimamo da je kôd praznog niza 1.

Znamo da je potenciranje parcijalno rekurzivno. Da bismo dokazali da je kodiranje i dekodiranje parcijalno rekurzivno, treba dokazati da je preslikavanje i  p_i također parcijalno rekurzivno. U tu svrhu promotrimo relacije Div(x, y) ⇔ "x je djeljiv s y" i Pr(x) ⇔ "x je prost" te uočimo da su one rekurzivne: na primjer, Div(x, y) ⇔ y ≠ 0 ∧ (∃z ≤ x) (x = zy). Nadalje, vrijedi  p₀ = 2,   p_n+1 = μx(Pr(x) ∧ x > p_n).

Slično, funkcija exp(x, i) = "eksponent prostog broja p_i u rastavu broja x na proste faktore" je parcijalno rekurzivna, te za x =〈x₀, x₁,…,x_k−1〉 vrijedi x_i = exp(x, j)  1. Nadalje, duljinu niza (x₀, x₁,…,x_k−1) možemo iz njegova kôda x izračunati pomoću parcijalno rekurzivne funkcije lh(x) = μi(exp(x, i) = 0). Uvjet da je x kôd nekog konačnog niza, u oznaci Seq(x), također je rekurzivan i možemo ga izraziti s x ≠ 0 ∧ (∀i < x) ( Div(x, p_i) → i < lh(x) ).

Prijeđimo sada na kodiranje RAM-stroja. U petom poglavlju vidjeli smo kako instrukcijama pridružujemo kôdove. RAM-programu P čije instrukcije redom imaju kôdove y₀, y₁, …, y_n−1 pridružujemo kôd〈y₀, y₁, …, y_n−1〉. Lako je pokazati da su relacije Ins(x) ⇔ "x je kôd neke instrukcije RAM-programa"  i  Prog(x) ⇔ "x je kôd nekog RAM-programa" rekurzivne.

Rad RAM-stroja za program P i ulazne podatke x = (x₀, x₁, …, x_k−1) zvat ćemo P-izračunavanjem za x. Iz načina kodiranja vidimo da ako se registar R_i javlja u RAM-programu s kôdom e, onda je i < e. Za izračunavanje RAM-programa P s kodom e na ulaznim podacima x = (x₀, x₁, …, x_k−1) važni su samo registri R_i za i < e + k. Dodali smo k jer je moguće da imamo k ulaznih podataka, a da se u programu ne pojavljuju svi registri. Na primjer, program koji izračunava funkciju f : N^k → N,  f(x) = 0 može se napisati bez korištenja registara R₁, …, R_k. Za određeni korak rada stroja, označimo s q_i broj zapisan u registru R_i. Kôd registara u tom trenutku definiramo s〈q₀, q₁, …, q_s〉, gdje je s = e + k  1. Neka je r_i kôd registara nakon i-tog koraka rada stroja (i = 0 označava početno stanje). Ako P-izračunavanje za x stane nakon m koraka, broj r =〈r₀, r₁, …, r_m〉 nazivamo kôdom P-izračunavanja za x.

Neka je r kôd P-izračunavanja za x. Izlazni rezultat tog izračunavanja može se dobiti kao vrijednost funkcije U(r) = ((r)_s)₀, gdje je s = lh(r)  1. Funkcija U, koju nazivamo univerzalnom funkcijom, je parcijalno rekurzivna i totalna (ako za brojeve r koji nisu kôdovi izračunavanja stavimo U(r) = 0), dakle rekurzivna. Štoviše, može se pokazati da je U primitivno rekurzivna.

Za opis rada stroja trebaju nam još dvije funkcije, za koje se također može pokazati da su rekurzivne.

1. Funkcija Count : N³ → N definirana s Count(e, x, n) = "broj zapisan u programskom brojilu nakon izvršenja n-tog koraka P-izračunavanja za (x₀, x₁, …, x_k−1)", pri čemu je e kôd programa P  i  x =〈x₀, x₁, …,x_k−1〉.
   
   
2. Funkcija Reg : N⁴ → N definirana s Reg(i, e, x, n) = "broj zapisan u i-tom registru nakon izvršenja n-tog koraka P-izračunavanja za (x₀, x₁, …, x_k−1)", pri čemu je e kôd programa P  i  x =〈x₀, x₁, …,x_k−1〉.

Koristeći do sada definirane funkcije, možemo definirati (također rekurzivne) relacije koje će nam govoriti staje li neki program u određenom broju koraka i odgovara li određeni kôd P-izračunavanju za x.

1. Za prirodne brojeve e, x, n ∈ N definiramo Step(e, x, n)  ⇔  "P-izračunavanje za (x₀, x₁, …, x_k−1) završava nakon n koraka", pri čemu je e kôd programa P  i  x =〈x₀, x₁, …,x_k−1〉.
   
   
2. Za  k, e ∈ N,  (x₀, x₁, …, x_k−1) ∈ N^k  i  y ∈ N definiramo T_k(e, x₀, x₁, …, x_k−1, y) ⇔ "y je kôd P-izračunavanja za (x₀, x₁, …, x_k−1)", pri čemu je e kôd programa P.

Relacije T_k,  k ∈ N\{0} nazivamo Kleenejevim predikatima. Može se pokazati da su Kleenejevi predikati primitivno rekurzivne relacije. Sada smo spremni definirati funkciju iz koje će slijediti da je svaka RAM-izračunljiva funkcija parcijalno rekurzivna.

Neka su  e ∈ N,  k ∈ N  i  x ∈ N^k. Definiramo {e}_k(x) kao izlazni rezultat P-izračunavanja za x, ako je e kôd programa P i izračunavanje staje, a u suprotnom {e}_k(x)↑.

Neka je r kôd P-izračunavanja za (x₀, x₁, …, x_k−1) koje staje. Tada je izlazni rezultat jednak U(r) i vrijedi r = μyT_k(e, x₀, x₁, …, x_k−1, y). Dakle, {e}_k(x₀, x₁, …, x_k−1)  U(μyT_k(e, x₀, x₁, …, x_k−1, y)), tj. {e}_k je parcijalno rekurzivna funkcija.

Neka je f : S⊆N^k → N RAM-izračunljiva funkcija. Tada postoji RAM-program P koji je izračunava. Neka je e kod programa P. Tada za sve (x₀, …, x_k−1) ∈ N^k vrijedi:

f(x₀, x₁, …, x_k−1)    {e}_k(x₀, x₁, …, x_k−1)    U(μyT_k(e, x₀, x₁, …, x_k−1, y)).

Vidimo da je f parcijalno rekurzivna funkcija, što smo i željeli dokazati.

Kleenejev teorem o normalnoj formi za parcijalno rekurzivne funkcije.
Postoji primitivno rekurzivna funkcija U : N → N i primitivno rekurzivne relacije T_k ⊆ N^k+2,  k ∈ N\{0},  takve da za svaku k-mjesnu parcijalno rekurzivnu funkciju f postoji e ∈ N za koji je  f(x₀, x₁, …, x_k−1)  U(μyT_k(e, x₀, x₁, …, x_k−1, y)).

Funkcija U i relacije T_k koje se spominju u Kleenejevom teoremu upravo su ranije definirana univerzalna funkcija i Kleenejevi predikati.

Literatura

0. Uvod
1. Turingov stroj
2. Varijante Turingovih strojeva
3. Halting problem
4. Izračunljive funkcije i brojevi
5. RAM i makro-stroj
6. Parcijalno rekurzivne funkcije
7. Ekvivalencija klasa RAM-izračunljivih i parcijalno rekurzivnih funkcija
Literatura