Sadržaj:

1. Uvod
2. Primjeri riješenih zadataka
3. Zadaci za samostalan rad
Literatura

1. Uvod

Većinu problema iz oblasti euklidske geometrije moguće je rješiti upotrebom tzv. sintetičkih metoda. Međutim, ponekad traženje tog "elementarnog" rješenja predstavlja poteškoću i vrsnim poznavaocima geometrije, tako da su se stoljećima razvijale različite nesintetičke metode (analitička geometrija, kompleksni brojevi u geometriji, vektori), koje su olakšale rješavanje mnogih problema u ovom polju. Afine transformacije se nalaze negdje između sintetičkih i nesintetičkih metoda: ne pretvaraju geometrijski problem u algebarski (kao što to čine analitičke metode), ali su neodvojivo povezane sa vektorima, vektorskim prostorima i koordinatnim sistemima. U ovom tekstu ćemo pokušati da sistematično iznesemo teoriju afinih transformacija u ravni, prilagođenu srednjoškolskom nivou, te da kroz niz ilustrativnih primjera pokažemo njihovu primjenu pri rješavanju različitih geometrijskih problema.

Pomenimo još i da se svaka afina transformacija ravni može predstaviti u obliku

(x, y)  (ax + by + e, cx + dy + f)

za neke realne konstante a, b, c, d, e, f (zbog bijektivnosti potreban je i uslov ad − bc ≠ 0). Obično se transformacija prikazuje u formi matrice:

Više o matričnim transformacijama ravni možete saznati iz članka [BJ].

Sva izometrijska preslikavanja su afine transformacije. To je npr. očito za najpoznatije predstavnike izometrijskih preslikavanja: translaciju, rotaciju, osnu i centralnu simetriju. Slijedećih pet teorema predstavljaju teoretske osnove afinih transformacija. Napomenimo još i to da su teoreme 2, 4 i 5 osnovno "oružje" u primjeni ove metode u planimetriji, što ćete u nastavku i vidjeti na primjerima.

Na ovom mjestu bilo bi korisno ponoviti osnovne činjenice o vektorskom prostoru V², tj. o vektorskoj ravni. Njezini elementi su vektori – klase međusobno ekvivalentnih orijentiranih dužina. Orijentirane dužine AB i CD su ekvivalentne (tj. predstavljaju isti vektor) ako dužine AD i BC imaju isto polovište. Poznato je da iz svake tačke ravni možemo "nanijeti" bilo koji vektor. Vektore sabiramo po "pravilu trougla": AB + BC = AC. Za više informacija o vektorskoj algebri i teoriji vektorskih prostora, pogledati [MM].

Afina transformacija ravni L na prirodan način prenosi se i na vektore: L(AB) = L(A)L(B). Pokažimo najprije da je ova definicija dobra, tj. da ne ovisi o izboru predstavnika vektora.

Lema 1.  Neka su A₁, B₁, C₁, D₁ slike tačaka A, B, C, D, redom, preslikanih afinom transformacijom L. Ako je AB = CD, tada je A₁B₁ = C₁D₁.

Dokaz.  Neka je AB = CD. U slučaju da tačke A, B, C i D nisu kolinearne, ABCD je paralelogram. Kako se paralelne prave slikaju u paralelne prave (što ćemo dokazati u teoremi 2(c)), to je i A₁B₁C₁D₁ također paralelogram, pa je A₁B₁ = C₁D₁. Ukoliko su tačke A, B, C, D kolinearne, uzmimo tačke E i F koje nisu kolinearne sa njima tako da je EF = AB. Tada je A₁B₁ = E₁F₁ = C₁D₁.  □

Teorema 1.  Ako je L afina transformacija, tada vrijedi

• (a)  L( 0 ) = 0,
• (b)  L( a + b ) = L( a ) + L( b ) za proizvoljne vektore a , b iz V²,
• (c)  L(ka ) = k L( a ) za proizvoljan vektor a i realan broj k.

Dokaz.  (a)  L( 0 ) = L( AA ) = L( A )L( A ) = 0 .
(b)  Neka je a = AB i b = BC. Koristeći definicije sabiranja vektora i djelovanja afine transformacije na vektore dobijamo L( AB + BC ) = L( AC ) = L(A)L(C) = L(A)L(B) + L(B)L(C) = L( AB ) + L( BC ).
(c)  Uzmimo prvo da je k cio broj. Tada za prirodno k vrijedi L(k a ) = L( a + … + a ) = L( a ) + … + L( a ) = k L( a ), a za negativno k dovoljno je u prethodnom izrazu iskoristiti k a = (−k)(−a ). Sada, neka je k = m⁄n racionalan broj; n L(k a ) = L(n k a ) = L(m a ) = m L( a ), pa je L(k a ) = (m⁄n)L( a ) = k L( a ). Konačno, ako je k iracionalan broj, postoji niz k_n racionalnih brojeva koji teže ka k (npr. niz decimalnih aproksimacija broja k). Kako je L neprekidna funkcija, L(k a ) = L( n→∞ lim k_n a ) = n→∞ lim k_nL( a ) = k L( a ). □

Teorema 2.  Afine transformacije čuvaju:

• (a)  kolinearnost tačaka,
• (b)  konkurentnost pravih,
• (c)  paralelnost pravih,
• (d)  omjer dužina na pravcu,
• (e)  omjer površina poligona.

Dokaz.  (a)  Slijedi direktno iz činjenice da se afinom transformacijom prava slika u pravu.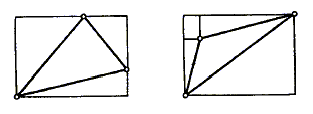
(b)  Slijedi iz činjenice da se prava slika u pravu i da je u pitanju bijekcija, jer se tada slika tačke presjeka pravih koje se preslikavaju nalazi u presjeku slika svake od tih pravih.
(c)  Analogno dokazu (b), iz činjenice preslikavanja prave u pravu i bijektivnosti, slike pravih koje se ne sijeku se također ne sijeku.
(d)  Neka je L afina transformacija i neka tačka C dijeli duž AB u omjeru p : q. Pokažimo da tada i C' dijeli duž A'B' u istom omjeru, pri čemu je L(A) = A', L(B) = B' i L(C) = C'. Zbog teoreme 1, iz uslova q AC = p CB slijedi q A'C' = q L( AC ) = L(q AC) = L(p CB) = p L( CB) = p C'B'.
(e)  Neka su a₁ i a₂ dvije okomite prave. Pošto afina transformacija čuva omjer dužina na paralelnim pravima, dužine svih duži paralelnih jednoj pravoj se množe istim koeficijentom. Označimo sa k₁ i k₂ ove koeficijente za prave a₁ i a₂ redom, i neka je ψ ugao između slika ovih pravih. Pokažimo da data afina transformacija množi površine svih poligona sa k, gdje je k = k₁ k₂ sin ψ. Za pravougaonike stranica paralelnih sa a₁ i a₂ i za pravougli trougao kateta paralelnih sa a₁ i a₂ tvrđenje očito vrijedi. Bilo koji drugi trougao može se dobiti isjecanjem nekoliko takvih pravouglih trouglova iz pravougaonika stranica paralenih sa a₁ i a₂ (slika 1). Dakle, tvrdnja važi za svaki trougao, pa samim tim i za svaki poligon (jer je svaki poligon moguće nepresjecajućim dijagonalama izdjeliti na trouglove). □

Slika 1.

Na ovom mjestu vrijedi primjetiti da afine transformacije općenito ne čuvaju udaljenost između tačaka niti uglove. To se jednostavno pokazuje na primjeru transformacije istezanja, definisane kao (x, y) → (cx, y) za realnu konstantu c ≠ 0. Ovim ograničenjima je umnogome određen i tip problema u kojima se efikasno mogu primjeniti afine transformacije. Tako, zbog teoreme 2, vidljivo je da su ove transformacije izuzetno korisne pri radu sa omjerima, kao dužinskim tako i površinskim (što će se vidjeti na primjerima), te sa konkurentnim i paralelnim pravima. S druge strane, zbog svojih ograničenja, afine transformacije su izuzetno nepraktične u problemima u kojima se javljaju dužine duži (bez omjera) i uglovi, pa samim tim normale, konciklične tačke i slično.

Teorema 3.  Neka su zadane dvije tačke u ravni, O i O', i dvije baze vektorskog prostora V ², {e₁, e₂} i {e'₁, e'₂}. Tada postoji jedinstvena afina transformacija koja preslikava O u O' i {e₁, e₂} u {e'₁, e'₂}.

Dokaz.  Definišimo preslikavanje L na slijedeći način. Neka je X proizvoljna tačka. Pošto je { e₁, e₂ } baza vektorskog prostora, onda postoje jedinstveni brojevi x₁ i x₂ takvi da je OX = x₁e₁ + x₂e₂ . Pridružimo tački X tačku X' = L(X) takvu da je O'X' = x₁e'₁ + x₂e'₂ . Kako je { e'₁, e'₂ } također baza, konstruisano preslikavanje je bijekcija (inverzno preslikavanje se da konstruisati na sličan način), a pokazuje se i da je neprekidno. Dokažimo sada da je slika bilo koje prave AB po preslikavanju L također prava. Neka je A' = L(A), B' = L(B) i neka su (a₁, a₂) i (b₁, b₂) koordinate tačaka A i B, redom, u bazi { e₁, e₂ } (tj. OA = a₁e₁ + a₂e₂, OB = b₁e₁ + b₂e₂ ). Uzmimo proizvoljnu tačku C na pravoj AB. Kako vrijedi AC = kAB za neko k, to je OC = OA + AC = OA + k AB = OA + k( OB − OA ) = (1 − k)OA + kOB = ((1 − k)a₁ + kb₁)e₁ + ((1 − k)a₂ + kb₂)e₂. Po definiciji preslikavanja L, za sliku C' = L(C) vrijedi O'C' = ((1 − k)a₁ + kb₁)e'₁ + ((1 − k)a₂ + kb₂)e'₂ = (1 − k)O'A' + kO'B' = O'A' + k( O'B' − O'A' ) = (1 − k) O'A' + k A'B' pa tačka C' leži na pravoj A'B'. Jedinstvenost preslikavanja L slijedi iz teoreme 1. Zaista, L( OX ) = x₁L( e₁ ) + x₂L( e₂ ), dakle, slika tačke X jednoznačno je određena slikama vektora e₁ i e₂ i slikom tačke O.  □

Teorema 4.  Za data dva trougla ABC i A₁B₁C₁ postoji jedinstvena afina transformacija koja jedan preslikava u drugi.

Dokaz.  Dovoljno je u teoremi 3 uzeti O = A, e₁ = AB, e₂ = AC, O' = A₁, e'₁ = A₁B₁, e₂ = A₁C₁.  □

Iz teoreme 4 i teoreme 2(c) slijedi

Teorema 5.  Za data dva paralelograma postoji jedinstvena afina transformacija koja jedan preslikava u drugi.

2. Primjeri riješenih zadataka

Zahvaljujući teoremama 4 i 5, često pri rješavanju problema u proizvoljnom trouglu možemo problem svesti na dokazivanje tvrdnje u jednakostraničnom trouglu, što je često mnogo lakše. Slično, paralelogram je moguće (po potrebi) transformisati u kvadrat. Ponekad je, pak, praktičnije trougao zamijeniti jednakokrakim trouglom, što ćemo vidjeti na nekim od primjera što slijede. Naravno, pri svakoj od transformacija mora se paziti na zakonitosti iz teoreme 2 i ograničenja vezana za uglove i dužine.

Na slijedećih nekoliko primjera vidjećemo iz prve ruke afine transformacije "na djelu". Biće tu i relativno lahkih i teških problema (tu je i jedan prijedlog za IMO). Zadaci su izabrani tako da pokažu standardni metod rješavanja planimetrijskih problema uz pomoć afinih transformacija i omoguće zainteresiranom čitaocu da riješi probleme za samostalan rad na kraju članka, te da lahko prepozna mogućnost primjene afinih transformacija u problemima sa kojim se bude u budućnosti susretao (na takmičenjima, u nastavi ili istraživačkom radu).

Primjer 1. ([IJ])  Po dvije prave su povučene kroz svako tjeme trougla tako da naspramnu stranicu dijele na tri jednaka dijela. Dokažite da se dijagonale koje spajaju naspramna tjemena šestougla nastalog u presjeku ovih pravih sijeku u jednoj tački.

Rješenje.  U zadatku su očito "u igri" samo omjeri na pravima i konkurentnost, osobine koje afina tranformacija čuva (prema teoremi 2). U skladu sa teoremom 4, možemo dati trougao transformisati u jednakostranični i u njemu dokazati tvrđenje zadatka. Neka tačke A₁, A₂, B₁, B₂, C₁, C₂ dijele stranice jednakostraničnog trougla ABC na jednake dijelove i neka su A', B', C' središta stranica (slika 2). Kako su prave BB₁ i CC₂, te BB₂ i CC₁ simetrične u odnosu na pravu AA', a simetrične prave se sijeku na osi simetrije, to se jedna dijagonala razmatranog šestougla nalazi na AA'. Slično, preostale dijagonale se nalaze na BB' i CC'. Jasno je, dalje, da se težišnice AA', BB', CC' sijeku u jednoj tački, čime je tvrdnja dokazana.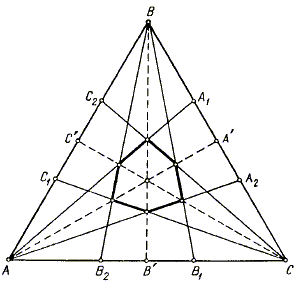

Slika 2.

Primjer 2. ([VP])  Na stanicama AB, BC, CD, DA paralelograma ABCD izabrane su redom tačke A₁, B₁, C₁, D₁, a na stranicama A₁B₁, B₁C₁, C₁D₁, D₁A₁ četverougla A₁B₁C₁D₁ izabrane su redom tačke A₂, B₂, C₂, D₂ tako da vrijedi

Dokažite da je A₂B₂C₂D₂ paralelogram čije su stranice paralelne sa stranicama paralelograma ABCD.

Rješenje.  Prema teoremi 5, svaki paralelogram se može afinom transformacijom transformisati u kvadrat. Dovoljno je trougao ABC transformisati u jednakokrako-pravougli trougao i paralelogram ABCD postaje kvadrat. Pošto su osnovni elementi u problemu omjeri dužina na pravoj i paralelne prave, to ovdje možemo primjeniti afine transformacije i uzeti u daljem razmatranju da je ABCD kvadrat.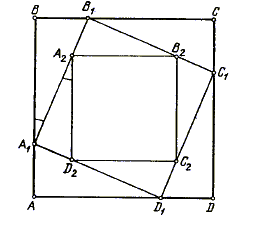

Slika 3.

Razmotrimo rotaciju za ugao od 90° oko središta kvadrata ABCD koja ga preslikava u samog sebe. Ovom rotacijom se i četverouglovi A₁B₁C₁D₁ i A₂B₂C₂D₂ slikaju sami u sebe. Prema tome, i oni su kvadrati (pokažite to!) pa vrijedi |AA₁| = |BB₁|, |B₁A₂| = |A₁D₂| i dovoljno dokazati da je npr. AB ‖ A₂D₂. Imamo:

Iz toga slijedi AB ‖ A₂D₂, što smo i htjeli pokazati.

Primjer 3. ([VP])  U trapezu ABCD osnovica AB i CD, kroz tačku D povučena je prava paralelna sa krakom BC, koja siječe dijagonalu AC u tački P. Prava paralelna sa krakom AD, povučena kroz tačku C, siječe dijagonalu BD u tački Q. Dokažite da je prava PQ paralelna sa osnovicama trapeza ABCD.

Rješenje.  Neka je E sjecište dijagonala trapeza. Afina transformacija koja trougao ADE preslikava u jednakokraki trougao preslikava trapez ABCD u jednakokraki trapez A'B'C'D'. Tada su tačke P' i Q' simetrične u odnosu na simetralu duži A'B', pa je P'Q' ‖ A'B'.

Primjer 4. ([IJ])  Neka je tačka T težište trougla ABC i neka su M, N, P tačke na stranicama AB, BC, CA trougla, redom, koje dijele ove stranice u istom omjeru (|AM| : |MB| = |BN| : |NC| = |CP| : |PA| = p : q). Dokažite:

  (a) T je težište trougla MNP,

  (b) T je težište trougla čija su tjemena u presjeku pravih AN, BP i CM.

Rješenje.  (a) Afinom transformacijom preslikajmo trougao ABC u jednakostranični trougao A'B'C'. Neka su T', M', N', P' slike tačaka T, M, N, P. Rotacijom za ugao od 120° oko tačke T' trougao M'N'P' se slika u samog sebe. Prema tome, to jednakostranični trougao, a T' mu je težište, odnosno sjecište težišnica. Pošto se afinom transformacijom težišnica slika u težišnicu, T je težište trougla MNP.
(b) Na isti način zaključujemo da je T težište i trougla nastalog u presjeku pravih AN, BP i CM.

Primjer 5. ([JS])  Za svaki skup S od pet tačaka u ravni od kojih nikoje tri nisu kolinearne, sa M(S) i m(S) označene su najveća i najmanja površina trouglova određenih tačkama iz S. Koja je najmanja moguća vrijednost omjera M(S)/m(S)?

Rješenje.  Dokažimo da je najmanji mogući omjer (1+√5)/2 i da se on postiže ako se S sastoji od vrhova pravilnog petougla. Označimo sa A, B, C, D i E tačke skupa S i neka je P(∆ABC) = M(S). Neka je k = 2M(S)/(1 + √5). Sada trebamo pokazati da barem jedan od trouglova formiranih od tačaka iz skupa S ima površinu manju ili jednaku k. Povucimo pravce B'C', C'A' i A'B' kroz A, B, C paralelne sa BC, CA, AB redom (slika 4).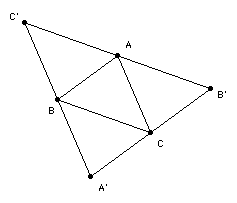

Slika 4.

Tačka D se mora nalaziti na istoj strani prave B'C' kao i BC, inače bi vrijedilo P(∆BCD) > P(∆ABC), što se protivi činjenici da je P(∆ABC) maksimalna. Slično, D se nalazi sa iste strane C'A' kao i CA, te sa iste strane A'B' kao i AB. Prema tome, D se nalazi ili unutar ∆ABC ili na jednoj od njegovih stranica. Slično zaključujemo i za tačku E. Kako su trouglovi A'BC, B'CA, C'BA disjunktni (izuzimajući tačke A, B i C, u kojima se tačke D i E ne mogu naći), u jednom od njih se ne nalazi ni D ni E. Bez umanjenja općenitosti, uzmimo da se tačke D i E nalaze u četverouglu B'CBC'.

Afine transformacije čuvaju omjer površina trouglova; zato možemo transformisati ∆ABC u trougao uglova 36°, 72°, 72° što će nam omogućiti da odaberemo tačke P i Q tako da je APBCQ pravilan petougao. Pošto je AB ‖ CQ i AB ‖ A'B', tačka Q se nalazi na pravcu B'C. Analogno, P se nalazi na BC'.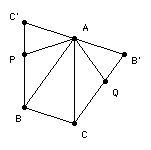

Slika 5.

Sada razmotrimo dva slučaja, u zavisnosti da li se tačke D i E nalaze unutar ili van petougla APBCQ.

1. Tačka D se nalazi u petouglu. Ako se nalazi u ∆ABP, tada je P(∆ABD) ≤ P(∆ABP) = k. Slično vrijedi i ako se D nalazi u ∆ACQ. Ako se pak nalazi u ∆ABC, tad je površina bar jednog od trouglova ∆ABD, ∆BCD, ∆CAD manja ili jednaka od P(∆ABC)/3 < k. Slično zaključujemo i za tačku E.

2. Tačke D i E se nalaze u ∆APC' ili ∆AQB'. Ako se obje nalaze u istom trouglu, tada je P(∆ADE) ≤ P(∆APC') < k. Ako se nalaze u različitim trouglovima, na primjer D u ∆APC' i E u ∆AQB', tada je P(∆ADE) = (|AD| · |AE|/2) sin∠DAE ≤ (|AP|²/2) sin∠PAQ = P(∆PAQ) = k.

Analizom navedenih primjera mogli ste vidjeti uobičajene ideje, metode i tehnike vezane za rad sa afinim transformacijama, ali i primjere nestandardnih ideja koje zahtjevaju izvjesnu dozu imaginacije i kreativnosti. Ideje iz ovih primjera pokušajte iskoristiti u zadacima za samostalan rad koji se nalaze na kraju teksta. Neki od njih se daju riješiti standardnim putem, no neki će zahtjevati od rješavača nove ideje. Neka vas ne obeshrabri početni neuspjeh u nekim od zadataka. Probajte opet, posmatrajte, razmišljajte, analizirajte!

3. Zadaci za samostalan rad

Zadatak 1. ([VP])  Na stranicama AB, BC i CD paralelograma ABCD su izabrane tačke K, L i M redom, tako da dijele stranice u istom omjeru. Neka su b, c i d prave koje prolaze tačkama B, C i D i paralelne su sa KL, KM, ML redom. Dokažite da se prave b, c i d sijeku u jednoj tački.

Zadatak 2. ([VP])  Na stranicama AB, BC i AC trougla ABC se nalaze tačke M, N i P redom. Dokažite:

(a) Ako su tačke M₁, N₁ i P₁ centralno simetrične tačkama M, N i P u odnosu na središta odgovarajućih stranica, tada je P(∆MNP) = P(∆M₁N₁P₁)

(b) Ako se tačke M₁, N₁ i P₁ nalaze na stranicama AC, BA i CB redom, tako da je MM₁ ‖ BC, NN₁ ‖ CA, PP₁ ‖ AB, tada je P(∆MNP) = P(∆M₁N₁P₁).

Zadatak 3. ([KK])  Neka su X, Y, Z tačke na stranicama BC, CA, AB, redom, trougla ABC za koje važi |BX| / |XC| = |CY| / |YA | = |AZ| / |ZB| = k, za zadanu konstantu k > 1. Pronadite odnos površina trougla čija se tjemena nalaze u presjeku duži AX, BY i CZ i trougla ABC (kao funkciju od k).

Zadatak 4. ([ML], Albanija 2004.)  Odrediti omjer površine osmougla koji se nalazi u presjeku pravih povučenih iz tjemena paralelograma do središta naspramnih stranica s površinom tog paralelograma.

Zadatak 5. ([MR], Švedska 1996.) Kroz tačku u unutrašnjosti trougla površine T povučene su prave paralelne stranicama trougla, koje ga dijele na tri trougla i tri paralelograma. Neka su T₁, T₂, T₃ površine dobijenih trouglova. Dokažite da je √T = √T₁ + √T₂ + √T₃.

Zadatak 6. ([DJ], prijedlog za IMO 1995.) Neka je O tačka u unutrašnjosti konveksnog četverougla ABCD, čija je površina S i neka su K, L, M i N tačke na stranicama AB, BC, CD i DA, redom. Ako su OKBL i OMDN paralelogrami, dokazati da je √S ≥ √S₁ + √S₂, gdje su S₁ i S₂ redom površine četverouglova ONAK i OLCM.

Slijedeći zadatak naveden je pogrešno u [KK] i [MR]. Ovdje je dat ispravljen tekst.

Zadatak 7.  Neka je ABCDE konveksan petougao i neka je F = BC ∩ DE, G = CD ∩ EA, H = DE ∩ AB, I = EA ∩ BC, J = AB ∩ DC. Ukoliko je P(∆AHI) = P(∆BIJ) = P(∆CJF) = P(∆DFG) = P(∆EGH), dokažite da se prave AF, BG, CH, DI, EJ sijeku u jednoj tački.

Literatura

1. Uvod
2. Primjeri riješenih zadataka
3. Zadaci za samostalan rad
Literatura