Hrvatski matematički elektronski časopis math.e

Broj 2 

















 

Matko Botinčan, Dubravko Lapaine, Rudolf Markulin, Ana Žgaljić

Vibracije mehaničkih sustava

Teorija | Primjeri | Download | Linkovi | Dno stranice | Verzija za printanje

Teorija

KRATKA (STVARNO KRATKA) POVIJEST PROUČAVANJA VIBRACIJA

Ljudi su se počeli zanimati za vibracije već od pojave prvih muzičkih instrumenata, vjerojatno bubnjeva i zviždaljki. Iako su već tada opažena stroga pravila, to još ne možemo zvati znanošću. Grčki filozof i matematičar Pitagora (582-507 pr.K.) smatra se prvim koji je na znanstvenoj osnovi promatrao zvukove i glazbu. Poznata su njegova promatranja ovisnosti duljine i napetosti žice i visine tona koji se proizvodi. Od njegovih istraživanja ništa nije ostalo zapisano. Galileo Galilei (1564-1642) smatra se osnivačem moderne eksperimentalne znanosti. Proučavao je jednostavna njihala jedne crkve u Pisi. Jednog dana, jer mu je propovijed bila dosadna, Galileo se zagledao u strop. Njišuća svjetiljka zaokupila je njegovu pažnju i mjerenjima njenih kretanja ustanovio je, na svoje zaprepaštenje, da je period njihanja neovisan o amplitudi kojom se njihalo njiše. Galileo je ostavio dva pisana djela i od tad su se stvari počele znatno brže razvijati. Od poznatih matematičara i fizičara koji su se bavili problemom vibracija tu su još i: Sir Isaac Newton (1642-1727), Brook Taylor (1685-1731), Daniel Bernoulli (1700-1782), Jean D'Alembert (1717-1783), Leonard Euler (1707-1783), Simeon Poisson (1781-1840), G. R. Kirchoff (1842-1887)...pa sve do suvremenih.

VAŽNOST PROUČAVANJA VIBRACIJA

Većina ljudskih aktivnosti uključuje vibracije u jednom od njezinih pojavnih oblika. Primjerice: čujemo jer se vibracije prenose preko naših bubnjića, disanje je povezano s vibracijom naših pluća, hodanje uključuje (periodičke) oscilacije naših ruku i nogu, a govorimo zahvaljujući vibriranju naših glasnica.

Većina vozila ima vibracijskih problema zbog neuravnoteženosti motora. Na primjer, neuravnoteženost diesel motora može proizvesti potresne valove dovoljno jake da budu smetnja u urbanim zonama. Kotači lokomotiva se pri velikim brzinama zbog neuravnoteženosti mogu odvojiti više od centimetra od tračnica. U turbinama vibracije uzrokuju spektakularne mehaničke kvarove. Općenito, vibracije rezultiraju bržim trošenjem i kvarovima dijelova motora kao što su nosači i kotači, a također stvaraju i jaku buku.

Kad god se prirodna frekvencija vibracije motora ili strukture podudara s frekvencijom vanjskog poticaja, nastaje fenomen koji se zove rezonancija. Ona dovodi do iznimnih odstupanja i kvarova. Literatura je puna primjera razornog djelovanja rezonancija (vidi filmić razrušenog mosta tacoma.mpeg). Zbog devastirajućeg efekta kojeg vibracije imaju na strojeve i strukture, testiranje na vibracije postalo je standardan postupak u dizajnu i razvoju većine inženjerskih sustava.

Usprkos svojim štetnim efektima, vibracije se mogu uspješno iskoristiti u nekoliko potrošačkih i industrijskih primjena. Štoviše, primjena vibracijske opreme proteklih se godina znatno povećala. Na primjer, vibracije su iskorištene u vibracijskim tekućim vrpcama, sijačima, sitima, perilicama rublja, električnim četkicama za zube, zubarskim bušilicama, satovima i električnim masažnim uređajima. Vibracije se koriste za simulacije potresa radi geoloških istraživanja i pri istraživanjima dizajna nuklearnih reaktora.

OSNOVNI KONCEPTI VIBRACIJA

Svako gibanje koje se ponavlja u nekom vremenskom intervalu zove se vibracija ili oscilacija. Gibanje njihala je tipičan primjer vibracija.

Vibracije u sustavu uključuju prijenos potencijalne energije u kinetičku i obrnuto. Ako je sustav prigušen, energija se gubi u svakom ciklusu.

Stupnjevi slobode: minimalni broj nezavisnih koordinata potrebnih da se u potpunosti odredi pozicija svih dijelova sustava u svakom trenutku vremena definira stupnjeve slobode. Jednostavno njihalo (kao na slici) predstavlja sustav s jednim sustavom slobode. Na primjer, gibanje njihala može se predstaviti u terminima kuta $\theta$ ili u terminima Kartezijevih koordinata $x$ i $y$. Ako se koordinate $x$ i $y$ uzmu za opisivanje gibanja, mora se uočiti da te koordinate nisu nezavisne. Povezane su, zbog konstante duljine niti $l$, relacijom $x^2+y^2=l^2$. Stoga bilo koja od koordinata $x$ i $y$ može biti odabrana za opisivanje gibanja njihala. Mi ćemo se ovdje baviti sustavima s jednim stupnjem slobode.

MATEMATIČKA NADOPUNA (derivacija)

U ovom ćemo poglavlju probati "na prste" objasniti derivacije. Nećemo zalaziti u stroge matematičke definicije, nego ćemo im pristupiti tako da steknemo što bolji osjećaj o tome što su i kako nam derivacije koriste za rješavanje naših problema. Neka je dana funkcija $f$, te neka je to realna funkcija realne varijable ( $f: {\mathbb{R}}\rightarrow {\mathbb{R}}$). Derivacija funkcije $f$ u nekoj točki $c\in {\mathbb{R}}$ (ova oznaka znači da je $c$ neki realan broj) definira se kao

\begin{displaymath} f'(c)=\lim_{x\rightarrow c}\frac{f(x)-f(c)}{x-c}. \end{displaymath}

To zapravo znači da je derivacija funkcije $f$ u točki $c$ realan broj $f'(c)$ oko kojega se nakupljaju vrijednosti $\frac{f(x)-f(c)}{x-c}$ za neki izbor $x$-ova koji su "dovoljno" blizu $c$. Znači, nakupljaju li se $x$-evi oko $c$, vrijednosti $\frac{f(x)-f(c)}{x-c}$ nakupljat će se oko $f'(c)$.

Sada kada znamo što je to derivacija funkcije $f$ u točki, možemo vidjeti što je to derivacija funkcije.

Derivacija funkcije je funkcija definirana na istoj domeni (${\mathbb{R}}$) koja svakoj točki pridružuje derivaciju u točki te funkcije i označavamo je s $f'$. Gotovo sve funkcije koje svakodnevno koristimo su derivabilne (imaju derivaciju) i njihove su nam derivacije poznate. Za one druge funkcije, koje nemaju derivaciju (ima i takvih!), kažemo da nisu derivabilne. Za njih ne vrijedi ono "nakupljanje". Npr. $(x^2)'=2x$. Sve derivacije važnijih funkcija mogu se pronaći u bilo kojim matematičkim tablicama.

Analogno se definira $f''$ tj. druga derivacija funkcije $f$, ili derivacija funkcije $f'$, te sve derivacije višeg reda.

Pokušajmo vidjeti što je to derivacija u fizikalnom smislu. Zamislimo da imamo neko vozilo koje u vremenu $t$ prijeđe put $x$. Dakle, položaj tog vozila u bilo kojem trenutku dan je nekom funkcijom ovisnom o $t$. Recimo za $2 s$ vozilo će prijeći put $x(2).$ Npr. ako se radi o jednolikom gibanju, funkcija $x$ bila bi oblika

\begin{displaymath} x=\nu t+q, \end{displaymath} (1)

gdje je $\nu$ neki realan broj.

(Kako znamo da ona izgleda baš tako? Jednoliko gibanje je ono gibanje kod kojega je u jednakim vremenskim razmacima prijeđen jednak put, tj. funkcija $x$ mora zadovoljavati $x(t)-x(s)=x(a)-x(b)$ za $t-s=a-b$, a to očito zadovoljavaju funkcije oblika (1) i samo takve funkcije).

Za jednoliko gibanje derivacija bi bila

\begin{displaymath} \lim_{x\rightarrow c}\frac{\nu x - \nu c}{x-c} = \lim_{x\rightarrow c} \nu = \nu, \end{displaymath}

ali mi znamo da je kod jednolikog gibanja brzina konstantna i da je ona u nekom trenutku $t$, nakon prijeđenog puta $x(t)$, baš jednaka $\nu=\frac{x(t)}{t}$, pa je, dakle, derivacija ovakve funkcije $x$ baš brzina, tj. derivacija funkcije $x$ u trenutku (točki) $t$ je baš brzina u trenutku (točki $t$). Na ovom primjeru vidjeli smo fizikalno značenje derivacije. Dakle, derivacija je zapravo brzina. Analogno se može pokazati da je akceleracija druga derivacija, tj. ako je gibanje tijela dano nekom funkcijom $x(t)$, akceleracija tog tijela bit će $x''(t)$.

Diferencijalnom jednadžbom zvat ćemo onu jednadžbu u kojoj se pojavljuje derivacija neke funkcije, odnosno nešto ovakvog oblika:

\begin{displaymath} u'(t)=f(t, u(t)) \end{displaymath} (2)

To bi bila diferencijalna jednadžba prvog reda zato jer se funkcija $u$ pojavljuje s najviše prvom derivacijom. O tome kakva je funkcija $f$ nećemo se previše brinuti. Recimo samo da će sve funkcije $f$ koje će se nama pojaviti biti "dobre".

Rješenjem takve diferencijalne jednadžbe, nazovimo ga $u(t)$, zvat ćemo funkciju koja zadovoljava (2), tj. da uvrštavanjem $u(t)$ u (2) zaista dobijemo jednakost.

Sada kad "znamo" što je derivacija, pokušajmo predočiti što je integral. Integral, označavamo ga s $\int$, bila bi "obrnuta derivacija", odnosno integral funkcije $f'$ bila bi sama funkcija $f$. Npr. $\int (2x) = x^2$.

MATEMATIČKO NJIHALO

Zamislimo matematičko njihalo kao kuglicu mase $m$ obješenu o nit duljine $l$. Nit je "idealna", tj. smatramo da je nerastezljiva i da nema masu. Kuglicu ne promatramo u klasičnom smislu, nego kao masu koncentriranu u jednoj točki. Ako kuglicu pomaknemo iz položaja ravnoteže i pustimo, ona se zanjiše i njezino gibanje dano je jednadžbom

\begin{displaymath} \theta'' +\frac{g}{l}\sin{\theta}=0, \end{displaymath}

gdje je $\theta$ kao na slici. Znamo da je za $\theta$ dovoljno mali $\sin{\theta}\approx \theta,$ pa u slučaju ako promatramo titranje njihala oko položaja ravnoteže, dobivamo jednadžbu gibanja za male oscilacije:

\begin{displaymath} \theta'' +\frac{g}{l}\theta=0. \end{displaymath}

Primjer:

OPRUGA

Opruga je tijelo napravljeno od žice savijene u helikoidu (krivulja koja opisuje izgled opruge). Zamišljamo da je broj navoja velik i da je ona izdužena, tj. da je poprečni presjek malen u odnosu na duljinu. Sila opruge ima smjer prema nutrini opruge i iznosa je

\begin{displaymath} F=k x. \end{displaymath}

Konstanta opruge $k$ ovisi o materijalu opruge, radijusu namotaja $R$, broju namotaja $n$ i radijusu žice $r$. Točnije, $k$ je dan izrazom $k=\frac{\mu r^4}{4 n R^3}$, gdje je $\mu$ karakteristika materijala opruge. Pogledajmo kako se ponašaju dvije opruge spojene serijski odnosno paralelno. U oba slučaja želimo zamijeniti dvije opruge jednom tako da za danu oprugu odaberemo dobar $k$. Neka je $k_1$ konstanta prve opruge, a $k_2$ konstanta druge opruge.

U slučaju serijskog spoja imamo:

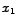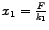  • opruga1 produlji se za $x_1$, $x_1=\frac{F}{k_1}$,
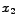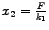  • opruga2 produlji se za $x_2$, $x_2=\frac{F}{k_1}$.

Zamijenimo ih jednom oprugom koja se produlji za $\frac{F}{k}$, pa sada imamo

\begin{displaymath} \frac{F}{k_1}+\frac{F}{k_2}= \frac{F}{k}, \end{displaymath}

tj.

\begin{displaymath} k=\frac{1}{\frac{1}{k_1}+\frac{1}{k_2}}. \end{displaymath}

Serijski spojene opruge ponašaju se kao paralelno spojeni otpornici.

Za slučaj paralelnog spoja opruga, na sličan način dobijemo da je $k$ opruge koja bi zamijenila dvije paralelno spojene opruge jednak zbroju njihovih konstanti, tj.

\begin{displaymath} k=k_1+k_2. \end{displaymath}

Primjer:

ELASTIČNI ŠTAP

Pretpostavimo da imamo homogeni elastični štap (npr. velika gumica za brisanje). Neka štap u blizini hvatišta uvijek ostaje okomit na ravninu hvatišta. Na kraj štapa stavimo masu $m$ ili djelujemo silom $F$. Neka je $u$ funkcija koja opisuje pomak u tom smjeru, tj. funkcija koja opisuje transverzalni pomak. Jednadžba ravnoteže za ovaj štap dana je kao

\begin{displaymath} E(Iu'')''=f, \end{displaymath}

gdje je $E$ Youngov modul elastičnosti, $I$ moment inercije presjeka štapa, $f$ linijska gustoća sile. Za ovakav štap se pokaze da vrijedi

\begin{displaymath} -(Eu'')'(l)=F. \end{displaymath}

Nadalje, uzimamo da je

\begin{displaymath} EIu''(l)=M \end{displaymath}

($M$ je moment uvijanja štapa), što se dobije integracijom prethodne jednadžbe. Uzmemo li da je $f=0$ (tj. štap nema mase) i $M=0,$ integracijom glavne jednadžbe dobivamo

\begin{displaymath} F=\frac{3EI}{l^3}u(l), \end{displaymath}

tj. ovime smo opet dobili jednadžbu za silu opruge, s time da je koeficijent opruge zamijenjen izrazom koji ovisi o svojstvima štapa.

Na sličan način, kad bismo promatrali longitudinalni pomak štapa dobili bismo izraz

\begin{displaymath} F=\frac{E A}{l} u(l), \end{displaymath}

gdje je $A$ površina presjeka, pa i u slučaju ovakvog gibanja, štap djeluje kao opruga.

Primjer:

SLOBODNE VIBRACIJE

Zamislimo masu $m$ obješenu na oprugu konstante $k$. Jednadžba gibanja mase $m$ dana je prema drugom Newtonovom zakonu kao

\begin{displaymath} m a=-k x. \end{displaymath}

Znamo da je akceleracija derivacija brzine pa je ona dana kao

\begin{displaymath} a=x''. \end{displaymath}

Stoga se jednadžba svodi na

\begin{displaymath} m x''=-k x. \end{displaymath}

Do iste jednadžbe dolazimo i primjenom zakona očuvanja energije.

Jednadžbu $mx''+kx=0$ rješavamo po $x$ i na taj način dobivamo funkciju $x(t)$ koja opisuje gibanje mase obješene na oprugu. Jednadžba se zapisuje u obliku

\begin{displaymath} x''+ \omega^2 x=0, \quad \mbox{ gdje je }\quad \omega=\sqrt{\frac{k}{m}}. \end{displaymath}

Opće rješenje ove jednadžbe dano je u obliku

\begin{displaymath} x(t)=A\cos{(\omega t)}+B\sin{(\omega t)}. \end{displaymath} (3)

Period ovog gibanja je $T=\frac{2 \pi}{\omega}$. $T$ ovisi samo o masi i konstanti opruge. Ako imamo zadan početni položaj mase $x(0)=x_0$ i početnu brzinu $x'(0)=x'_0$ lako se izračunaju konstante $A$ i $B$. Uvrštavanjem $0$ u (3) dobivamo $A= x_0$. Ako deriviramo (3), te nakon toga uvrstimo $0$ u dobivenu jednadžbu, dobivamo $B=\frac{x_0'}{\omega}$. Na taj način dobivamo rješenje u obliku

\begin{displaymath} x(t)=x_0\cos{(\omega t)}+\frac{x_0'}{\omega}\sin{(\omega t)}. \end{displaymath}

Primjedba. Ako za $A$ i $B$ uzmemo da je $A=\alpha \cos{\phi}$ i $B=\alpha \sin{\phi}$, za neke $\alpha$ i $\phi$ dobivamo da je $\alpha=\sqrt{A^2+B^2}=\sqrt{x_0^2+\frac{(x_0')^2}{\omega^2}}$ i $\mathop{\rm tg}\nolimits {\phi}=\frac{x_0'}{\omega x_0}=\frac{A}{B}$. U tom slučaju rješenje možemo zapisati u obliku

\begin{displaymath} x(t)= \sqrt{x_0^2+\frac{(x_0')^2}{\omega^2}}\cos{(\omega t-\phi)}. \end{displaymath}

Npr. graf jednog takvog rješenja izgleda ovako:

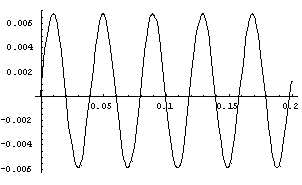
Image slika1

Primjer:

SLOBODNE VIBRACIJE S VISKOZNIM PRIGUŠENJEM

Jednadžba ovakvog sustava dana je kao

\begin{displaymath} m x''+F_{\rm prigusivaca} +k x=0. \end{displaymath}

$F_{\rm prigusivaca}$ ovisi o konstanti $c$ prigušivača i o brzini, tj. dana je izrazom $F_{\rm prigusivaca}=c x'$. Na taj način dobivamo jednadžbu

\begin{displaymath} m x''+c x'+k x=0. \end{displaymath} (4)

Da bi riješili ovu jednadžbu rješavamo pripadnu karakterističnu jednadžbu $m\lambda^2+c\lambda+k=0$. Dobivamo rješenja

\begin{displaymath} \lambda_{1, 2}=-\frac{c}{2m} \pm \frac{1}{2}\sqrt{\left(\frac{c}{m}\right)^2-4\frac{k}{m}}. \end{displaymath}

Opće rješenje jednadžbe (4) tada je dano kao

\begin{displaymath} x(t)=Ae^{\lambda_1 t}+Be^{\lambda_2 t}. \end{displaymath} (5)

Razlikujemo tri vrste rješenja:

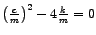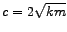  • 1. Slučaj. Vrijedi $\left(\frac{c}{m}\right)^2-4\frac{k}{m}=0$ tj. $c=2\sqrt{k m}$. S ovakvom konstantom prigušenja $c$ dobivamo KRITIČNO gušenje. U tom je slučaju rješenje dano izrazom

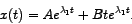
    \begin{displaymath} x(t)= Ae^{\lambda_1 t}+B t e^{\lambda_1 t}. \end{displaymath}

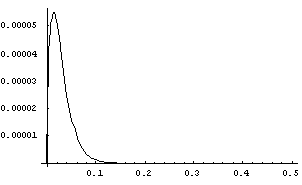
    Graf jednog ovakvog rješenja:

    Image slika2

    Primjer:

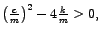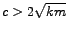  • 2. Slučaj. Vrijedi $\left(\frac{c}{m}\right)^2-4\frac{k}{m}>0,$ tj. $c>2\sqrt{k m}$. U ovom slučaju viskozno prigušenje veće je od kritičnog. Rješenje je dano u obliku (5), ali zbog ovakvog $c$ ovo rješenje ponovno trne. Ovakav slučaj zovemo VELIKO prigušenje.

    Graf jednog ovakvog rješenja:

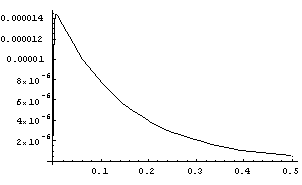
    Image slika3

    Primjer:

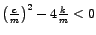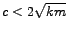  • 3. Slučaj. Vrijedi $\left(\frac{c}{m}\right)^2-4\frac{k}{m}<0$, tj. $c<2\sqrt{k m}$ . U ovom slučaju viskozno prigušenje manje je od kritičnog. Kako dobivamo kompleksna rješenja karakteristične jednadžbe, rješenje polazne jednadžbe dano je u obliku

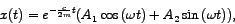
    \begin{displaymath} x(t)=e^{-\frac{c}{2m}t}(A_1\cos{(\omega t)}+A_2\sin{(\omega t)}), \end{displaymath}

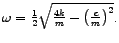    gdje je $\omega=\frac{1}{2}\sqrt{\frac{4k}{m}-\left(\frac{c}{m} \right)^2}.$ Ako uvedemo zamjenu 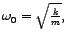$\omega_0=\sqrt{\frac{k}{m}},$ dobivamo $\omega=\omega_0 \sqrt{1-\frac{c^2}{4km}}$. Uočimo da je u ovom slučaju 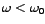$\omega<\omega_0$. Ovakav slučaj zovemo MALO prigušenje.

    Graf jednog ovakvog rješenja:

    Image slika4

    Primjer:

PRISILNE VIBRACIJE

Prisilne vibracije zbivaju se kada npr. na masu $m$ koja se nalazi obješena na opruzi konstante $k$ još djelujemo nekom silom $f$. U tom slučaju jednadžba za masu $m$ koja izlazi iz 2. Newtonovog zakona glasi

\begin{displaymath} mx''(t)+kx(t)=f(t). \end{displaymath} (6)

Uzimamo da je $f(t)=F\cos{(\Omega t)}$. Sada rješenje jednadžbe (6) tražimo u obliku $x(t)=x_h(t)+x_p(t),$ gdje je $x_h(t)=\alpha \cos(\omega_0 t- \phi)$ (pri čemu je $\omega_0=\sqrt{\frac{k}{m}}$ kružna frekvencija slobodnih oscilacija) rješenje homogene jednadžbe $m x''(t) + k x(t)=0$.

Partikularno rješenje tražimo u obliku $x_p(t) =A F \cos{(\Omega t)}$. Uvrštavanjem u (6) dobije se da je

\begin{displaymath} A=\frac{F}{k}\frac{1}{1-\frac{\Omega^2}{\omega_0^2}}. \end{displaymath}

Tu nastupa problem za $\Omega=\omega_0$. Taj slučaj razmotrit ćemo posebno.

Dakle, opće rješenje problema (6) dano je kao

\begin{displaymath} x (t)=\alpha \cos{(\omega_0 t-\phi)} + \frac{F}{k} \frac{1}{1-\frac{\Omega^2}{\omega_0^2}}\cos{(\Omega t)}. \end{displaymath}

Tu imamo superpoziciju dviju harmonijskih vibracija.

Primjer:

Za slučaj $\Omega=\omega_0$ partikularno rješenje tražimo u obliku $x_p(t)=A \omega_0 t \sin{(\omega_0 t)}$. Uvrštavanjem u jednadžbu dobijemo da je $A=\frac{F}{2 k}$. Dakle, u tom slučaju opće je rješenje oblika

\begin{displaymath} x(t)= \alpha \cos(\omega_0 t-\phi)+\frac{F}{k} \omega_0 t \sin{(\omega_0 t)}. \end{displaymath}

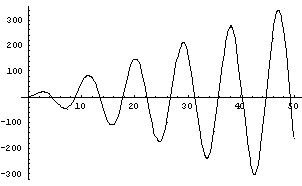
Ovo rješenje u vremenu eksplodira, tj. amplituda sve više raste.

Graf jednog ovakvog rješenja:

Image slika5

Primjer:

SUSTAVI S VIŠE STUPNJEVA SLOBODE

Sustavi s više stupnjeva slobode su oni sustavi koji zahtjevaju dvije, tri ili više koordinata da bi ih se u potpunosti moglo opisati. Jedan od najjednostavnijih primjera sustava s dva stupnja slobode može se vidjeti na jednoj od idućih animacija. Prikazane su dvije mase pričvršćene oprugama za zid, čije ponašanje opisuju dvije linearne koordinate $x_1$ i $x_2$.

Kao dobar primjer sustava s tri stupnja slobode mogli bismo uzeti sustav koji se sastoji od tri kuglice povezane nitima i predstavlja tek nešto kompliciraniju verziju matematičkog njihala (taj primjer također se može vidjeti na jednoj od idućih animacija). U tom slučaju položaje kuglica očito možemo odrediti koordinatama $x_i, y_i, i=1,2,3$. No, odmah se može uočiti da nisu potrebne obje od koordinata $x_i, y_i$, budući su one povezane relacijom $x_i^2+y_i^2=l^2$. Umjesto koordinata koje određuju položaj kuglica, mogli bismo koristiti i samo iznose kuteva $\theta_i$ jer su duljine niti u sustavu konstantne, te je pomoću kutova položaj kuglice u potpunosti određen. Bilo da koristimo kuteve ili pak neke od $x_i, y_i$ koordinata, uvijek će nam biti potrebno samo tri (a ne šest) da u potpunosti opišemo ponašanje sustava.

Koordinate koje koristimo za opisivanje sustava zovemo generalizirane koordinate i najčešće ih označavamo s $q_i$. Kao što smo upravo vidjeli, to mogu biti Kartezijeve i nekartezijeve koordinate.

Često se, da bi se jasnije mogle uočiti pojedine bitne karakteristike oscilacija sustava s više stupnjeva slobode, cjelokupno ponašanje sustava razlaže na njegove osnovne komponente. Te osnovne komponente predstavljaju one najbitnije elemente gibanja sustava i nazivaju se osnovni modovi ponašanja (gibanja). Ponašanje čitavog sustava tada se može prikazati kao superpozicija (linearna kombinacija) njegovih osnovnih modova. Kako je postupak nalaženja osnovnih modova ponešto kompliciraniji, ovdje se nećemo upuštati u njegovo matematičko opisivanje, ali na slijedećim animacijama vizualno će se moći uočiti o čemu je tu otprilike riječ.


Primjeri

Vibracije s jednim stupnjem slobode: Vibracije s više (ali konačno) stupnjeva slobode: Vibracije s beskonačno stupnjeva slobode:

Download

Cjelokupni tekst u PDF formatu: vibracije.pdf
Tacoma Bridge - MPEG film (kraća verzija): tacoma.mpeg

Linkovi

Tacoma Bridge - AVI film (duža verzija): http://www.cse.polyu.edu.hk/~ctbridge/goodies/
Tacoma Bridge - još neki filmovi: http://didaktik.physik.uni-wuerzburg.de/~pkrahmer/home/galileo.html

Vrh stranice | Teorija | Primjeri | Download | Linkovi | Verzija za printanje