
| Teorija klasifikacije |  |  |
|
Sadržaj: 1. UvodU ovom članku navodimo neke važnije danas poznate rezultate teorije modela, grane matematičke logike koja razmatra razna svojstva modela pojedinih teorija i na osnovu tih svojstava nastoji dobiti informacije o samoj teoriji. Preciznije, proučavat ćemo područje koje se tradicionalno naziva teorijom klasifikacije ili ponekad strukturalnom teorijom modela. Cijelo područje nastalo je iz glasovitog rada Michaela D. Morleya u kojemu se dokazuje teorem kategoričnosti, jedan od osnovnih teorema moderne teorije modela. U ovom članku dajemo ideju dokaza spomenutog teorema te raspravljamo o brojnim posljedicama do kojih se došlo proučavanjem pojmova uvedenih u Morleyevu radu. Od čitatelja se podrazumijeva neko osnovno znanje formalne logike, no za samo razumijevanje članka dovoljno je intuitivno znati što su to formule i modeli prvog reda. Za formalne definicije moguće je, primjerice, konzultirati uvodno poglavlje o logici prvog reda u knjizi [V1]. Ako će se čitatelj koristiti citiranom knjigom, treba napomenuti da je u ovom članku korišten ponešto modificirani pristup, i to uglavnom iz razloga što se takav pristup ustalio u udžbenicima teorije modela. Kao prvo, napomenimo da se jednakost u ovom članku tretira posebno i za svaku teoriju smatramo da posjeduje dvomjesni relacijski simbol "=" koji se interpretira upravo kao jednakost. Nadalje, kada govorimo o pojmu teorije, uzet ćemo malo općenitiji pristup od onog zastupljenog u [V1]. Za nas će, naime, teorija naprosto biti proizvoljan skup rečenica. Također, jasno je da će struktura biti vezana za jezike teorije, no kako bismo izbjegli tehničke komplikacije, to izostavljamo gdje je moguće. Ponekad će nam ipak biti neophodno navesti da je L jezik neke teorije T, pa ćemo pisati L-teorija, L-struktura i L-formula kako bismo to naglasili. Nadalje, sva razmatranja u ovom radu provode se za teorije čiji je jezik konačan ili prebrojivo beskonačan. Za dokaze i razjašnjenja ovdje spomenutih rezultata čitatelj može konzultirati navedenu literaturu, s naglaskom na [DM], [DV] i [V1]. Jedno važno pitanje, koje je veoma dugo zaokupljalo matematičare, jest koliko modela može imati neka teorija. Ako nam je cilj konstruirati teoriju prvog reda koja bi opisivala realne brojeve, svakako bismo željeli da su jedino realni brojevi model te teorije, odnosno da naša teorija ima, do na izomorfizam, samo jedan model. Općenito se za teorije koje imaju jedinstven model govori da su kategorične. Međutim, poznati Löwenheim-Skolemov teorem raspršuje sve snove o optimalnom rješenju, odnosno kategoričnosti. Naime, spomenuti teorem govori nam kako svaka konzistentna teorija prvog reda ima model proizvoljno velike kardinalnosti, ako ima barem jedan beskonačan model. Iz toga vidimo da ne postoji teorija prvog reda koja će aksiomatizirati realnu analizu tako da ta aksiomatizacija bude kategorična. Kada je već želja kategoričnosti propala, pokušao se napraviti kompromis i vidjeti možemo li postići kategoričnost u nekom fiksiranom kardinalu. U tu svrhu uveden je pojam κ-kategoričnosti.
Proučavajući svojstva κ-kategoričnih teorija otkriveni su brojni zanimljivi rezultati o broju modela promatrane teorije u nekoj zadanoj kardinalnosti. Cijela priča počinje 1965. godine poznatim člankom Michaela Morleya pod naslovom "Categoricity in power". U tome članku dokazan je poznati Morleyev teorem koji se smatra prvim ozbiljnijim rezultatom u teoriji modela i koji je otvorio novo područje proučavanja - teoriju klasifikacije.
Za neku teoriju reći ćemo da je potpuna ako za svaku rečenicu te
teorije vrijedi da je ili ta rečenica, ili pak njezina negacija teorem te teorije.
Pritom pod pojmom teorem podrazumijevamo svaku posljedicu teorije.
Zamislimo sada da je zadana potpuna teorija T. Ako je κ
kardinalni broj, s I(T, κ) označavamo broj
neizomorfnih modela teorije T kardinalnosti κ.
Funkcija κ
Kao što vidimo, Morleyev teorem daje jedno iznimno zanimljivo svojstvo funkcije spektra. Naime, on nam govori da ako je I(T, κ) = 1 za jedan neprebrojiv kardinal κ, tada je I(T, λ) = 1 za sve neprebrojive kardinale λ. Već spomenuti članak uveo je mnoštvo pojmova koji su postali dio standardnog rječnika teorije modela i naveliko su se koristili u daljnjim istraživanjima svojstava spektra. U ovom članku dajemo pregled nekih osnovnih pojmova i rezultata vezanih uz teoriju klasifikacije. Cijeli članak bit će koncipiran na dokazu Morleyeva teorema uz digresije o daljnjim proučavanjima svojstava spektra. Možemo već unaprijed najaviti kako je problem spektra za potpune teorije u potpunosti razriješen za neprebrojive kardinale. Također ćemo pokazati koji se problemi i zanimljivosti javljaju pri proučavanju broja prebrojivih modela koji su detaljno proučavali Vaught, Morley i Shelah. 2. Osnovni pojmoviU ovom paragrafu uvodimo neke osnovne pojmove koji se koriste prilikom proučavanja spektra i dokaza Morleyeva teorema. TipoviSljedeći pojam, pojam tipa, osnovni je pojam koji se javlja u svakom proučavanju u teoriji modela. Ideja je vrlo jednostavna. Naime, ono što nas zanima o nekom modelu je ono što je u njemu istinito.
Napomenimo prvo da ćemo sa
Σ(x1,…,xn)
označavati skup formula u
kojima se jedino varijable iz skupa
{x1,…,xn} mogu javiti kao
slobodne.
S
Obično ćemo se koristiti standardnom pokratom x za n-torku varijabli (x1,…,xn), za neki 1 ≤ n < א0. Nadalje, zanimat će nas koji su to elementi modela kojima se varijable moraju valuirati da bi formule bile istinite. Također, uglavnom ćemo proučavati potpune tipove, kao analogone potpunih teorija.
Lako je provjeriti da je svaki
tp TopologijaNeka je T neka teorija u jeziku L. Sa Sn(T) označavamo skup svih potpunih n-tipova teorije T. Za formulu Φ(x) sa slobodnim varijablama u skupu {x1,…,xn} s XΦ označavamo skup XΦ = {p ∈ Sn(T) : Φ ∈ p}. Na skupu Sn(T) uzimamo topologiju definiranu bazom koju čine svi skupovi XΦ, pri čemu je Φ proizvoljna formula u jeziku teorije T, čije se slobodne varijable nalaze u {x1,…,xn}. Trivijalno je za provjeriti kako je to doista baza neke topologije na skupu Sn(T). Nadalje, budući da za potpun tip teorije T i proizvoljnu formulu Φ vrijedi da je ili Φ ∈ p ili ¬Φ ∈ p, jasno je da vrijedi XΦ = Sn(T) \ X¬Φ. Dakle, svaki bazni otvoreni skup topološkog prostora Sn(T) je ujedno i otvoren i zatvoren. Također je moguće provjeriti da je Sn(T) kompaktan Hausdorffov prostor. Napomenimo da kompaktnost prostora slijedi iz teorema kompaktnosti za logiku prvog reda. Premda se upletanje topologije u logiku čini neuobičajenim, ono olakšava velik broj dokaza. Također je zanimljivo vidjeti kako se dvije naočigled nepovezane grane matematike međusobno isprepleću. Saturirani modeli
Razjasnimo još jednu oznaku. Ako
je Iznimno važna klasa modela koja se pojavljuje u dokazima mnogih teorema su saturirani modeli, odnosno saturirane strukture.
Uočimo da je svaki potpuni tip neke teorije realiziran u nekom njezinom modelu. Saturiranost modela jamči nam da je svaki potpuni tip realiziran baš u tom modelu. Navedimo sada nekoliko primjera saturiranih, odnosno nesaturiranih modela.
Jedinstvenost modela
Za dvije strukture
Napomenimo da se za dokaz prethodnog teorema koristi tipična "back-and-forth" konstrukcija kakva se često pojavljuje u teoriji modela. Inače, jedna od poznatijih "back-and-forth" konstrukcija je dokaz teorema o uređajnoj karakteristici skupa racionalnih brojeva, čiji se dokaz može naći u [V2]. Čitanjem samo jednog smjera dokaza prethodnog teorema dobivamo sljedeće:
Pod pojmom elementarnog ulaganja mislimo na izomorfizam
između Premda je jedinstvenost saturiranih modela poželjno svojstvo, još se nismo bavili pitanjima egzistencije. Sljedeći teorem daje nam djelomičan odgovor na ovo pitanje, a egzistencija saturiranih modela tvorit će znatan dio dokaza Morleyeva teorema, kao što će se kasnije pokazati.
Dakle, ako imamo neki model i dovoljno velik kardinalni broj τ, možemo naći elementarno proširenje našeg modela koje će biti τ+-saturirano. Naglasimo da posebno uvijek možemo naći ω-saturirano proširenje. Monster model
Demonstrirajmo sada zašto su nam prethodna razmatranja o jedinstvenosti
i egzistenciji saturiranih modela korisna.
Pretpostavimo da je T potpuna teorija i da želimo proučavati njezine modele
kardinalnosti manje ili jednake κ, pri čemu je κ beskonačni kardinalni broj.
Neka je 3. Prebrojivi spektarKao što smo već napomenuli, cilj ovog članka je proučavanje funkcije spektra potpunih teorija u prebrojivom jeziku. U ovom paragrafu prikazat ćemo što je poznato o broju prebrojivih modela neke teorije, odnosno o prebrojivu spektru. Kroz godine proučavanja došlo se do mnogih primjera. Prvo što se pokušalo pronaći su teorije s konačnim brojem prebrojivih modela. Poznati Cantorov teorem o uređajnoj karakteristici skupa racionalnih brojeva govori nam kako teorija gustih potpunih uređaja bez krajnjih točaka, DLO, ima točno jedan prebrojiv model. Dokaz spomenutog teorema moguće je naći u [V2]. Također, uz ponešto tehničkih komplikacija, pronađeni su i primjeri teorija s tri ili više prebrojivih modela. Naime, vrijedi sljedeće:
Dokaz prethodno navedene leme moguće je naći u [DM] ili [AP]. Budući da je teorija modela od svojih početaka bila blisko povezana s proučavanjem algebarskih struktura, dobiveni su i rezultati o teoriji algebarski zatvorenih polja ACFp neke fiksne karakteristike p te o teoriji realnih zatvorenih polja RCF. Za detalje o spomenutim teorijama konzultirati [DM]. Sumirajmo neke poznate činjenice o mogućem broju prebrojivih modela.
Budući da postoji najviše 2א0 neizomorfnih prebrojivih modela potpune teorije T (toliko, naime, ima relacija na prebrojivu skupu), postavljaju se dva prirodna pitanja:
Iznenadujuće je što je na prvo pitanje Vaught odgovorio negativno. Točnije, vrijedi sljedeći teorem čiji se detaljan dokaz može pronaći u [DM].
U slučaju da je hipoteza kontinuuma istinita, drugo pitanje ima trivijalno negativan odgovor. Vaught je postavio hipotezu koja govori da je odgovor negativan čak i u slučaju da je hipoteza kontinuuma neistinita. Shelah je dokazao da Vaughtova hipoteza vrijedi za klasu tzv. ω-stabilnih teorija (vidjeti definiciju 4.1). Postoji još nekoliko sličnih rezultata koji govore o tome da Vaughtova hipoteza vrijedi za neku specifičnu klasu teorija. Međutim, najjači generalni rezultat je onaj M. Morleya (ne miješati s teoremom kategoričnosti!) koji glasi:
Navedeni teorem zapravo nam govori kako je mogući broj prebrojivih modela manji ili jednak א0, ili je א1, ili je pak 2א0. Vaughtova hipoteza smatra se jednim od najvažnijih otvorenih problema teorije modela i oko nje postoje neke kontroverze. Robin Knight je 2002. godine objavio protuprimjer za Vaughtovu hipotezu, no još uvijek nije utvrđen službeni status tog rada. Zainteresirani čitatelj može pronaći rad na Knightovoj web stranici [RK]. 4. Morleyev teorem i broj neprebrojivih modelaStabilnost i nerazlučivostMorleyev teorem, premda jednostavan i lako razumljiv, ima poprilično težak dokaz. U svojem članku Morley je uveo mnogo novih pojmova koji su postali standardni u teoriji modela i čije je proučavanje dovelo do mnogo važnih rezultata u teoriji klasifikacije. Jedan od ključnih pojmova je stabilnost.
Na analnogan se način definira i pojam λ-stabilne teorije, gdje je λ proizvoljan kardinalni broj. Stabilnost nam zapravo govori da prostor tipova ne postaje prevelik ako teoriju proširimo novim konstantama. Napomenimo da se ovdje navodi naziv ω-stabilnost iz povijesnih razloga, premda je riječ o kardinalnim brojevima. Naime, ω je tradicionalna oznaka za ordinalni broj koji je ujedno i kardinalni broj koji se označava s א0. Međutim, u literaturi se uvriježio pojam ω-stabilnosti. Sljedeći fundamentalni pojam koji se javlja je pojam nerazlučivih nizova.
Pritom pod
tp Za određivanje nekih svojstava modela važna nam je egzistencija nerazlučivih nizova. Sljedeći rezultat daje nam pomalo iznenadujuću činjenicu o nerazlučivim nizovima. Naime, za teoriju s beskonačnim modelima možemo pronaći proizvoljno duge nerazlučive nizove u nekom modelu od T.
Napomenimo da se za dokaz egzistencije nerazlučivih nizova potrebno koristiti verzijom Ramseyeva teorema o svojstvima beskonačnih skupova, koji je jedan od osnovnih rezultata kombinatorike beskonačnih skupova. Sama grana kombinatorike beskonačnih skupova korištena je u dubljim proučavanjima unutar teorije klasifikacije i do mnogih važnih rezultata došlo se u želji da se pokaže kakva je struktura modela pojedinih teorija. Veliku ulogu u tome imao je Saharon Shelah, autor monumentalnog djela pod nazivom "Classification theory", koje se još i danas smatra jednim od vrhunaca teorije modela. Osvrnimo se sada na još jednu zanimljivu primjenu nerazlučivih nizova. Kao što znamo, Gödelov prvi teorem nepotpunosti govori nam o egzistenciji aritmetičke rečenice Φ koja je istinita, no nedokaziva u Peanovoj aritmetici. Premda gnoseološki zanimljiva, Gödelova rečenica nije pretjerano korisna kao matematički teorem. Paris i Harrington kasnih su sedamdesetih pokazali da je jedna varijanta Ramseyeva teorema istinita, ali da je nedokaziva u Peanovoj aritmetici (preciznije, neovisna o aritmetici, odnosno neodlučiva). Zanimljivo je da ta varijanta čak ne spada u kombinatoriku beskonačnih skupova već govori o konačnim skupovima. Dokaz se koristi nerazlučivim nizovima, ali i klasičnim kodiranjem koje se javlja još kod Gödela. Posljedice stabilnostiKao što smo napomenuli, ω-stabilne teorije igraju iznimno važnu ulogu u dokazu Morleyeva teorema i u samoj teoriji modela. Zapravo, velik broj istraživanja, posebice onih algebarske naravi, radi se pod pretpostavkom stabilnosti. Sljedeći teorem govori nam da se za dokaz Morleyeva teorema možemo koristiti stabilnim teorijama.
Još jedan važan pojam je pojam Morleyeva ranga, no budući da je sama definicija suviše tehnička, ovdje je izostavljamo. Napomenimo samo da se Morleyev rang formule Φ(x, a) s parametrima a označava RM(Φ(x, a)), da je to ordinalni broj (ili ∞) i da nam govori nešto o definabilnim skupovima i njihovom particioniranju s pomoću formula zadane teorije. Za detalje konzultirati [DV], gdje se mogu pronaći detaljna definicija i karakterizacija te način na koji se Morleyev rang može promatrati neovisno o modelu iz kojeg dolaze parametri formule Φ. Napomenimo još da se Morleyev rang može promatrati i kao vrlo apstraktan pojam dimenzije koji se u nekim specifičnim slučajevima poklapa sa prirodnim pojmom dimenzije. Sljedeći rezultat daje nam uvid u vezu između Morleyeva ranga i stabilnih teorija. On nam zapravo kaže da je ω-stabilnost ekvivalentna tome da je Morleyev rang definiran za sve formule proučavane teorije.
Primijetimo da smo u prethodnom teoremu naveli kako ω-stabilnost povlači stabilnost u svim beskonačnim kardinalima. Općenito se možemo pitati koje su mogućnosti za stabilnost neke potpune teorije u beskonačnim kardinalima. Shelah je u potpunosti odgovorio na to pitanje u sljedećem teoremu.
Već smo napomenuli da su nam saturirani modeli iznimno važni za dokaz Morleyeva teorema. Sljedeći rezultat govori nam o jednoj posljedici kategoričnosti, no proučavajući dokaz teorema, može se vidjeti da je to u biti posljedica stabilnosti promatrane teorije.
Sljedeća propozicija, koja će biti ključna za dokaz, govori nam da ω-stabilne teorije imaju poželjno svojstvo nasljeđivanja saturiranosti.
Morleyev teoremKoristeći se prethodnim rezultatima sada možemo dokazati Morleyev teorem kategoričnosti.
Naime, pokazali smo da je svaka κ-kategorična teorija T ujedno i ω-stabilna. Nadalje, iz teorema 4.7 znamo da postoji saturiran model od T kardinalnosti κ. Kako je T κ-kategorična, svi modeli od T kardinalnosti κ su saturirani, pa je prema prethodnoj propoziciji za svako λ > א0 svaki model od T kardinalnosti λ saturiran. Kako su svaka dva modela potpune teorije elementarno ekvivalentna, prema jedinstvenosti saturiranih modela (teorem 2.5), teorija T je λ-kategorična. Time je dovršen dokaz teorema. Ugrubo govoreći, dokaz se može razdijeliti u tri dijela. U prvom se dijelu iz svojstva kategoričnosti izvodi ω-stabilnost, u drugom se s pomoću stabilnosti i kategoričnosti dokazuje egzistencija saturiranih modela, a u trećem se dokazuje sam teorem. Alternativno, do Morleyeva teorema kategoričnosti može se doći koristeći se Baldwin-Lachlanovim teoremom:
Budući da ω-stabilnost i Vaughtovi parovi ne ovise o kardinalu κ, jednostavno dobivamo Morleyev teorem. Za detalje o tome što je Vaughtov par i o dokazu samog teorema vidjeti [DM]. Neprebrojivi spektarSumirajmo što do sada znamo o neprebrojivom spektru.
Morley je postavio hipotezu da je funkcija
κ Proširujući Shelahov rad, Bradd Hart, Ehud Hrushovski i Michael C. Laskowski u potpunosti su razriješili problem spektra u neprebrojivim kardinalima. Njihov rad pokazuje da je moguće trinaest različitih slučajeva za broj neprebrojivih modela potpune prebrojive teorije T. Također, za svaki od tih slučajeva pronađen je primjer teorije s točno toliko modela. Za detalje konzultirati [HL]. Literatura
1. Uvod |

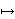 I(T, κ) naziva se spektrom
teorije T. Proučavanje spektra vrlo je važan problem u teoriji
modela koji započinje sljedećim teoremom.
I(T, κ) naziva se spektrom
teorije T. Proučavanje spektra vrlo je važan problem u teoriji
modela koji započinje sljedećim teoremom.
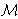
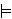 Σ[a1,…,an]
ćemo označavati da je svaka formula iz Σ istinita za
valuaciju u kojoj je varijabla xi valuirana
elementom ai,
za i = 1,…,n.
Σ[a1,…,an]
ćemo označavati da je svaka formula iz Σ istinita za
valuaciju u kojoj je varijabla xi valuirana
elementom ai,
za i = 1,…,n.
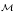 (
(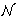 reći ćemo
da su elementarno ekvivalentne ako je
Th(
reći ćemo
da su elementarno ekvivalentne ako je
Th(