
 |
Hrvatski matematički elektronski časopis math.e | |
| Broj 12 | ||
| http://e.math.hr/ |
Sadržaj:
1. Uvodni zadaci
2. Kombinatorički dizajni
3. Preslikavanja dizajna
4. Najmanji 2-dizajn i poopćenje
Literatura
Prva postava hrvatske muške rukometne reprezentacije na 20. svjetskom rukometnom prvenstvu održanom u Njemačkoj 2007. godine bila je:
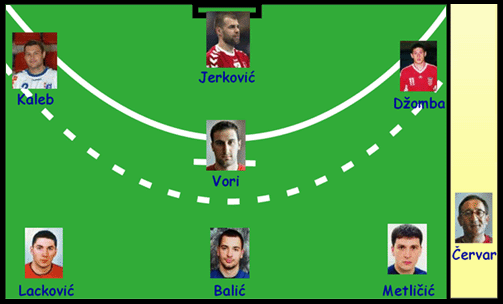
Prva postava nije bila ista na svakoj utakmici, ali najčešće je utakmica započinjala u gore navedenom sastavu (za detalje vidi [IHF]).
Zadatak 1. Televizijska kuća koja prati Svjetsko muško rukometno prvenstvo odlučila je kao najavu uoči svake utakmice napraviti razgovor s trojicom igrača prve sedmorke. Kako neki igrači ne bi bili favorizirani, odlučeno je da se svaka dva igrača susretnu točno jednom. Televizijska kuća predvidjela je da će se Hrvatska plasirati u drugo kolo, odnosno da će odigrati barem 7 utakmica (3 utakmice u skupini prvoga kruga natjecanja i 4 utakmice u skupini drugoga kruga natjecanja). Napravite raspored televizijskih razgovora s igračima!
Rješenje. Jedan od mogućih rasporeda dan je u tablici.
| Utakmica | Igrači |
|---|---|
| 1. utakmica | Džomba, Lacković, Jerković |
| 2. utakmica | Jerković, Metličić, Balić |
| 3. utakmica | Balić, Kaleb, Džomba |
| 4. utakmica | Džomba, Vori, Metličić |
| 5. utakmica | Lacković, Vori, Balić |
| 6. utakmica | Jerković, Vori, Kaleb |
| 7. utakmica | Lacković, Metličić, Kaleb |
Zadatak 2. Napravite raspored najava kao u prvom zadatku, ali tako da utakmice mogu najavljivati igrači prve sedmorke i trener Lino Červar.
Pokušaj rješenja. Prvu utakmicu najavljivat će Džomba, Lacković i Jerković. Krenimo na drugu utakmicu. Neka je opet najavljivač Džomba, ali mu više ne smiju društvo praviti Lacković i Jerković (zbog uvjeta zadatka da se svaka dva igrača moraju susresti točno jednom). Pa neka najavu druge utakmice odrade Džomba, Balić i Metličić. Nadalje, treću utakmicu može opet najavljivati Džomba, ali ne u istom društvu kao pri najavi prve ili druge utakmice. Uzmimo Džombu, Kaleba i Červara za najavu treće utakmice.
Svaka dva igrača moraju se susresti točno jednom pa Džomba mora odraditi još jednu najavu pri kojoj će mu društvo praviti Vori, ali par Džomba-Vori ne možemo ni na koji način nadopuniti trećim igračem jer bi taj igrač i Džomba odradili zajedno dvije najave, što je u suprotnosti s uvjetima zadatka.
Pokušamo li složiti ovaj raspored na neki drugi način, počevši s nekim drugim igračima, doći ćemo do istog problema. Što možemo zaključiti? Za sada zaključujemo da zadatak ne znamo riješiti.
Objašnjenje razloga zbog kojih prvi zadatak znamo i možemo riješiti, a u drugom zadatku dolazimo do problema potražit ćemo u matematici. Posebno, u teoriji dizajna.
Začetkom teorije dizajna smatra se Kirkmanov problem učenica iz 1850. godine (vidi [WE] i [WI]):
Petnaest učenica svakoga dana hoda do škole u pet grupa po tri učenice. Može li se napraviti tjedni raspored grupa tako da svaki par učenica bude u istoj grupi samo jednom?
Jedan od mogućih tjednih rasporeda dan je u sljedećoj tablici.
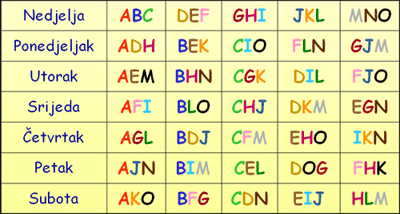
Intenzivan razvoj teorije dizajna započeo je proučavanjem statističkih eksperimentalnih dizajna u planiranju eksperimenata u biologiji tridesetih godina 20. stoljeća (vidi [AC]).
Dizajn s parametrima 2-(v,k,λ)
je par (P,B) koji zadovoljava uvjete:
|
Primjer. Dizajn s parametrima 2-(7,3,1) prikazan je na sljedećoj animiranoj slici.
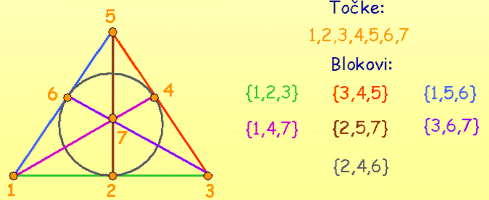
Postavlja se pitanje postoji li dizajn za svaki izbor parametara v, k, i λ. Odgovor je: ne postoji! Za početak, parametri 2-dizajna moraju zadovoljavati nuždan uvjet koji ćemo izvesti iz definicije 2-dizajna.
Neka je P jedna točka dizajna. Prebrojimo uređene parove (Q, blok koji sadrži točke P i Q) u 2-(v,k,λ) dizajnu.
Točku Q različitu od točke P možemo odabrati na v−1 načina. Blok koji sadrži točke P i Q možemo odabrati na λ načina (zato što su svake dvije točke sadržane u točno λ blokova). Odnosno, prebrojili smo (v−1)·λ parova.
S druge strane, neka je n broj blokova koji sadrže točku P. Svaki od tih blokova sadrži još k−1 točaka (zato što svaki blok sadrži točno k točaka). Odnosno, prebrojili smo n·(k−1) parova.
Na dva smo načina prebrojili iste uređene parove pa vrijedi λ·(v−1) = n·(k−1). Broj blokova koji sadrže točku P je n = λ·(v−1)/(k−1). To mora biti prirodan broj, pa zaključujemo: k−1 dijeli λ·(v−1). Taj uvjet je nuždan uvjet postojanja 2-(v,k,λ) dizajna.
Vratimo se ponovno na zadatke s početka. "Prevedimo" prvi zadatak na jezik dizajna: rukometaše možemo predstaviti točkama, a trojke igrača koje najavljuju jednu utakmicu blokovima. Odnosno, broj točaka je 7, blokovi su tročlani podskupovi skupa točaka i svake dvije točke nalaze se u točno jednom zajedničkom bloku. Raspored najava iz prvog zadatka moguće je složiti zato što postoji 2-(7,3,1) dizajn. Tablica kojom je opisano rješenje zadatka dobivena je identifikacijom igrača s točkama dizajna:
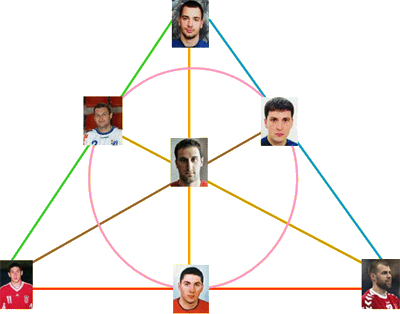
"Prevedimo" drugi zadatak na jezik dizajna: v = 8, k = 3, λ = 1. Kako 2 ne dijeli 7, parametri dizajna 2-(8,3,1) ne zadovoljavaju nuždan uvjet pa zaključujemo da 2-(8,3,1) dizajn ne postoji. Odnosno, ne postoji raspored najava koji zadovoljava uvjete drugog zadatka.
Zadatak 3. Neka je zadan jedan raspored najava utakmica (naprimjer, kao u rješenju Zadatka 1). Na koliko načina možemo zamijeniti igrače tako da raspored igrača unutar trojki koje najavljuju utakmice ostane isti?
Rješenje.
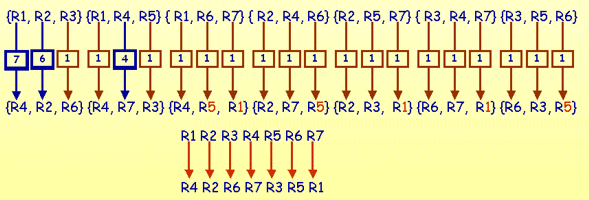
Neka je složen jedan raspored najava utakmica (naprimjer, prvu utakmicu najavljuju igrači R1, R2, R3). Rukometaša R1 možemo ne zamijeniti ili ga možemo zamijeniti bilo kojim od preostalih 6 rukometaša (naprimjer, rukometašem R4). Prebrojili smo 7 mogućnosti za zamjenu rukometaša R1. Nakon toga, rukometaša R2 (koji je također najavljivao prvu utakmicu) možemo zamijeniti svakim rukometašem osim onim koji mijenja rukometaša R1, odnosno na 6 načina (naprimjer, zamijenimo ga rukometašem R2, odnosno ne mijenjamo ga). Zamjene (u našem primjeru rukometaši R4 i R2) početnih najavljivača prve utakmice u prvobitnom rasporedu najavljivali su jednu od utakmica, zbog uvjeta prvog zadatka koji kaže da se svaka dva igrača moraju susresti točno jednom (u primjeru iz animacije najavljivali su četvrtu utakmicu). Osim njih dvojice, četvrtu utakmicu najavljivao je još jedan rukometaš (u našem primjeru rukometaš R6). Iz uvjeta zadatka koji rješavamo (da raspored igrača unutar svake trojke mora ostat isti) slijedi da rukometaš R6 mora mijenjati rukometaša R3. Zamijenili smo rukometaše koji su najavljivali prvu utakmicu. Napravit ćemo isto s rukometašima koji najavljuju drugu utakmicu. Sljedećeg igrača kojega još nismo zamijenili (u našem primjeru igrača R4) možemo zamijeniti na 4 načina (igračima koji nisu uključeni u zamjenu igrača R1, R2, R3). Zamjena trećeg igrača koji je najavljivao drugu utakmicu je opet jednoznačno određena (na isti način kao i prije). Kao što vidimo na animaciji, i preostale zamjene su jednoznačno određene.
Zaključujemo da je zamjene igrača uz uvjete zadatka moguće napraviti na 7·6·4 = 168 načina.
Zamjene točaka u dizajnu uz uvjete prethodnog zadatka zovemo automorfizmima dizajna. Odnosno, automorfizam 2-(v,k,λ) dizajna je bijekcija f koja skup P preslikava u skup P i pritom skup B preslikava u skup B (pretpostavljamo da f preslikava k-člani skup točaka u skup slika tih točaka).
Slijedi da smo treći zadatak mogli zadati na sljedeći način: koliko ima automorfizama 2-(7,3,1) dizajna?
Neka je A1A2A3A4A1 pravilan peterokut i neka je A6 središte kružnice opisane tom peterokutu.
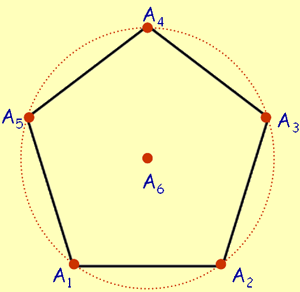
Zadatak 4. Koliko ima trokuta kojima su vrhovi neke tri od šest zadanih točaka i čija se jedna stranica poklapa sa stranicom peterokuta? Koji dizajn je opisan ovim modelom? Što su točke, a što blokovi tog dizajna?
Rješenje.
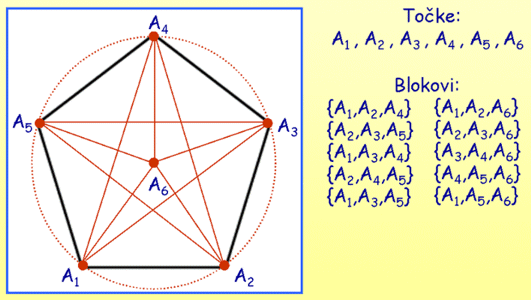
Zaključujemo, navedeni primjer opisuje 2-(6,3,2) dizajn. Taj dizajn ujedno je i najmanji netrivijalni 2-dizajn.
Zamijenimo li u definiciji 2-(v,k,λ) dizajna prirodan broj 2 bilo kojim prirodnim brojem t ≥ 2, dobit ćemo definiciju t-dizajna:
Dizajn s parametrima t-(v,k,λ)
je par (P,B) koji zadovoljava uvjete:
|
Poopćenjem dokaza nužnog uvjeta za postojanje 2-dizajna dobivamo nuždan uvjet postojanja t-(v,k,λ) dizajna: (k−1)(k−2)…(k−t+1) dijeli λ(v−1)(v−2)…(v−t+1).
Zadatak 5. Trener Lino Červar ima na raspolaganju 14
rukometaša (12 igrača i 2 golmana) i želi napraviti raspored
šestorki (postava bez golmana) koje će se uigravati na treningu
tako da se:
(a) svaka petorica igrača uigravaju točno jednom,
(b) svaka četvorka igrača uigrava točno tri puta.
Može li trener Červar složiti takav raspored?
Rješenje.
(a) Može se složiti raspored za zadane uvjete jer postoji 5-(12,6,1) dizajn (vidi [CV]). Treneru Červaru bit će potrebna 132 treninga da iskoristi sve mogućnosti.
(b) Raspored uigravanja postoji ako postoji 4-(12,6,3) dizajn. Taj dizajn ne postoji jer njegovi parametri ne zadovoljavaju nuždan uvjet: (k−1)(k−2)…(k−t+1) = 5·4·3 = 60 ne dijeli λ(v−1)(v−2)…(v−t+1) = 3·11·10·9 = 2970.
| [AC] | I. Anderson, C.J. Colbourn, J.H. Dinitz i T.S. Griggs, Design theory: antiquity to 1950, Handbook of combinatorial designs, drugo izdanje, urednici: C.J. Colbourn i J.H. Dinitz, Chapman & Hall / CRC, Boca Raton, 2007, 11-20. |
| [CV] | P.J. Cameron i J.H. Van Lint, Designs, graphs, codes, and their links, Cambridge University Press, 1991. |
| [IHF] | International Handball Federation (studeni 2007.). http://www.ihf.info |
| [WE] | E.W. Weisstein, Kirkman's schoolgirl problem (studeni 2007.). http://mathworld.wolfram.com/KirkmansSchoolgirlProblem.html |
| [WI] | Wikipedia: The Free Encyclopedia, Kirkman's schoolgirl problem (studeni 2007.). http://en.wikipedia.org/wiki/Kirkman's_schoolgirl_problem |
1. Uvodni zadaci
2. Kombinatorički dizajni
3. Preslikavanja dizajna
4. Najmanji 2-dizajn i poopćenje
Literatura