Hrvatski matematički elektronski časopis math.e

http://web.math.hr/mathe/

Iz povijesti matematike

Ivica Gusić: Zašto su uvedeni kompleksni brojevi


Uobičajeno je mišljenje da su kompleksni brojevi uvedeni u matematiku da bi svaka kvadratna jednadžba imala rješenje (na primjer, jednadžba x2 + 1 = 0 nema realnih rješenja, a nakon uvođenja kompleksnih brojeva ima dva rješenja: i i -i). To se kasnije podupire još jačim argumentom da svaka algebarska jednadžba stupnja n ima točno n rješenja (uključujući kratnost). Na primjer, jednadžba

x4 - 2x3 + 2x2 - 2x + 1 = 0

ima točno četiri rješenja: dvostruko rješenje 1 i jednostruka rješenja i, -i. To se obrazlaže rastavom na faktore:

x4 - 2x3 + 2x2 - 2x + 1 = (x - 1)2 (x2 + 1)

za svaki realni (odnosno kompleksni) broj x, odnosno rastavom

x4 - 2x3 + 2x2 - 2x + 1 = (x - 1)2 (x - i) (x + i).

Ponekad se uvođenje kompleksnih brojeva obrazlaže Bézoutovim poučkom:

Dvije algebarske krivulje reda m, odnosno n, sijeku se u točno mn točaka (računajući kratnosti i točke u beskonačnosti).

Takav poučak ne bi vrijedio bez kompleksnih brojeva. Na primjer, pravac ne bi sjekao koniku u točno dvjema točkama i općenito krivulju reda n u n točaka. Na primjer, pravac s jednadžbom y = x + 2 ne siječe kružnicu s jednadžbom x2 + y2 = 1 (ako se razmatraju samo realne točke), međutim, siječe je u točkama

(-1 - √2 / 2 i, 1 - √2 / 2 i)   i   (-1 + √2 / 2 i, 1 + √2 / 2 i).

Svi ovi (i neki drugi) razlozi matematičarima su dobar povod za uvođenje korijena od negativnih brojeva, a time i kompleksnih brojeva. Međutim, ni u jednome od njih kompleksni brojevi nisu bili nužni.

U vrijeme uvođenja kompleksnih brojeva u matematiku (u 16. stoljeću) kvadratna je jednadžba bila poznata više od 3000 godina. Stari su je matematičari već rješavali i znali su da može imati dva, jedno ili nijedno rješenje i to im je bilo dovoljno. Također se naslućivalo da algebarska jednadžba stupnja n ima najviše n rješenja (tu se misli samo na jednadžbu s realnim koeficijentima i samo na realna rješenja jer za druge nisu ni znali).

Razlogom za uvođenje kompleksnih brojeva mogao je biti samo matematički problem u kojemu se kompleksni brojevi nisu mogli zaobići, a takav se problem pojavio pri rješavanju kubne jednadžbe. O čemu je riječ ukratko ćemo govoriti u nastavku. Kako je poznato, svaka je kubna jednadžba ekvivalentna jednadžbi oblika

x3 + ax2 + bx + c = 0

gdje su a,b,c realni brojevi (danas to mogu biti i kompleksni brojevi ili elementi nekog polja). S takvim su jednadžbama matematičari imali poteškoća više od 3000 godina dok ih u prvom dijelu 16. stoljeća nisu uspjeli "ukrotiti". Neke je od tih jednadžbi lako riješiti; primjerice jednadžba x3 - x = 0 ima rješenja 0, 1, -1. Slično je za svaku kubnu jednadžbu s racionalnim koeficijentima (tj. jednadžbu za koju je a, b, c 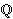iz Q), koja ima bar jedno racionalno rješenje. Naime, kod takvih jednadžbi u pravilu je lako naći racionalno rješenje r = p / q; p,q 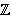iz Z. Nakon što jednadžbu pomnožimo sa zajedničkim višekratnikom svih koeficijenata, p mora dijeliti slobodni, a q vodeći koeficijent jednadžbe. Kako ima konačno takvih mogućnosti, načelno možemo doći i do one povoljne. Kad znademo racionalno rješenje r, onda dijeljenjem možemo doći do rastava:

x3 + ax2 + bx + c = (x - r) (x2 + a'x + b')

pa se preostala rješenja početne kubne jednadžbe dobiju rješavanjem kvadratne jednadžbe x2 + a'x + b' = 0. Takve se kubne jednadžbe često pojavljuju u srednjoškolskim zadatcima, a i na sveučilištu. Međutim, što je s jednadžbom

x3 - 6x + 2 = 0 ?

Pokušajte je riješiti! O toj ćemo jednadžbi više reći poslije, a sada se poslužimo sličnim argumentima kao i za kubne jednadžbe s racionalnim koeficijentima i s barem jednim racionalnim rješenjem kako bismo zaključili da svaka kubna jednadžba s realnim koeficijentima ima barem jedno realno rješenje (ukupno 3 kompleksna rješenja, uključujući kratnosti). Izraz x3 + ax2 + bx + c za dovoljno je velike pozitivne x-eve pozitivan, a za dovoljno male negativne x-eve negativan, pa je za neki x jednak nuli. Zaključujemo da jednadžba x3 + ax2 + bx + c = 0 ima bar jedno realno rješenje r. Sada je

x3 + ax2 + bx + c = (x - r) (x2 + a'x + b')

pa mogu nastupiti sljedeće mogućnosti:

(i)    jednadžba ima 3 realna različita rješenja,

(ii)   jednadžba ima 1 realno jednostruko i 1 realno dvostruko rješenje,

(iii)   jednadžba ima 1 realno trostruko rješenje,

(iv)   jednadžba ima jedno realno i dva konjugirano kompleksna rješenja.

U doba otkrivanja formula za rješenje kubne jednadžbe nije bilo kompleksnih brojeva pa su (iv) ondašnji matematičari shvatili kao

(iv)'   jednadžba ima 1 rješenje.



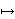Formula za rješenje kubne jednadžbe


Dovoljno je razmatrati jednadžbu x3 + px + q = 0, gdje su p, q realni brojevi (to se dobije zamjenom x - a/3 |--> x). Ako napišemo x = u + v, uz uvjet uv = -p/3, dolazimo do sustava

u3 + v3 = -q,
u3 * v3 = -p3/27,

odakle je

x = 3√ -q/2 + √(q2/4 + p3/27) + 3√ -q/2 - √(q2/4 + p3/27)

(to je prikaz rješenja x u obliku u + v). Ta se formula zove Cardanova formula (prema talijanskom matematičaru koji je tu formulu objavio 1545. g. u djelu Artis Magnae).

Pogledajmo kako su se matematičari u početku koristili tom formulom.


Primjer 1:     x3 + 3x + 2 = 0,   p = 3,   q = 2.

x = 3√ -1 + √2 + 3√ -1 - √2 = 3√ -1 + √2 - 3√ 1 + √2.

Tada su matematičari znali samo za realne brojeve i tu nije bilo problema:

u = 3√ -1 + √2, v = - 3√ 1 + √2, uv = 3√ -1 √2 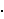* (- 3√ -1 + √2 ) = - 3√-1 = -1

(naime, 3√ je za njih jednoznačna neparna funkcija definirana za sve realne brojeve, a √ je definiran za nenegativne realne brojeve). Tako je dobiveno jedinstveno rješenje početne jednadžbe. To se može i provjeriti. Ta jednadžba ima i dva kompleksno-konjugirana rješenja, međutim, matematičari 16. st. o tome na početku nisu vodili računa, niti im je, u ovom slučaju, to bilo potrebno.


Primjer 2:     x3 - 3x = 0.


Za tu jednadžbu ne treba formula. Odmah se vidi da su rješenja x1 = 0, x2,3 = 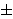+- √3. Pokušajmo ipak primijeniti formulu. Tu je p = -3, q = 0, pa je

x = 3√√-1 + 3√-√-1.         (*)

Vidimo da nas Cardanova formula, u ovom jednostavnom slučaju, dovodi do teških problema - drugih korijena iz negativnih brojeva. To je navelo matematičare 16. st. da se pozabave i takvim matematičkim objektima. Ako su ovakav slučaj mogli i zanemariti (jer već znaju rješenja: 0, √3, -√3), neke su im jednadžbe stvarale još veće poteškoće.


Primjer 3:     x3 - 6x + 2 = 0.


Lako se vidi da ta jednadžba nema racionalnih rješenja. Cardanova formula daje sljedeći izraz:

x = 3√ -1 + √-7 + 3√ -1 - √-7.         (**)

Sljedeća tablica govori nam da bi ta jednadžba trebala imati tri realna rješenja:
x -3 -2 -1 0 1 2 3
x3-6x+2 -7 6 7 2 -3 -2 11

Zaključujemo da je -3 < x1 < -2; 0 < x2 < 1; 2 < x3 < 3.



Za razliku od prethodnog primjera, matematičari 16. st. u početku nisu uspjeli doći do tih realnih brojeva, nego su samo imali izraz (**) u kojemu su morali vaditi korijene iz negativnih brojeva. Pred njima su se pojavila sljedeća pitanja:

  1. Kako iz izraza (*) i (**) rekonstruirati 3 realna rješenja jednadžbe?

  2. Kako treba na takvim izrazima izvesti operacije da bismo mogli računati uvjet uv = -p/3 ?

  3. Mogu li se u (**) i sličnim izrazima rješenja pripadajuće kubne jednadžbe zapisati bez korijena iz negativnih brojeva?
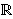Za odgovor na ta pitanja bilo je potrebno uvesti kompleksne brojeve i operacije s njima. Sustavna teorija kompleksnih brojeva prvi se put pojavila 1572. g. u Algebri talijanskog matematičara Raffaela Bombellia. Izrazi (*) i (**) zaista se mogu protumačiti tako da daju rješenje kubne jednadžbe. Kao što znate, kompleksni brojevi jesu brojevi oblika a + bi, a,b iz R, dok je imaginarna jedinica i izabrana tako da bude i2 = i 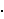* i = -1, tj. da bude rješenje jednadžbe x2 = -1. Tada se izraz (*) može zapisati kao

x = 3√i + 3√-i.         (*)'

Dakle, umjesto √-1 možemo staviti i. Budući da je -i također rješenje jednadžbe x2 = -1, umjesto √-1 mogli smo staviti -i. U (*) ništa se ne bi promijenilo (3√i prešao bi u 3√-i, a 3√-i u 3√i; zbroj bi ostao isti).

Izraz 3√i ima tri vrijednosti: z1 = √3/2 + 1/2 i, z2 = - √3/2 + 1/2 i, z3 = -i. Naime, ta su tri broja rješenja kubne jednadžbe z3 = i (provjerite).

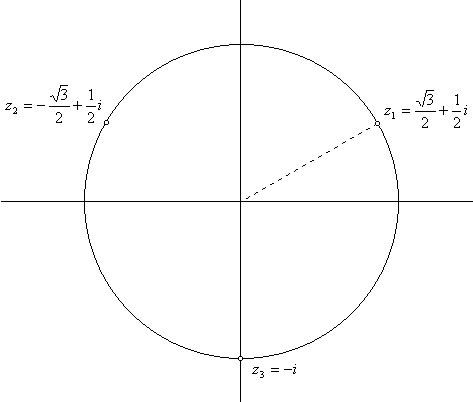
z_1,z_2,z_3

Slično tome, izraz 3√-i ima tri vrijednosti: w1 = i, w2 = - √3/2 - 1/2 i, w3 = √3/2 - 1/2 i.

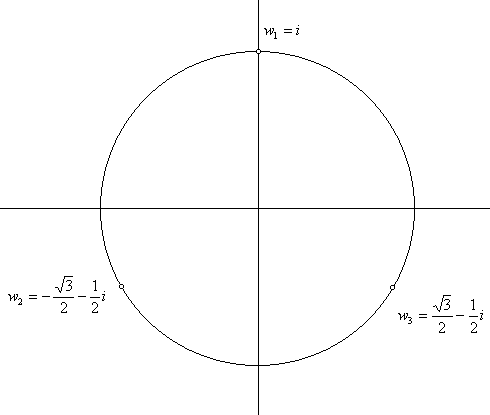
w_1,w_2,w_3

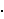Od 9 mogućih izbora zi, wi; i = 1,2,3 dobije se 9 mogućih vrijednosti izraza (*)'. Treba odabrati one za koje je uv = -p/3 = 1, tj. 3√i * 3√-i = 1.

Napomenimo da, iako kompleksni brojevi imaju svojstva analogna realnim brojevima, ima i nekih razlika. Osim one da se na kompleksne brojeve ne može proširiti relacija uređaja s 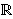R (tako da vrijede aksiomi uređenog polja), važna je razlika i u formulama √ab = √a √b; 3√ab = 3√a 3√b i sl. Naime, one se ne mogu doslovno primijeniti na kompleksne brojeve. Na primjer, kad bi bilo √(-1)(-1) = √-1 √-1, bilo bi √1 = i 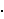* i, tj. 1 = -1 (Vidi: I.Gusić, Korjenovanje kompleksnih brojeva, Zbornik radova 1. kongresa matematike RH, 2000., 108-111). To se razrješava tako da bude √1 = {-1, 1}, √-1 = {i, -i}, dakle, skupovima brojeva. Prema tome, ako se radi s kompleksnim brojevima, √  nije jednoznačna funkcija nego ima dvije vrijednosti (izuzimajući činjenicu da je √0 = 0). Tada će zaista biti √(-1)(-1) = √-1 √-1 (na desnoj strani riječ je o umnošku skupova). Slično je 3√z za z 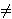<> 0 tročlan skup itd.

Vratimo se skupovima 3√i i 3√-i i uočimo da je z1w3 = z2w2 = z3w1 = 1 (a da su ostali međusobni umnošci različiti od 1). Zato izraz x = 3√i + 3√-i, uz uvjet 3√i 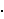* 3√-i = 1, ima tri vrijednosti: x1 = z1 + w3 = √3; x2 = z2 + w2 = - √3; x3 = z3 + w1 = 0. Upravo su to rješenja početne kubne jednadžbe x3 -3x = 0. Dakle, uz pravilno uvođenje kompleksnih korijena, formula x = 3√i + 3√-i može se protumačiti kao formula koja daje rješenja kubne jednadžbe x3 - 3x = 0.

Nekima niti to ne bi bio dovoljan razlog za uvođenje kompleksnih brojeva jer već znamo rješenje te jednadžbe. Razmotrimo zato jednadžbu x3 - 6x + 2 = 0, tj. izraz (**) x = 3√ -1 + √-7 + 3√ -1 - √-7. Taj izraz možemo pisati kao

x = 3√ -1 + i √7 + 3√ -1 - i √7,         (**)'

gdje je umnožak pribrojnika jednak 2. Pritom treba imati na umu sljedeće:

(i)   √7 je u (**)' običan realni drugi korijen iz 7, tj. pozitivan broj čiji je kvadrat jednak 7.

(ii)   3√  u oba pribrojnika ima tri vrijednosti, ali ćemo za svaku odabranu vrijednost 3√ -1 + i √7 imati točno jednu vrijednost od 3√ -1 - i √7 za koju će umnožak pribrojnika biti jednak 2.

Da bi to pokazali, matematičari 16. st. poslužili su se nečim što danas zovemo trigonometrijskim prikazom broja. Neka je z = -1 + √7 i; w = -1 -√7 i. Tada je z = 2√2 (cos fi + i sin fi), gdje je fi argument broja z.

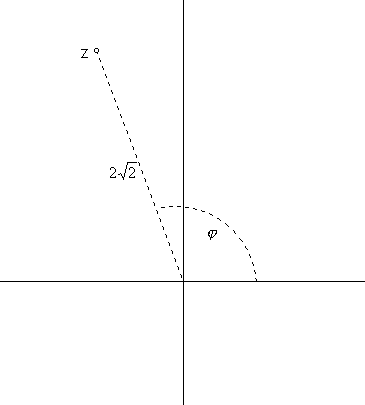
slika

Sada je 3√ -1 + i √7 = {z1, z2, z3},
z1 = √2 (cos (fi/3) + i sin (fi/3)),
z2 = √2 (cos (fi/3 + 120o) + i sin (fi/3 + 120o)),
z3 = √2 (cos (fi/3 + 240o) + i sin (fi/3 + 240o)).

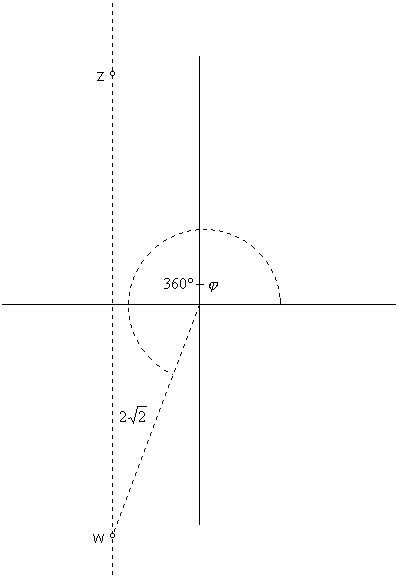
slika

Slično je 3√ -1 + i √7 = {w1, w2, w3},
w1 = √2 (cos (120o - fi/3) + i sin (120o - fi/3)),
w2 = √2 (cos (240o - fi/3) + i sin (240o - fi/3)),
w3 = √2 (cos (360o - fi/3) + i sin (360o - fi/3)).

Vidimo da je z1w3 = z2w2 = z3w1 = 2. Naime,

360o - (fi/3 + 120o) = 240o - fi/3,
360o - (fi/3 + 240o) = 120o - fi/3.

Zato su rješenja jednadžbe x3 -6x + 2 = 0 realni brojevi:
x1 = z1 + w3 = 2√2 cos (fi/3);
x2 = z2 + w2 = 2√2 cos (fi/3 + 120o);
x3 = z3 + w1 = 2√2 cos (fi/3 + 240o).

To su tri realna broja dobivena iz Cardanove formule pravilnom uporabom kompleksnih brojeva. Bez kompleksnih brojeva bilo bi gotovo nemoguće doći do tih rješenja. U tim rješenjima pojavljuje se kut fi koji se može eliminirati ovako: fi = 180o - arctg(√7) (naime, tg(180o - fi) = √7). Sada je

x1 = 2√2 cos (fi/3) = 2√2 cos (60o - arctg(√7) / 3) = 2√2 (1/2 cos (arctg(√7) / 3) + √3/2 sin (arctg(√7) / 3)),

itd.

Slično bi se dobilo za svaku kubnu jednadžbu x3 + px + q = 0, koja ima tri različita realna rješenja (odnosno za koju je D = q2 / 4 + p3 /27 < 0). Naime, za z = -q/2 + √D i, r = |z|, fi = arg(z) dobili bismo da je

x1 = 3√r cos (fi/3);
x2 = 3√r cos (fi/3 + 120o);
x3 = 3√r cos (fi/3 + 240o).

Eliminacijom kuta fi (fi = arctg(2√D/(-q)) za q < 0, fi = arctg(2√D/q) za q > 0 i fi = 90o za q = 0) dobili bismo da je

x1 = 2 3√r cos (arctg(2√D/(-q)) / 3),

itd. Vidimo da se rješenja mogu dobiti u ovisnosti o koeficijentima p,q jednadžbe, međutim u rješenjima sudjeluju transcendentne funkcije kosinus, sinus, arkus-tangens. Pitamo se mogu li se rješenja zapisati bez takvih funkcija, a i bez kompleksnih brojeva (kad su već realna)? Na primjer, mogu li se rješenja jednadžbe x3 - 6x + 2 = 0 zapisati samo pomoću korijena iz pozitivnih brojeva? Taj slučaj kubne jednadžbe, koji je najviše mučio matematičare 16. st., a i one kasnije, nazvan je nesvodljivim slučajem kubne jednadžbe. Kako smo vidjeli, zbog njega su uvedeni kompleksni brojevi i trigonometrijski prikaz. Tek je metodama Galoisove teorije iz 19. st. dan odgovor na gore postavljeno pitanje. Evo jedne varijante odgovora:

Neka je x3 + px + q = 0; p,q iz Q kubna jednadžba za koju je D < 0, koja nema racionalnog rješenja. Tada se rješenja te jednadžbe ne mogu zapisati pomoću realnih radikala (drugih, trećih ili nekih drugih korijena iz pozitivnih racionalnih brojeva).