
 |
Hrvatski matematički elektronski časopis math.e | |
| Broj 9 | ||
| http://www.math.hr/mathe/ |
Sadržaj:
1. Prvi problem o ortocentru
2. Drugi problem o ortocentru
3. Treći problem o ortocentru
4. Johnsonovi problemi s ortocentrom
5. Ortocentar na Internetu
6. Završne napomene
Literatura
Download
Ovo je neznatno proširena verzija dvaju članaka iz Matematičko-fizičkog lista istog naslova. U tim člancima prikazuju se tri teorema o ortocentru iz knjige "Trokut i kružnica" profesora Dominika Palmana [8], koji vrijede samo za šiljastokutne trokute. Pokazuje se da za tupokutne trokute treba izmijeniti jedan predznak u danim formulama da bi one postale točne i u ovom slučaju. Slične pogreške otkrivene su u poznatoj Johnsonovoj knjizi "Advanced Euclidean Geometry" [6] i u talijanskoj knjizi "Il Problema Geometrico - Dal compasso al Cabri" autora D'Ignazio i Suppa [5]. Nadopunjuje se i rješenje profesora Marića [7] problema o površini trokuta kome su poznate duljine stranica njegovog ortičkog trokuta. Završava se poboljšanjem nekih tvrdnji o ortocentru iz nekih dokumenata na Internetu. Ova verzija na mreži omogućava provjeru svih tvrdnji u priloženim Mathematica i Maple V bilježnicama (eng. notebooks), a slike su u boji i dinamičke jer su nacrtane u programu The Geometer's Sketchpad.
U knjizi "Trokut i kružnica" na 92. stranici u teoremu 11.10 tvrdi se sljedeće:
|
Teorem 1 (teorem 11.10 u [8]). Neka su D, E i F ortogonalne projekcije vrhova trokuta ABC na pravce njegovih stranica BC, CA i AB . Neka je R radijus opisane kružnice tog trokuta. Udaljenost |OH| između njegovog središta opisane kružnice O i ortocentra H dana je s
|
Očito je da formule (7a), (7b) i (7c) nisu ispravne jer bi iz njih slijedilo da udaljenost |OH| ne može biti veća od R (tj. da ortocentar trokuta uvijek leži unutar njemu opisane kružnice), što za tupokutne trokute ne vrijedi. U to se možemo uvjeriti i tako da na računalu u programu The Geometer's Sketchpad (ili kratko GSP) nacrtamo trokut ABC, točke D, E, F (nožišta visina), središte opisane kružnice O, ortocentar H, odredimo sve dužine koje se pojavljuju u gornjim formulama i izračunamo razlike (npr. |OH|2 + 2 · |AH| · |HD| − R2). Kada mičemo točke, nije točno da su razlike uvijek jednake nuli. Čim je trokut ABC tupokutan, dobivamo isti pozitivan broj za sve tri razlike (vidi sliku 1).
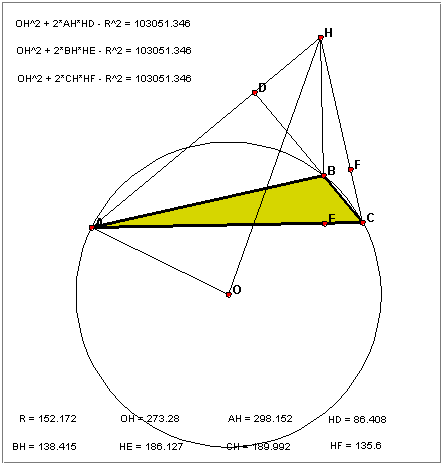
Kako se izvući iz ovih poteškoća? Moramo koristiti relativne mjerne brojeve dužina umjesto njihovih duljina (vidi stranicu 3 u [8]). Ako je [AB]ℓ oznaka za relativni mjerni broj dužine AB na orijentiranom pravcu ℓ, onda ispravljeni prvi dio teorema 11.10 iz [8] glasi ovako:
|
Teorem 2. (Popravljeni prvi dio teorema 11.10). Za udaljenost |OH| između središta opisane kružnice O i ortocentra H trokuta ABC vrijedi
|
Da dokažemo teorem 2, prvo ćemo dokazati sljedeću lemu.
|
Lema 1.
(a) Kut pri vrhu C veći je od 90° onda i samo onda ako je točka F između točaka A i B i ortocentar H je izvan dužine CF. (b) Ako je kut pri vrhu C veći od 90°, onda točka D leži između točaka A i H i točka E leži između točaka B i H. |
Dokaz. Odaberimo pravokutni koordinatni sustav tako da je A(0, 0), B(r(f+g), 0) i C((f 2−1)gr / (fg−1), 2fgr / (fg−1)). Parametri f i g su kotangensi polovica kutova A i B, a r je radijus upisane kružnice trokuta ABC. Primijetimo da su f, g i r povezani s duljinama stranica a, b i c ovako:
| f = | (a + b + c) (b + c − a) | , |
| 4 S |
| g = | (a + b + c) (a − b + c) | , |
| 4 S |
| r = | 2 S | , |
| a + b + c |
gdje je
| S = | √ (a + b + c) (b + c − a) (c + a − b) (a + b − c) | . |
| 4 |
Obrnuto,
| a = | r f (g 2 + 1) | , b = | r g (f 2 + 1) | , c = r (f + g). |
| f g − 1 | f g − 1 |
Ovakav odabir koordinata točaka i način dokazivanja uz pomoć računala, koji ćemo stalno koristiti, detaljno su objašnjeni u sljedećim člancima: [2], [3], [4] i [1].
(a) Koordinate točaka D, E, F, H i O su:
| ( | 4 g2 r(f + g) | , | 2 g r(f + g)(g 2 − 1) | ) | , |
| (g2 + 1)2 | (g2 + 1)2 |
| ( | r(f + g)(f 2 − 1)2 | , | 2f r(f + g)(f 2 − 1) | ) | , |
| (f 2 + 1)2 | (f 2 + 1)2 |
| ( | g r(f 2 − 1) | , 0 | ) | , |
| f g − 1 |
| ( | g r(f 2 − 1) | , | r(f 2 − 1)(g 2 − 1) | ) | , |
| f g − 1 | 2 (f g − 1) |
| ( | r(f + g) | , | r(f + g + f g − 1)(f + g − f g + 1) | ) | . |
| 2 | 4 (f g − 1) |
Odredimo realni broj w u kojem točka F dijeli dužinu AB. Drugačije rečeno, treba odrediti broj w tako da je (xA + w xB) / (1 + w) = xF i (yA + w yB) / (1 + w) = yF , gdje su xP i yP prva i druga koordinata točke P. Dobije se w = (b2 + c2 − a2) / (a2 + c2 − b2). Slično se pokazuje da ortocentar H dijeli dužinu CF u omjeru
| v = | 2 c2(a2 + b2 − c2) | . |
| (b2 + c2 − a2) (a2 + c2 − b2) |
Ako je kut pri vrhu C veći od 90°, onda je broj a2 + b2 − c2 negativan, a brojevi b2 + c2 − a2 i a2 + c2 − b2 su pozitivni. Dakle, broj w je pozitivan i točka F leži između A i B. S druge strane, broj v je negativan pa je ortocentar H izvan dužine CF.
Obrnuto, ako točka F leži između točaka A i B i ortocentar H je izvan dužine CF, onda je w > 0 i v < 0, što vodi do zaključka da je a2 + b2 − c2 < 0 pa je kut pri vrhu C veći od 90°.
(b) Ako je kut pri vrhu C veći od 90°, onda je broj a2 + b2 − c2 negativan, a brojevi b2 + c2 − a2 i a2 + c2 − b2 su pozitivni. Budući da točke D i E dijele dužine AH i BH u pozitivnim omjerima
| 16 S 2 |
| (c2 + a2 − b2) (c2 − a2 − b2) |
i
| 16 S 2 | , |
| (b2 + c2 − a2) (c2 − a2 − b2) |
zaključujemo da točka D leži između A i H i da točka E leži između B i H. □
| Lema 2. Ortocentar H je unutar kružnice opisane trokutu ABC, na njoj ili izvan nje, već prema tome je li taj trokut šiljastokutan, pravokutan ili tupokutan. |
Dokaz. Izračunamo li R2 − |OH|2, dobivamo
| (b2 + c2 − a2) (c2 + a2 − b2) (a2 + b2 − c2) | . |
| 16 S2 |
Dakle, ako je H unutar opisane kružnice, onda je R > |OH| pa je gornja razlika pozitivna, što je moguće jedino ako su sve tri zagrade u brojniku pozitivne, tj. ako je ABC šiljastokutan. Obrat očito također vrijedi.
Ako je H na opisanoj kružnici (tj. R = |OH|), onda jedna od zagrada u brojniku mora biti nula, što znači da je trokut pravokutan. To zaključivanje očigledno se može i obrnuti.
I na kraju, ako je ortocentar H izvan opisane kružnice, onda je |OH| > R. Tada brojnik gornjeg izraza mora biti negativan, što je moguće jedino ako je jedna od njegovih zagrada negativna, a ostale dvije su pozitivne. Dakle, tada je trokut tupokutan.
Obrnuto, ako je trokut ABC tupokutan, samo jedna od zagrada je negativna, a preostale dvije su pozitivne. Tada je |OH| > R pa ortocentar H leži izvan opisane kružnice. □
Dokaz teorema 2. Neka pravac visine AH siječe opisanu kružnicu, osim u točki A, još i u točki D0.
Ako je trokut ABC šiljastokutan, onda njegov ortocentar H leži unutar opisane kružnice. Potencija točke H s obzirom na tu opisanu kružnicu iznosi |AH| · |HD0| = R2 − |OH|2. Kako prema teoremu 11.1 u [8] vrijedi |HD0| = 2 · |HD|, gornja jednakost postaje
Stoga što u šiljastokutnom trokutu ortocentar H leži na dužini AD, sada vrijedi |AH| = [AH]AH i |HD| = [HD]AH, što odmah povlači relaciju (7a*).
Ako je trokut ABC pravokutan, onda se ortocentar nalazi u jednom od vrhova i dvije od točaka D, E i F također su u tom vrhu, a središte opisane kružnice je u polovištu nasuprotne stranice i vrijedi |OH| = R. Zbog toga su produkti 2 · [AH]AH · [HD]AH, 2 · [BH]BH · [HE]BH i 2 · [CH]CH · [HF]CH jednaki nuli i formule (7a*) - (7c*) vrijede.
Ako je trokut ABC tupokutan, onda je ortocentar H izvan opisane kružnice. Dakle, njegova potencija s obzirom na opisanu kružnicu iznosi |AH| · |HD0| = |OH|2 − R2. Kao i malo prije za šiljastokutne trokute, lijeva strana je 2 · |AH| · |HD|. S druge strane, prema lemi 1, [AH]AH = |AH| i [HD]AH = −|HD| pa opet dobivamo formulu (7a*). Formule (7b*) i (7c*) dobivaju se slično. □
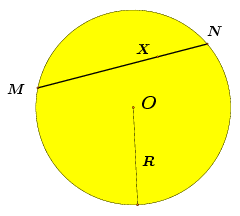
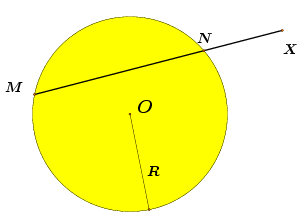
Napomena. (a) Ovo je zapravo dokaz iz Palmanove knjige, malo modificiran. No, ako primijetimo da je uvijek
(tj. da za "modificiranu" potenciju točke X u odnosu na kružnicu radijusa R sa središtem u točki O na slici 2 uvijek vrijedi [NX]MN · [XM]MN = R2 − |OX|2), onda se Palmanov dokaz može doslovno prepisati ovako:
i
zajedno daju relaciju (7a*) i to vrijedi bez obzira na kutove trokuta ABC. Dakle, lema 1 nam nije potrebna!
(b) Drugi način popravka prvog dijela teorema 1 je da stavimo
| | |HO|2 − R2| | = |AH| · |HD| = |BH| · |HE| = |CH| · |HF|. |
| 2 |
Mana tog oblika je to što s njime nemamo eksplicitni izraz za udaljenost |HO| ortocentra od središta opisane kružnice.
(c) Uz pomoć računala lako se može dokazati sljedeći djelomični obrat formule iz (b). Za točku P ravnine različitu od vrhova A, B i C trokuta ABC, presjeke pravaca AP, BP i CP redom s pravcima BC, CA i AB označavamo s aP, bP i cP.
Teorem 3.
Neka trokut ABC nije pravokutan. Njegov
ortocentar H je jedina točka P
ravnine različita od vrhova A, B
i C za koju vrijedi
|
U prethodnom teoremu nije dovoljno tražiti samo da je
jer za trokut u kojem je f = 2, g = 5, r = 1 postoje čak tri točke različite od ortocentra H(5/3, 4) za koje vrijedi gornja dvostruka jednakost. Najjednostavnija takva točka je
| ( | 256 + 20 m + 18 m2 | , m | ) | , |
| 33 |
za m = k/54 − 2129/(18k) i k = (388800 + 3√45746138067)⅓.
U sljedećem teoremu 11.11 iz knjige [8] piše:
|
Teorem 4. (teorem 11.11 u [8]) Neka su D, E i F ortogonalne projekcije vrhova trokuta ABC na pravce njegovih stranica BC, CA i AB. Neka je R radijus opisane kružnice tog trokuta, a r radijus njemu upisane kružnice. Udaljenost |IH| između njegovog središta upisane kružnice I i ortocentra H dana je s
|
Očito je da formule (9a), (9b) i (9c) nisu ispravne jer bi iz njih slijedilo da udaljenost |IH| ne može biti veća od r√2, što za tupokutne jednakokračne trokute kod kojih je ortocentar udaljen od vrha tupog kuta za više od r√2 ne vrijedi. U to se možemo uvjeriti i tako da na računalu u Geometer's Sketchpadu nacrtamo trokut ABC, točke D, E, F, zatim središte upisane kružnice I i ortocentar H, a onda odredimo sve dužine koje se pojavljuju u gornjim formulama i izračunamo razlike (npr. |IH|2 + |AH| · |HD| − 2 r2). Kada pomičemo točke, nije točno da su te razlike uvijek jednake nuli. Čim je trokut ABC tupokutan, gornje razlike nisu nula, već su sve tri jednake istom pozitivnom broju (vidi sliku 3).
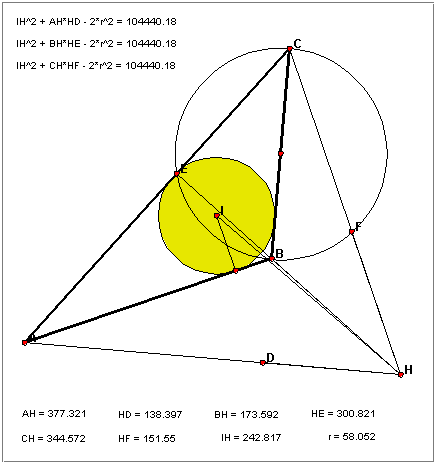
Ako se prisjetimo načina kako smo se izvukli iz problema u prvom teoremu, dolazimo na ideju da ispravak prvog dijela formuliramo ovako:
|
Teorem 5. (Popravljeni prvi dio teorema
11.11 iz [8]). Udaljenost |IH| između središta upisane kružnice I i ortocentra H trokuta ABC dana je s
|
Dokaz teorema 5. Po teoremu 2 imamo
| = [CH]CH · [HF]CH = | R2 − |OH|2 | . |
| 2 |
Dakle, dovoljno je pokazati
| 2 |IH|2 − |OH|2 + R2 = 4 r2. | (*) |
Budući da (uz oznake kao u lemi 1) središte upisane kružnice I ima koordinate (fr, r), a koordinate središta opisane kružnice O i ortocentra H znamo iz dokaza prvog dijela leme 1, lako izračunamo, "pješke" ili uz pomoć računala, da je
| |IH|2 = | r2 M1 | , |
| 4 (f g − 1)2 |
| |OH|2 = | r2 M2 |
| 16 (f g − 1)2 |
i
| R2 = | r2 M3 | , |
| 16 (f g − 1)2 |
gdje su M1, M2 i M3 polinomi f 4g4 − 2f 4g2 − 4f 3g3 − 2f 2g4 + f 4 + 4f 3g + 12f 2g2 + 4fg3 + g4 − 2f 2 − 20fg − 2g2 + 9, 9 + 9f 4g4 − 14f 4g2 − 32f 3g3 + 9f 4 − 14f 2g4 + 32f 3g + 36f 2g2 + 32fg3 + 9g4 − 14f 2 − 32fg − 14g2 i (f 2 + 1)2(g2 + 1)2. Jednakost (*) je posljedica relacije
koju lako dokazujemo jer se radi o jednostavnim operacijama s polinomima. □
Napomena. (a) Drugi način popravka prvog dijela teorema 4 je da stavimo | |HI|2 − 2r2| = |AH| · |HD| = |BH| · |HE| = |CH| · |HF|. Loša strana tog oblika je to što nemamo eksplicitni izraz za udaljenost |HI| ortocentra od središta upisane kružnice.
(b) Na računalu se lako dokazuje ovaj obrat formule iz (a). Za pojašnjenje oznaka aP, bP i cP vidi napomenu iza dokaza teorema 2.
| Teorem 6. Ortocentar H je jedina točka P ravnine trokuta ABC za koju vrijedi trostruka jednakost | |PI|2 − 2r2| = |AP| · |P aP| = |BP| · |P bP| = |CP| · |P cP|. |
I naredni Teorem 11.12 knjige [8] ima slične poteškoće. U njemu se tvrdi sljedeće:
|
Teorem 7 (teorem 11.12 u [8]).
Zbroj udaljenosti ortocentra H od vrhova danog trokuta ABC jednak je dvostrukom zbroju promjera opisane i upisane kružnice toga trokuta,
|
Prvi dio iskaza teorema sadrži pogrešku jer je promjer kružnice jednak dvostrukom njezinom polumjeru. Dakle, trebalo bi zapravo reći: "…jednak je zbroju promjera opisane i upisane kružnice tog trokuta" (tj. treba izbaciti riječ "dvostrukom"). Pogrešna tvrdnja izražena formulom (12) dana je u knjizi [8] pod nazivom Carnotov teorem već ranije na 78. stranici.
Ako na računalu u Geometer's Sketchpadu nacrtamo trokut ABC, središta I i O upisane i opisane kružnice, ortocentar H, odredimo sve dužine koje se pojavljuju u formuli (11) i izračunamo razliku |HA| + |HB| + |HC| − 2 (R + r), vidimo da ona nije uvijek jednaka nuli kada mičemo točke. Čim je trokut ABC tupokutan, gornja razlika je različita od nule (vidi sliku 4).
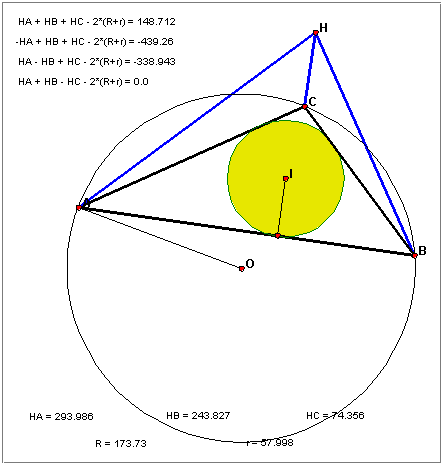
Promotrimo li malo pažljivije dobivene brojeve u slučaju da je neki kut tup, vidimo da gornju razliku treba smanjiti, što nas navodi na ideju da ispravak formuliramo ovako:
|
Teorem 8. (Popravljeni teorem 11.12 iz
[8]).
(a) Trokut ABC nije tupokutan onda i samo onda ako je zbroj udaljenosti ortocentra H od vrhova jednak zbroju promjera opisane i upisane kružnice tog trokuta,
|
Dokaz teorema 8. Kako u trokutu najviše jedan kut može biti veći ili jednak kutu od 90°, možemo pretpostaviti da su kutovi A i B šiljasti. Zato u odabiru koordinata pomoću veličina f, g i r (kotangensi kuteva A/2 i B/2 i polumjer upisane kružnice) možemo uzeti da je f > 1 i g > 1. Lako se izračuna da je
| |HA| = | r(f 2 − 1) (g2 + 1) | , |
| 2 (f g − 1) |
| |HB| = | r (f 2 + 1) (g2 − 1) | , |
| 2 (f g − 1) |
| |HC| = | r (f g + f + g − 1) |f g − f − g −1| |
| 2 (f g − 1) |
i
| R = | r (f 2 + 1) (g2 + 1) | . |
| 4 (f g − 1) |
(a) Ako trokut ABC nije tupokutan, onda je prema dolje dokazanoj lemi 3 udaljenost |HC| jednaka
| r (f g + f + g − 1) (f + g − f g + 1) | . |
| 2 (f g − 1) |
Sada se uvrštavanjem gornjih prikaza lako provjeri da je |HA| + |HB| + |HC| = 2(R + r).
Obrnuto, ako se u jednakost |HA| + |HB| + |HC| = 2(R + r) za |HA|, |HB| i R uvrste gornje vrijednosti i riješi po |HC|, dobije se
| |HC| = | r (g + f + f g − 1) (f + g − f g + 1) | . |
| 2 (f g − 1) |
Usporedbom s gornjim izrazom za |HC| vidimo da izraz fg − f − g − 1 nije pozitivan pa prema lemi 3 slijedi da kut C nije tup (tj. da trokut ABC nije tupokutan).
Budući da su zbog jednakosti |AH| = 2 · |OA'|, |BH| = 2 · |OB'| i |CH| = 2 · |OC'| (vidi teorem 11.5 u [8]) tvrdnje (b) i (d) očigledno ekvivalentne tvrdnjama (a) i (c), mi ćemo još samo dokazati tvrdnju (c).
(c) Ako kut C nije šiljast, onda je prema lemi 3 udaljenost |HC| jednaka
| r (f g + f + g − 1) (f g − f − g − 1) | . |
| 2 (f g − 1) |
Sada odmah slijedi |HA| + |HB| − |HC| = 2(R + r).
Obrnuto, ako se u jednakost |HA| + |HB| − |HC| = 2(R + r) za |HA|, |HB| i R uvrste gornje vrijednosti i riješi po |HC|, dobije se
| |HC| = | r (g + f + f g − 1) (f g − f − g − 1) | . |
| 2 (f g − 1) |
Kako je |HC| ≥ 0, vidimo da je fg − f − g − 1 ≥ 0. Ako je fg − f − g − 1 = 0, onda je c2 = a2 + b2 pa je prema Pitagorinom teoremu kut C pravi. Ako je fg − f − g − 1 > 0, onda prema lemi 3 slijedi da je kut C tup (tj. da je trokut ABC tupokutan). Dakle, u svakom slučaju, kut C nije šiljast. □
| Lema 3. Trokut ABC ima tupi kut u vrhu C onda i samo onda ako je izraz ctg(A/2)·ctg(B/2) − ctg(A/2) − ctg(B/2) − 1 pozitivan. |
Dokaz. Gornji trigonometrijski izraz zapravo je fg − f − g − 1 koji, kada se prikaže pomoću duljina stranica, postaje
| c (4S + c2 − (a + b)2) | . |
| 2 S (a + b − c) |
To će biti pozitivno onda i samo onda ako je 4S > (a + b + c) (a + b − c). Kako je
vidimo da je gornji izraz pozitivan onda i samo onda ako je c2 − a2 − b2 > 0, što je očito ekvivalentno s tvrdnjom da je kut C tup. □
Greška iz teorema 11.12 knjige [8] pojavljuje se i u mnogo starijoj i u svijetu poznatijoj knjizi Rogera A. Johnsona [6], gdje je formula (12) na stranici 190 dana u tvrdnji f. i formula (11) na stranici 191 opet kao tvrdnja f. Na toj 191. stranici ima još dosta pogrešaka pa ćemo sada opisati kako ih popraviti.
|
Teorem 9.
(Popravak tvrdnje b. iz
[6] str.
191). (a) Trokut ABC nije tupokutan onda i samo onda ako je opseg njegovog ortičkog trokuta DEF jednak kvocijentu dvostruke površine i polumjera opisane kružnice trokuta ABC, tj. |EF| + |FD| + |DE| = 2S/R. (b) Kut C u trokutu ABC nije šiljast onda i samo onda ako vrijedi |EF| + |FD| − |DE | = 2S/R. |
Dokaz. Kao i u dokazu teorema 8, možemo uzeti da je f > 1 i g > 1. Lako se izračuna
| |EF| = | r f (f 2 − 1) (g2 + 1) | , |
| (f 2 + 1) (f g − 1) |
| |FD| = | r g (f 2 + 1) (g2 − 1) | , |
| (g2 + 1) (f g − 1) |
| |DE| = | r (f + g) (f g + f + g − 1) |f g − f − g − 1| |
| (f 2 + 1) (g2 + 1) |
i
| S = | f g r2 (f + g) | . |
| f g − 1 |
(a) Ako trokut ABC nije tupokutan, onda je prema lemi 3 duljina stranice |DE| ortičkog trokuta jednaka
| r (f + g) (f g + f + g − 1) (f + g − f g + 1) | . |
| (f 2 + 1) (g2 + 1) |
Sada se uvrštavanjem gornjih prikaza lako provjeri da je |EF| + |FD| + |DE| = 2S/R.
Obrnuto, ako se u jednakost |EF| + |FD| + |DE| = 2S/R za |EF|, |FD| R i S uvrste gornje vrijednosti i riješi se po |DE|, dobije se
| |DE| = | r (f + g) (g + f + f g − 1) (f + g − f g + 1) | . |
| (f 2 + 1) (g2 + 1) |
Usporedbom s gornjim izrazom za |DE| vidimo da izraz fg − f − g − 1 nije pozitivan pa prema lemi 3 slijedi da kut C nije tup (tj. da trokut ABC nije tupokutan).
(b) Ako kut C nije šiljast, prema lemi 3 stranica |DE| je jednaka
| r (f + g) (f g + f + g − 1) (f g − f − g − 1) | . |
| (f 2 + 1)(g2 + 1) |
Sada odmah slijedi |EF| + |FD| − |DE| = 2S/R.
Obrnuto, ako se u jednakost |EF| + |FD| − |DE| = 2S/R za |EF|, |FD|, R i S uvrste gornje vrijednosti i riješi se po |DE|, dobije se
| |DE| = | r (f + g) (g + f + f g − 1) (f g − f − g − 1) | . |
| (f 2 + 1) (g2 + 1) |
Kako je |DE| ≥ 0, vrijedi fg − f − g − 1 ≥ 0. Ako je fg − f − g − 1 = 0, onda je c2 = a2 + b2, pa je prema Pitagorinom teoremu kut C pravi. Ako je fg − f − g − 1 > 0, onda prema lemi 3 slijedi da je kut C tupi (tj. da je trokut ABC tupokutan). Dakle, u svakom slučaju, kut C nije šiljast. □
|
Teorem 10.
(Popravak tvrdnje c. iz [6],
str. 191).
(a) Trokut ABC nije tupokutan onda i samo onda ako je udaljenost nožišta ortogonalnih projekcija točke D na pravce CA i AB jednaka polovici opsega njegovog ortičkog trokuta DEF. (b) Kut A u trokutu ABC nije šiljast onda i samo onda ako je udaljenost nožišta ortogonalnih projekcija točke D na pravce CA i AB jednaka (|FD| + |DE| − |EF|)/2. |
|
Teorem 11.
(Popravak tvrdnje d. iz [6], str. 191).
(a) Trokut ABC nije tupokutan onda i samo onda ako je |AD| · |BE|· |CF| = S (|EF| + |FD| + |DE|) (tj. produkt duljina visina tog trokuta jednak je produktu njegove površine i opsega njegovog ortičkog trokuta DEF). (b) Kut A u trokutu ABC nije šiljast onda i samo onda ako je |AD| · |BE| · |CF| = S (|FD| + |DE| − |EF|). |
U dijelu g. na stranici 191 u [6] razmatra se polumjer ρ upisane kružnice ortičkog trokuta DEF. Prvo se tvrdi da je ρ = |HD| cosA = 2R cosA cosB cosC, što očigledno nije istinito kada je kut A tup jer je tada cosA negativan.
Što je onda |HD| · |cosA| kada je kut A tup? Taj produkt nije polumjer upisane kružnice ortičkog trokuta DEF, već polumjer ρa njegove pripisane kružnice nasuprot vrha D. Tada je vrh A središte upisane kružnice trokuta DEF, a ne ortocentar H (koji je to kada je kut A šiljast i koji za tupi A prelazi u središte njegove D-pripisane kružnice).
Dalje se tvrdi da je |AH| · |HD| = 2R ρ. Opet je to točno samo kada trokut ABC nije tupokutan. Ako je trokut ABC tupokutan, onda je |AH| · |HD| = 2R ρa. Slične tvrdnje vrijede za produkte |BH| · |HE| i |CH| · |HF|.
Slijedi Johnsonova tvrdnja da je omjer površina ortičkog trokuta DEF i osnovnog trokuta ABC jednak ρ/R. To isto vrijedi samo za trokute koji nisu tupokutni. Ako je trokut ABC tupokutan, taj omjer jednak je ρa/R, ρb/R ili ρc/R, već prema tome koji je kut trokuta ABC tup.
Interesantno je da istu pogrešku nalazimo i u zadatku 52(c) na strani 273. talijanske knjige [5] iz 2001. godine, kada su programi za dinamičku geometriju poput Cabri, Cindarella i Geometer's Sketchpad već dosta rasprostranjeni. I prethodni zadatak 52(b) tamo pogrešno tvrdi da za sve trokute vrijedi
| |AH| · |AD| + |BH| · |BE| + |CH| · |CF| = | a2 + b2 + c2 | . |
| 2 |
Ova formula je također istinita samo za trokute koji nisu tupokutni, a ako je, na primjer, kut C tup, onda ona glasi:
| |AH| · |AD| + |BH| · |BE| − |CH| · |CF| = | a2 + b2 + c2 | . |
| 2 |
I na kraju, Johnson izvodi zaključak da je a2 + b2 + c2 = 8R2 + 4ρR. Kao i gore, ta formula je istinita samo za trokute koji nisu tupokutni. Ako trokut ABC ima tupi kut, desna strana mora biti 8R2 − 4ρaR, 8R2 − 4ρbR ili 8R2 − 4ρcR, ovisno o tome koji je kut trokuta ABC tup.
Zatim dolazi tvrdnja h. koja glasi: |AH|2 + |BH|2 + |CH|2 = 4 R2 − 4 ρ R.
I ovdje je za tupokutne trokute desna strana zapravo 4R2 + 4ρaR, 4R2 + 4ρbR ili 4R2 + 4ρcR, već prema tome koji je kut trokuta ABC tup.
Postoji još jedan način kako ukloniti neke od Johnsonovih poteškoća. Bolje je s ρ označiti (zajedničku) udaljenost ortocentra H od pravaca EF, FD i DE. Onda je ρ = |HD| · |cosA| = 2R · |cosA cosB cosC|, |AH| · |HD| = 2Rρ i omjer površina trokuta DEF i ABC jednak |DEF| / |ABC| = ρ/R, bez ikakvih ograničenja na trokut ABC.
Primijetimo da se nedavno u članku [7] analizira rješavanje problema određivanja površine trokuta ABC kojemu ortički trokut DEF ima stranice 13, 14 i 15. Izvodi se formula |DEF|/|ABC| = ρ/R i primjećuje da ona vrijedi jedino za trokute koji nisu tupokutni. Posljednji paragraf glasi ovako:
"Kod tupokutnog trokuta su nožišta dviju visina, kao i ortocentar, izvan trokuta i očito ništa od navedenog ne vrijedi (jer smo u svim dokazima koristili da je ortički trokut dio polaznog trokuta, što sada nije). Može se pokazati da i u ovom slučaju postoje zanimljivi odnosi među elementima tih dvaju trokuta. Ali, o tome možda drugom prigodom."
Nažalost, ne primjećuje se da tvrdnja može biti istinita iako neka posebna metoda njezinog dokazivanja nije provediva i da navedene napomene o posebnosti tupokutnih trokuta imaju za posljedicu da razmatrani problem, pored rješenja |ABC| = 1365/4, ima još tri rješenja. To su |ABC| = 130, |ABC| = 455/4 i |ABC| = 195/2. Sva četiri rješenja su prikazana na slici 5.
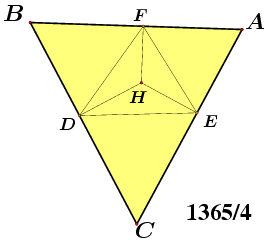
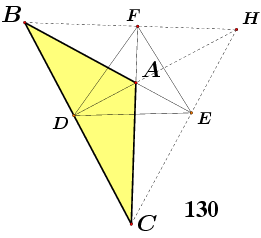
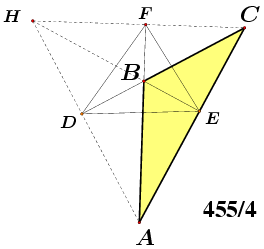
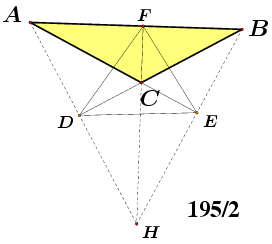
U programu Maple V naš dokaz prvo odredi rješenje f = 2, g = 7/4 i r = 4 sistema
| 13 = | r f (g2 + 1) | , |
| f g − 1 |
| 14 = | r g(f 2 + 1) | , |
| f g − 1 |
i onda te vrijednosti uvrsti u koordinate središta upisane kružnice I(fr, r) i triju pripisanih kružnica
| Ae | ( | (f + g) f g r | , | (f + g) g r | ) | , |
| f g − 1 | f g − 1 |
| Be | ( | r (f + g) | , | r (f + g) f | ) |
| 1 − f g | f g − 1 |
i Ce(gr, −fgr). Na kraju, koristi se formula
| (b − c) x + (c − a) y + (a − b) z |
| 2 |
za površinu trokuta kojemu vrhovi imaju koordinate (x, a), (y, b) i (z, c). Tražene površine su |AeBeCe| = 1365/4, |IBeCe| = 130, |AeICe| = 455/4 i |AeBeI| = 195/2.
Ako na Internetu tražimo dokumente koji sadrže riječ "Orthocenter" (engleski za ortocentar), pojavljuje se više desetaka tisuća mogućnosti. Neke od njih su iz zubarstva, ali one iz matematike uglavnom ponavljaju samu definiciju ortocentra kao presjeka visina i/ili opisuju najjednostavnija njegova svojstva.
Na primjer, na adresi
autor ponavlja pogrešnu tvrdnju da je opseg ortičkog trokuta 2S/R (vidi teorem 9).
Ugledna kolekcija sadržaja iz matematike MathWorld u sklopu službene web stranice Wolfram Researcha (proizvođača programa Mathematica), koju uređuje Eric W. Weisstein, na adresi
navodi neke od rezultata koje smo razmatrali, ali samo uz pretpostavku da je promatrani trokut šiljastokutan.
I na kraju, Jim Wilson daje dva rezultata o sumi omjera nekih dužina vezanih uz ortocentar i najavljuje da oni ovise o tome kakve kutove ima trokut. Mi ih ovdje dajemo u nešto poboljšanom obliku kao sljedeća dva teorema. Dokaze prepuštamo čitateljima za vježbu.
|
Teorem 12. (a) Trokut ABC nije tupokutan onda i samo onda ako je
(b) Trokut ABC ima tupi kut u vrhu C onda i samo onda ako je
|
|
Teorem 13.
(a) Trokut ABC nije tupokutan onda i samo onda ako je
(b) Trokut ABC ima tupi kut u vrhu C onda i samo onda ako je
|
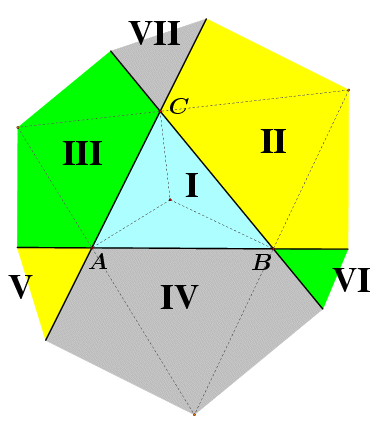
Wilson također spominje da zadnji teorem ima poopćenje kada se promatraju omjeri |PPa|/|AD|, |PPb|/|BE| i |PPc|/|CF|, gdje su Pa, Pb i Pc nožišta okomica iz točke P na pravce BC, CA i AB. Naš sljedeći teorem još je jedno poboljšanje u kojem ne moramo imati okomice. U njegovoj formulaciji koristimo sedam područja na koje tri pravca koja nisu kopunktalna dijele ravninu (vidi sliku 6).
|
Teorem 14.
Neka točka P nije vrh trokuta
ABC, a pravci AP, BP i CP
sijeku pravce BC, CA i AB u
točkama U, V i W. Za
točku Q različitu od točke
P neka paralele kroz Q s pravcima
AP, BP i CP sijeku pravce
BC, CA i AB u točkama
X, Y i Z.
(a) Ako je točka Q u području I, onda je
(b) Ako je točka Q u području II, onda je
(c) Ako je točka Q u području III, onda je
(d) Ako je točka Q u području IV, onda je
(e) Ako je točka Q u području V, onda je
(f) Ako je točka Q u području VI, onda je
(g) Ako je točka Q u području VII, onda je
|
Dokaz. Ako trokut ABC ima koordinate vrhova kao i u dokazu teorema 8 i ako je P(p, q) i Q(u, v), onda je lako naći koordinate točaka U, V, W, X, Y i Z i izračunati
| |QX| | = | |2 g u + (g2 − 1) v − 2 g r (f + g)| | , |
| |AU| | 2 g r (f + g) |
| |QY| | = | |−2 f u + (f 2 − 1) v| |
| |BV| | 2 f r (f + g) |
i
| |QZ| | = | v (f g − 1) | . |
| |CW| | 2 f g r |
Primijetite da koordinati p i q točke P u tim izrazima nema.
Budući da su funkcije u brojnicima tih kvocijenata jednadžbe pravaca stranica trokuta, pažljivom analizom predznaka njihovih vrijednosti lako se potvrđuju relacije (a) - (g). □
Poteškoće u teoremima 11.10, 11.11 i 11.12 iz [8] otkrivene su na predavanjima autora u sklopu kolegija "Matematika računalom" na studiju matematike na Prirodoslovno-matematičkom fakultetu Sveučilišta u Zagrebu, gdje studenti uče kako koristiti računala u rješavanju matematičkih problema. Poteškoće iz Johnsonove knjige otkrivene su jednostavnom provjerom što o sličnim temama pišu drugi jer sam pretpostavljao da su pogreške naslijeđene. Primjeri profesora Marića i Wilsona pokazuju da tupokutni trokuti ipak nisu zanemareni, iako su malo problematičniji od šiljastokutnih i pravokutnih trokuta.
Dakle, knjige i članke iz matematike (a pogotovo iz geometrije) treba pažljivo čitati i svaku tvrdnju detaljno analizirati i po mogućnosti za svaku nacrtati slike u nekom od programa za dinamičku geometriju da se vidi kako se tvrdnja ponaša za različite položaje promatranih objekata.
Isto tako, knjige i članke pišu samo ljudi pa je prirodno očekivati da ponekad imaju grešaka.
| [1] | M. Bator, Z. Čerin, M. Čulav, Analitička geometrija ravnine računalom, Matematičko-fizički list (Zagreb), 54 (2003./2004.), br. 1, 23-31. |
| [2] | Z. Čerin, S. Vlah, Rješavanje zadataka računalom, Matka (Zagreb), 10 (2001./2002.), br. 39, 198-202. |
| [3] | Z. Čerin, S. Vlah, Primjeri upotrebe računala kod rješavanja zadataka, Matematičko-fizički list (Zagreb), 52 (2001./2002.), br. 4, 254-261 |
| [4] | Z. Čerin, S. Vlah, Još jedno rješenje drugog zadatka na 42. MMO 2001 g., Matematičko-fizički list (Zagreb), 53 (2002./2003.), br. 1, 55-56. |
| [5] | I. D'Ignazio, E. Suppa, Il Problema Geometrico - Dal compasso al Cabri, Interlinea Editrice, Teramo, 2001. |
| [6] | R. A. Johnson, Advanced Euclidean Geometry, Dover Publications, New York, 1960. |
| [7] | Anđelko Marić, Analiza jednog geometrijskog problema, Bilten seminara iz matematike za nastavnike-mentore, 13. državni susret, Trogir 5.- 8. svibnja 2004., HMD, 86 - 95. |
| [8] | Dominik Palman, Trokut i kružnica, Element, Zagreb 1994. |
1. Prvi problem o ortocentru
2. Drugi problem o ortocentru
3. Treći problem o ortocentru
4. Johnsonovi problemi s ortocentrom
5. Ortocentar na Internetu
6. Završne napomene
Literatura
Download