Hrvatski matematički elektronski časopis math.e
	http://www.math.hr/~mathe/

Rješenje zadatka iz rubrike Matematika u literaturi (6. broj časopisa)

ZADATAK:

Da vidimo: četiri puta pet jest dvanaest, a četiri puta šest jest trinaest, a četiri puta sedam je – joj meni! Ako budem ovako dalje, nikad neću doći do dvadeset!

Pretpostavimo li da je Alisina računica točna, ona zaista nikada neće doći do dvadeset! Vaš je zadatak pokušati obrazložiti zašto. Da biste došli do odgovora, morate pretpostaviti da su Alisine tvrdnje istinite ili, bolje rečeno, ustanoviti KADA su one istinite. Tada ćete, nastavivši niz koji je Alisa započela, shvatiti zašto nikada neće doći do dvadeset!

RJEŠENJE:

Kako bismo otkrili zašto Alisa neće doći do dvadeset, moramo ustanoviti kada su njezine tvrdnje točne. Dakle, kada će četiri puta pet zaista biti dvanaest? Očito ne ako su brojevi zapisani u dekadskom brojevnom sustavu!

Brojevni sustav u kojem četiri puta pet jest dvanaest lako se pronalazi: označimo li s B bazu traženog sustava, samim time što koristimo znamenke 4 i 5 znamo da je B 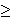 6.

Nadalje vrijedi: 4_(B) = 4B⁰ = 4 i 5_(B) = 5B⁰ = 5 (bazu 10 nećemo označavati).

Kako je 45 = 20, preostaje još samo pronaći onaj brojevni sustav u kojem se broj 20 zapisuje znamenkama 12 (12_(B) = 20).

Za bazu tog sustava vrijedit će jednakost 12_(B) = 2B⁰ + 1B¹ = 2 + B = 20 pa zaključujemo da je traženi brojevni sustav onaj s bazom 18.

Dakle, 4₍₁₈₎5₍₁₈₎ = 12₍₁₈₎.

Analogno, četiri puta šest bit će trinaest kada su brojevi napisani u sustavu s bazom 21:

4(21) = 4210 = 4,

6(21) = 6210 = 6,

13(21) = 3210 + 1211 = 3 + 21 = 24.

Nastavimo li niz, svaka će sljedeća jednakost vrijediti za sustav kojem je baza za 3 veća od prethodne:

	47 = 14	(baza 24),
	48 = 15	(baza 27),
	49 = 16	(baza 30),
	4A = 17	(baza 33),
	4B = 18	(baza 36),
	4C = 19	(baza 39),
i napokon	4D = 1A	(baza 42).

Nešto trivijalnije obrazloženje ponudio je najpoznatiji Alisin analitičar, Martin Gardner, u svom djelu The Annotated Alice: Alisa nije mogla doći do dvadeset jer su se tada u engleskim školama koristile tablice množenja do dvanaest pa Alisa nije znala množiti s trinaest (slovo D u zadnjoj jednakosti koja bi trebala rezultirati s dvadeset).

Napomenimo još i da ova obrazloženja ne potječu od samog autora, tako da postoji mogućnost da je riječ o slučajnostima te da je Alisa zaista govorila besmislice. No, uzmemo li u obzir da je, kao što već možda i znate, Alisin tvorac matematičar i logičar (iza pseudonima Lewis Carroll krije se Charles L. Dodgson, oxfordski profesor čiju biografiju možete pročitati ovdje), mogućnost da je sve ovo tek puka slučajnost čini se malo vjerojatnom. Koji bi matematičar čiste savjesti ispisao niz netočnih aritmetičkih jednakosti, a da ne dozvoli mogućnost da one imaju smisla? A ako ste još uvijek skeptični i smatrate da se u jednoj dječjoj knjizi ne mogu nalaziti ovako složene matematičke "mozgalice", pozivamo vas da ponovo uhvatite "Alisu" u ruke i uvjerite se kako knjiga obiluje duhovitim i inteligentnim dosjetkama. Za potpun doživljaj predlažemo čitanje u originalnoj verziji, kako vam ne bi promakle brojne igre riječima (čitav tekst možete pronaći ovdje).