Hrvatski matematički elektronski časopis math.e
	http://www.math.hr/~mathe/

Heuristički algoritmi za 0-1 problem naprtnjače

Anamari Nakić

Sadržaj:

1. Uvod

Navikli smo vjerovati da računalo može riješiti probleme brže i točnije od nas samih, dovoljno mu je pokazati kako. Jedan od poznatih matematičkih zadataka jest i problem trgovačkog putnika. Prilično ga je jednostavno opisati, način pronalaženja rješenja brzo se nametne, ali koliko bi vremena računalu trebalo da riješi ovaj problem - to je već drugo pitanje. Dakle, trgovački putnik mora obići n gradova tako da završi u onom u kojem je i počeo, te da svaki grad (osim prvoga) obiđe samo jednom. Svaka dva grada povezuje jedna cesta tako da je mnogo različitih načina na koje naš trgovački putnik može posjetiti sve gradove, no njegov je cilj prijeći što manje kilometara i vratiti se kući što prije. Prvo što nam pada na pamet jest izračunati duljine svih mogućih puteva koji zadovoljavaju uvjete i odabrati onaj najkraći. Za n gradova takvih je puteva n!. Tako bismo za 5 gradova morali izračunati duljine 5! = 1 * 2 * 3 * 4 * 5 = 120 različitih puteva. Za 100 gradova taj broj približno iznosi ogromnih 10¹⁵⁸. Radi boljeg shvaćanja koliko je to teško izračunati, evo male usporedbe: znanstvenici tvrde da se starost svemira kreće između 12 i 20 milijardi godina. Ako pretpostavimo da je svemir star 12 milijardi godina, znači da je nastao prije 10¹⁶ sekundi. Da smo pokrenuli računalo u trenutku njegova nastanka i kad bi ono radilo sve te godine brzinom od otprilike milijardu operacija u sekundi, sada bismo imali rješenje. Pa, možemo reći da bi računalo došlo do rješenja brže od prosječnog čovjeka, ali prosječan čovjek nikako ne bi mogao dočekati kraj izvršavanja programa (a vjerojatno ni prosječno računalo). Ipak, moguće je da smo odabrali pogrešan algoritam. Možda možemo pronaći algoritam koji ne generira baš sve moguće putove, već u nekoj ranijoj fazi računa prepoznaje one koji nisu optimalni pa ih ne uzima u obzir. Takvi su algoritmi poznati, no oni su eksponencijalne složenosti kao i naš prvi algoritam i to je još uvijek prevelik zalogaj za današnja računala.

2. Heuristički algoritmi

U ovom je slučaju ipak bolje izračunati neko približno rješenje nego oporučno budućim generacijama ostaviti da čekaju da vaše računalo završi s radom. Iako je naša želja pronaći optimalno rješenje, to je ponekad preteško pa bismo se zadovoljili i nekim dopustivim rješenjem koje ne mora nužno biti optimalno, ali zadovoljava sve uvjete problema. Vrlo često metode približnog računanja imaju čvrstu matematičku pozadinu koja svjedoči o njihovoj pouzdanosti neovisno o ulaznim podacima. U isto vrijeme daju i ocjenu konvergencije pa uvijek možemo biti svjesni koliko smo blizu ( ili daleko ) optimalnom rješenju. No, ponekad je iz rezultata očito da nije daleko od optimalnog, ali (još uvijek) nije dokazano koliko je metoda dobra te koliko smo blizu najboljem rješenju i nema garancije da će račun dati dobre rezultate za različite ulazne parametre. Takve metode nazivaju se heurističkima.

Naziv heuristički algoritam koristi se za opisivanje algoritma koji se bazira na heuristici. Takvi su algoritmi obično iterativni. Potragu za rješenjem počinju nekim trivijalnim dopustivim rješenjem problema koje je često daleko od optimalnog. Pri svakoj iteraciji modificiraju trenutno rješenje kako bi došli što bliže optimalnom. Heuristika se koristi prilikom odabira parametara za iduću iteraciju unutar algoritma kao i prilikom odabira konstanti koje se koriste tijekom algoritma. Heuristički algoritmi baziraju se na različitim strategijama: tako neki pronalaze ideju oponašajući kaljenje metala (eng. simulated annealing), neki penjanje uz planinu (eng. hill-climbing), a neki evolucijske procese.

Osim heurističkih, postoje i aproksimacijski algoritmi koji se koriste u iste svrhe. Razlika između ovih dviju vrsta algoritama u tome je što za aproksimacijske algoritme postoje neke matematičke ocjene konvergencije, tj. možemo odrediti koliko ćemo se dobro približiti optimalnom rješenju. Za heurističke algoritme nema matematičkog dokaza da rade dobro, ali se u primjenama pokazuju zadovoljavajućim, a mogu biti brži od aproksimacijskih algoritama.

Konkretno, uzmimo da bi za obilazak 5 gradova putnik morao prijeći najmanje 768 kilometara. Heuristički algoritam mogao bi dati za rješenje baš 768, ali i 1000 i 1048 ili neki drugi broj, ovisno o ulaznim parametrima. Čak štoviše, prilikom ponovnog izvođenja algoritma (programa) s istim parametrima mogli bismo dobiti sasvim drugo rješenje. Nema garancije da ćemo dobiti dobar rezultat, ali nakon nekoliko pokretanja programa šanse su velike da ćemo doći do zadovoljavajuće kilometraže.

3. Tabu algoritam

Osnovna ideja ovog tipa heurističkog algoritma jest zamijeniti dopustivo rješenje X novim, najboljim rješenjem Y iz njegove okoline, koje je također dopustivo. Treba biti pažljiv jer moglo bi se dogoditi da u sljedećem koraku zamijenimo Y s X pa bismo se počeli vrtjeti u krug, što nikako ne želimo. Zato se izgrađuje "tabu-lista" u kojoj se nalaze neka rješenja koja algoritam ne smije odabrati u sljedećem koraku. U tabu-listi ne nalaze se sva dopustiva rješenja koja je algoritam u nekom koraku posjetio, već samo ona posjećena u zadnjih L iteracija (uobičajeno je L = 10). Za potpuno onemogućavanje ciklusa, L bi trebao biti jako velik, no tada ne bi bilo mnogo dozvoljenih odabira i bilo bi ih teško naći. Time bi se program usporio, što je u suprotnosti s onim što se heurističkim algoritmima nastoji postići: dopušta se lošiji rezultat, ali se omogućava veća brzina izvođenja programa.

4. Simulirano kaljenje

Algoritam simuliranog kaljenja, kao i tabu algoritam, omogućava bijeg iz lokalno optimalnog rješenja (koje ne mora nužno biti i globalno optimalno), a bazira se na metodi oplemenjivanja metala koja se naziva kaljenjem i koristi se već 7000 godina. Proces se sastoji od 3 faze: zagrijavanja na visoku temperaturu, zadržavanja na toj temperaturi i zatim hlađenja, obično na sobnu temperaturu. Polaganim hlađenjem inducira se promjena kristalne rešetke metala tako da njezina energija postaje najmanja moguća. Tako metali postaju čvršći. Hlađenje je potrebno obaviti vrlo pažljivo: ako se ohladi prebrzo, može doći do pucanja metala, a potrebno je i neko vrijeme kako bi došlo do potrebnih transformacija u molekularnoj strukturi metala.

U općenitom slučaju naša je želja maksimalizirati neku funkciju P, tj. pronaći takav X da je P(X) maksimalna. Ova metoda aktualno dopustivo rješenje X zamjenjuje nekim njemu bliskim dopustivim rješenjem Y ako je P(Y) 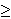P(X). No, ponekad je i u slučaju kada je P(Y) < P(X) dopušteno X zamijeniti s Y: ako za slučajno generirani r 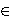[0,1] vrijedi

X će se zamijeniti s Y. Vjerojatnost da se dopustivo rješenje X zamijeni s Y kada je P(Y) < P(X) iznosi e^{(P(Y) - P(X)) / T}. Na taj način algoritam neće zaglaviti u lokalnom minimumu.

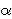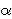Kako ova metoda simulira hlađenje, kontrolna varijabla koja oponaša padanje temperature (T) iznimno je važna, a njezina je početna vrijednost T₀ > 0. Tijekom izvođenja programa varijabla T smanjuje se prema određenom rasporedu hlađenja. Uobičajeno je da se nakon svake iteracije T promijeni prema pravilu T : = T, 0 < < 1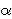 ( konstanta). U početku će vjerojatnost zamjene biti velika pa će biti više zamjena X i Y, no sa svakom iteracijom ta će vjerojatnost padati i zamjene koje smanjuju vrijednost funkcije P postajat će rjeđe.

5. 0-1 problem naprtnjače

Spremajući se za put, vjerojatno se uvijek trudite ponijeti što manje stvari, a opet dovoljno da imate sve što vam može zatrebati. To vjerojatno činite odoka, imate već iskustva u pakiranju. No, u nekom skladištu ponekad je teško procijeniti koju robu staviti u kamion tako da bude maksimalno popunjen, a da zarada nakon istovara bude najveća moguća uz postojeća ograničenja (npr. veličina kamiona ili ukupna težina tereta). Optimalno je rješenje, kao i kod problema trgovačkog putnika, za velik broj predmeta (uz memorijska i procesorska ograničenja današnjih računala) teško pronaći pa ćemo se poslužiti heurističkim algoritmima.

0-1 problem naprtnjače jedan je od poznatijih ( i jednostavnijih ) problema iz klase NP. Neke njegove inačice koristile su se u kriptiranju. Jedna od njih je i problem zbroja podskupa: u danom skupu prirodnih brojeva potrebno je odrediti postoji li podskup kojem je zbroj elemenata jednak nekom zadanom broju. No, vratimo se našem originalnom problemu i zapišimo ga formalnije kako bismo ga mogli lakše koristiti u programiranju.

Ako je dano n predmeta (y₀,..., y_n-1), svaki od njih s težinom w_i i cijenom p_i , i = 0,...n-1, potrebno je utvrditi koje je predmete moguće odabrati tako da suma njihovih težina ne prelazi zadani M, a da je njihova ukupna vrijednost maksimalna. Tada je rješenje n-torka X = (x₀,..., x_n-1) 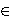{0,1}ⁿ, takva da je

i

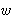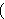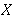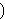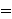
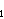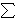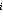
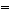
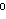
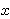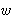
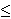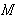
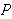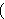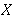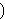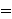
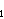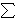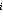
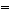
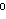
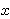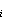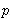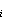
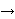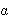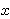
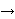
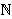
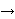
Uređenu n-torku interpretiramo ovako: ako smo i-ti predmet stavili u ruksak, x_i = 1, u suprotnom x_i = 0. Funkcija 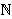w:{0,1}ⁿ naziva se težinska funkcija i njome računamo ukupnu sumu težina odabrane n-torke, dok je P :{0,1}ⁿ funkcija profita.

Ovaj problem može se egzaktno riješiti metodom iscrpljujućeg pretraživanja prostora dopustivih rješenja (riječ je o tzv. backtracking algoritmu, detaljnije o tome možete pročitati u [3]).

Slijede dva heuristička algoritma za 0-1 problem naprtnjače.

6. Simulirano kaljenje za 0-1 problem naprtnjače

Neka je X = (x₀,..., x_n-1) neko dopustivo rješenje te neka je j slučajno izabran broj, 0 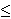j 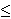n-1 . Tada se novo rješenje Y = (y₀,..., y_n-1) dobije tako da

Primijetite da je Y dopustivo rješenje ako x_j = 1 ili ako je x_j = 0 i w(X) + w_j 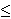M. Sada je očito da je

Pretpostavimo sada da je Y dopustivo rješenje (w(Y) 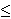M). Ako je x_j = 0, onda je P(X) < P(Y) i X će biti zamijenjen s Y. Ako je pak x_j = 1, onda je P(Y) < P(X) te vrijedi P(Y) - P(X) = -p_j. Vjerojatnost da će X tada biti zamijenjen s Y iznosi e^{-p_j / T}.

Najčešće se za početnu vrijednost uzima X = (0,...,0). Još je potrebno odrediti parametre T₀, 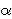i c_max. Pravilo ne postoji: nakon nekoliko pokušaja s različitim vrijednostima varijabli pokaže se koje vrijednosti daju najbolja rješenja. Parametar T₀ se odabire tako da je vjerojatnost zamjene na početku algoritma visoka. Ako se želi da temperatura sporo pada, 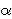mora biti blizu 1 ( 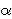= 0.995, 0.999, 0.9999). U suprotnom, što je 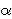manji, temperatura će brže padati. Preporučljivo je da broj iteracija bude veći od 1000 (c_max 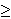1000). Ovaj algoritam nema ocjene koliko se možemo približiti rješenju. Za neke će ulazne podatke raditi loše, pa je potrebno malo eksperimentirati s parametrima kako bi se dobila efikasna verzija programa.

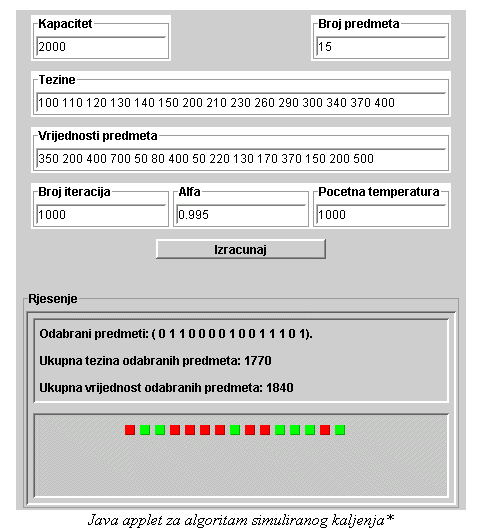
Dodatak: Pseudokod za algoritam simuliranog kaljenja za 0-1 problem naprtnjače

7. Tabu algoritam za 0-1 problem naprtnjače

Kao i kod algoritma simuliranog kaljenja, novo rješenje Y dobiveno iz X razlikovat će se od X samo u jednoj koordinati: y_i = 1 - x_i. Način na koji ćemo odabirati koordinatu i neće biti slučajan, već ćemo pokušati povećati profit što je više moguće. Pokazalo se da je bolje gledati omjere profita i težine p_i/w_i nego samo profite. Ovo je, dakle, naša strategija:

1. Ako postoji barem jedan indeks i koji nije na tabu-listi takav da je x_i = 0, x_i i takav da se može promijeniti x_i u 1, a da je suma težina svih odabranih predmeta ne prelazi kapacitet ruksaka (M), odaberemo onaj indeks i za koji je vrijednost p_i/w_i maksimalna, te promijenimo x_i u 1.
2. Ako nijedan takav i ne postoji, promotrimo sve indekse i takve da je x_i = 1 i i nije na tabu-listi. Među njima odaberemo indeks i takav da je vrijednost p_i/w_i minimalna i promijenimo x_i u 0.

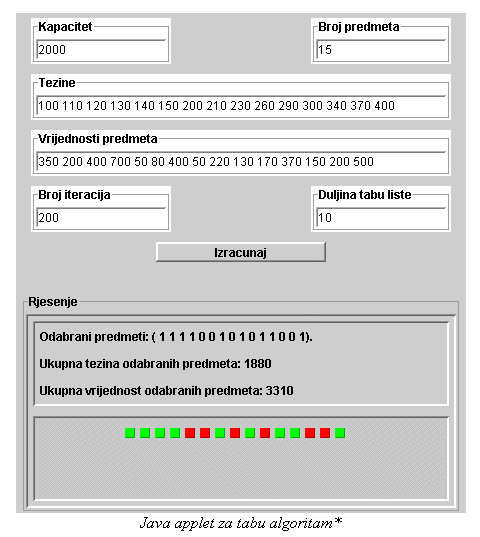
Dodatak: Pseudokod tabu algoritma za 0-1 problem naprtnjače

8. Klasa NP

I problem trgovačkog putnika i 0-1 problem naprtnjače spadaju u klasu NP. Jedno od svojstava problema te klase jest da još uvijek nije poznato postoji li upotrebljivi algoritam polinomijalne složenosti koji pronalazi optimalno rješenje. Eksponencijalni algoritmi svakako postoje, ali lako ćete se uvjeriti da oni za veće instance problema nisu praktični.

Pronalazak bržih algoritama za NP-teške probleme jedno je od velikih otvorenih pitanja suvremene matematike. O težini tog problema i njegovoj važnosti svjedoči podatak da je za njegovo rješenje slavni Clay institut ponudio milijun dolara. U pokušajima da se ovaj problem riješi (naravno, iz ljubavi prema znanosti, nikako prema novcu), postignuti su mnogi važni rezultati i ovo je jedno od matematičkih područja koje se razvija velikom brzinom. Stoga požurite, jer milijun dolara možda čeka upravo vas. Dovoljno je odgovoriti na jednostavno pitanje:

Zadaci

1. Isprobajte applet za algoritam simuliranog kaljenja sa sljedećim ulaznim podacima. 15 predmeta ima redom težine:
   70 73 77 80 82 87 90 94 98 106 110 113 115 118 120

   te odgovarajuće vrijednosti profita:

   135 139 149 150 156 163 173 184 192 201 210 214 221 229 240 .
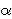   Dozvoljeni kapacitet je 750. Broj iteracija neka bude 1000, 5000, 20000, a neka varira između 0,999 i 0,9999. Početna temperatura neka je T₀ = 1000. Algoritam izvršite dvadesetak puta za svaki varijabilni parametar algoritma. Primijetite da rješenja nisu uvijek ista. Maksimalni profit je 1458, a optimalna n-torka (1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1). Pronalazi li algoritam i optimalna rješenja? Učinite isto s appletom za tabu algoritam. Pripazite da tabu-lista ne bude preduga (dovoljno L < 10) te da broj iteracija ne bude prevelik (dovoljno c_max < 1000). Koji algoritam daje vrijednosti bliže optimalnom rješenju?
   
   
2. Isprobajte applet za tabu algoritam sa sljedećim ulaznim podacima. 24 predmeta ima redom težine:
   382745 799601 909247 729069 467902 44328 34610 698150
   823460 903959 853665 551830 610856 670702 488960 951111
   323046 446298 931161 31385 496951 264724 224916 169684

   te odgovarajuće vrijednosti profita:

   825594 1677009 1676628 1523970 943972 97426 69666 1296457
   1678693 1902996 1844992 1049289 1252836 1319836 953277 2067538
   675367 853655 1826027 65731 901489 577243 466257 369261 .
   Dozvoljeni kapacitet je 6404180. Broj iteracija neka bude 200, 500, 1000, a L =1,..., 8. Algoritam izvršite dvadesetak puta za svaki varijabilni parametar algoritma. Primijetite da rješenja nisu uvijek ista. Maksimalni profit je 13549094, a optimalna n-torka (1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1). Pronalazi li algoritam i optimalna rješenja? Učinite isto s appletom za algoritam simuliranog kaljenja. Možete odabrati parametre iz prethodnog zadatka. Koji algoritam daje vrijednosti bliže optimalnom rješenju?

Bibliografija

[1] M. Sipser: Introduction to the Theory of Computation, PWS, Boston, 1997.

[2] D.L. Kreher, D.R. Stinson: Combinatorial Algorithms - Generation, Enumeration and Search, CRC Press, Boca Raton, 1999.

[3] R.Manger, M.Marušić: Strukture podataka i algoritmi, PMF-Matematički odjel, Zagreb, 1999.

[4] R. Sedgewick: Algorithms in C, Addison-Wesley, Reading, 1990.