
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://www.math.hr/~mathe/ |
Iracionalne jednadžbe i nejednadžbe
Nikola Dmitrović
Napomena: Na slikama koje se pojavljuju u ovom članku crvena boja predstavlja graf lijeve, a plava desne strane (ne)jednadžbe.
Za početak promotrimo slučaje koji se u konačnici mogu svesti na oblik
√f(x) = g(x). (1.1)
Poštujući svojstva funkcije drugi korijen, moramo prvo postaviti uvjete za rješenja jednadžbe (1.1). Određivanje uvjetâ, između ostalog, predstavlja nalaženje područja definiranosti, kako funkcije drugi korijen, tako i ostalih funkcija koje se javljaju u jednadžbi. Evidentno, prvi uvjet za rješenje jednadžbe (1.1) jest da ono mora zadovoljavati f(x) ≥ 0. Međutim, to nije dovoljno. Naime, htjeli bismo jednadžbu kvadrirati da se riješimo drugog korijena. No, tada moramo paziti na neinjektivnost kvadriranja, odnosno na činjenicu da za c > 0 dva broja x zadovoljavaju x2 = c, ali se samo jedan od njih (onaj pozitivni) ima pravo zvati √c (naravno, za c = 0 jedino je rješenje 0, pa nema tih problema). To znači da prije kvadriranja moramo osigurati da obje strane (konkretno desna, za koju želimo da bude jednaka nekom korijenu) jednadžbe budu nenegativne. Dakle, drugi uvjet za rješenje glasi g(x) ≥ 0.Nakon kvadriranja dobivamo jednadžbu
f(x) = (g(x))2, (1.2)
koja je uz dane uvjete ekvivalentna s (1.1). Uočimo da nam je, uz (1.2), uvjet f(x) ≥ 0 nepotreban. Naime, sva rješenja koja dobijemo zadovoljavat će (1.2), pa će za njih biti f(x) = (g(x))2 ≥ 0. Dakle:
√f(x)
= g(x)
 g(x) ≥ 0
&
f(x) = (g(x))2.
g(x) ≥ 0
&
f(x) = (g(x))2.
2n√f(x) = g(x)
 g(x) ≥ 0 &
f(x) = (g(x))2n.
g(x) ≥ 0 &
f(x) = (g(x))2n.
2n+1√f(x) =
g(x)
 f(x) = (g(x))2n+1.
f(x) = (g(x))2n+1.
Primjer 1. Riješimo jednadžbu √1 - x = 5 + x.
Rješenje:
√1 - x = 5 + x
 5 + x ≥ 0 &
1 - x = 25 + 10x + x2
5 + x ≥ 0 &
1 - x = 25 + 10x + x2
 x ≥ -5 &
x2 + 11x + 24 = 0
x ≥ -5 &
x2 + 11x + 24 = 0
 x ≥ -5 &
(x = -3
x ≥ -5 &
(x = -3
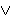 x = -8)
x = -8)
 x = -3
x = -3
Primjer 2. Riješimo jednadžbu √x2 - 3x + 3 + √(x2 - 36) = x - 1.
Rješenje:
√x2 -
3x + 3 + √(x2
- 36) = x - 1
 x - 1 ≥ 0 &
x2 -
3x + 3 + √x2 -
36 = x2 - 2x + 1
x - 1 ≥ 0 &
x2 -
3x + 3 + √x2 -
36 = x2 - 2x + 1
 x ≥ 1 &
√x2 - 36
= x - 2
x ≥ 1 &
√x2 - 36
= x - 2
 x ≥ 1 &
x ≥ 2 &
x2 - 36 =
x2 - 4x + 4
x ≥ 1 &
x ≥ 2 &
x2 - 36 =
x2 - 4x + 4
 x ≥ 2 &
4x = 40
x ≥ 2 &
4x = 40
 x = 10
x = 10
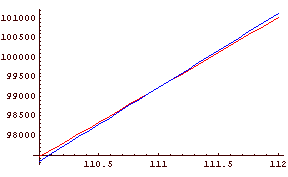
Pri rješavanju iracionalnih jednadžbi možemo se služiti i grafičkom metodom. Ona ne daje egzaktna rješenja, već nam može pomoći u razlučivanju pravih od "fiktivnih" rješenja.
Primjer 3. Riješimo jednadžbu
√( √2x + 3 + √4x - 3 ) = √6 (1.3)
Rješenje: Obje strane jednadžbe su nenegativne, pa možemo pristupiti kvadriranju. Stoga je jednadžba (1.3) ekvivalentna jednadžbi√2x + 3 + √4x - 3 = 6 (1.4)
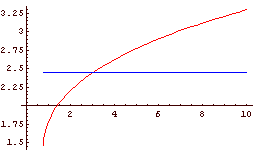
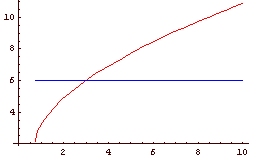
√2x + 3 √4x - 3 = 18 - 3x (1.5)
Sada nije dovoljno provjeriti uvjet na nenegativnost desne strane i kvadrirati (1.5) jer radikandi mogu biti negativni. Iz uvjeta nenegativnosti radikanadaSada, uzevši u obzir da je 18 - 3x ≥ 0 i kvadrirajući (1.5), dobivamo:
(2x + 3)(4x - 3) = (18 - 3x)2
&
18 - 3x ≥ 0 &
x ≥ 3/4
 8x2 + 6x - 9 =
324 - 108x + 9x2
&
x ≤ 6 &
x ≥ 3/4
8x2 + 6x - 9 =
324 - 108x + 9x2
&
x ≤ 6 &
x ≥ 3/4
 x2 - 114x + 333 = 0
&
x
x2 - 114x + 333 = 0
&
x
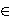 [3/4,6]
[3/4,6]
 (x = 3
(x = 3
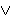 x = 111) &
x
x = 111) &
x
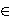 [3/4,6]
[3/4,6]
 x = 3.
x = 3.
u + v = c & u2 + v2 = a + b.
Ako je jednadžba oblika √a + f(x) + √b + f(x) = c, (c ≠ 0), ona se supstitucijama u = √a + f(x) i v = √b + f(x) svodi na:
u + v = c &
u2 - v2 =
a - b
 u + v = c &
(u + v)(u - v) = a - b
u + v = c &
(u + v)(u - v) = a - b
 u = (c2 + a - b)/2c
&
v = (c2 - a + b)/2c.
u = (c2 + a - b)/2c
&
v = (c2 - a + b)/2c.
√x + 5 + √20 - x = 7 (1.6)
Rješenje: Supstitucije glase: u = √x + 5, v = √20 - x i uz njih vrijedi:
u + v = 7 &
u2 + v2
= 25 &
x + 5 ≥ 0 & 20 - x ≥ 0
 u + v = 7 &
u2 + v2
= 25 &
x
u + v = 7 &
u2 + v2
= 25 &
x 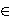 [-5,20]
[-5,20]
 u2 + v2
= 25 &
u = 7 - v &
x
u2 + v2
= 25 &
u = 7 - v &
x 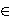 [-5,20]
[-5,20]
 u2 - 7u + 12 = 0
&
u = 7 - v &
x
u2 - 7u + 12 = 0
&
u = 7 - v &
x 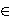 [-5,20]
[-5,20]
 {u,v} = {3,4} &
x
{u,v} = {3,4} &
x 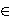 [-5,20]
[-5,20]
 ((u,v) = (3,4)
((u,v) = (3,4)
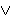 (u,v) = (4,3)) &
x
(u,v) = (4,3)) &
x 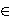 [-5,20]
[-5,20]
 (x = 4
(x = 4
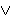 x = 11) &
x
x = 11) &
x 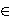 [-5,20]
[-5,20]
 x = 4
x = 4
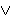 x = 11.
x = 11.
Primjer 5. Riješimo u skupu R nejednadžbu:
√x2 - 4x + 3 ≥ 2 - x. (2.1)
Rješenje: Ako ovu nejednadžbu kvadriramo, dobit ćemo sljedeću situaciju:
x2 - 4x + 3 ≥
4 - 4x + x2
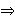 3 ≥ 4,
(2.2)
3 ≥ 4,
(2.2)
a = b
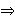 f(a) = f(b),
f(a) = f(b),
a < b
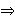 f(a) < f(b),
f(a) < f(b),
x2 - 4x + 3 ≥ 0,
dobivamo x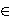
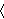 -
-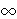 , 1]
, 1]
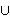 [3, +
[3, +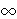
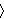 .
Dakle, konačan skup rješenja je presjek tih dvaju skupova,
tj. x
.
Dakle, konačan skup rješenja je presjek tih dvaju skupova,
tj. x 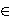 [3, +
[3, +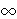
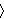 .
.
Imajući u vidu gornji primjer, iracionalne nejednadžbe u kojima se nepoznanica javlja pod korijenom možemo podijeliti u 4 podgrupe.
 f(x) ≥ 0 &
g(x) > 0 &
f(x) < (g(x))2n
f(x) ≥ 0 &
g(x) > 0 &
f(x) < (g(x))2n
 ( f(x) ≥ 0 &
g(x) < 0 )
( f(x) ≥ 0 &
g(x) < 0 )
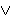 ( g(x) ≥ 0
&
f(x) > (g(x))2n )
( g(x) ≥ 0
&
f(x) > (g(x))2n )
 g(x) > 0 &
f(x) > (g(x))2n
g(x) > 0 &
f(x) > (g(x))2n
 ( g(x) < 0 &
f(x) ≥ 0 )
( g(x) < 0 &
f(x) ≥ 0 )
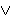 ( g(x) > 0
& f(x) ≥ 0 &
f(x) < (g(x))2n )
( g(x) > 0
& f(x) ≥ 0 &
f(x) < (g(x))2n )
√x2 + 3x + 2 < 1 + √x2 - x + 1 (2.3)
Rješenje: Odredimo uvjete za definiranost funkcija koje se pojavljuju u zadatku. Primijetimo da je drugi radikand uvijek pozitivan jer mu je vodeći koeficijent pozitivan, dok mu je diskriminanta ((-1)2 - 4 = -3) negativna. Za prvi radikand uvjet je:
x2 + 3x + 2 ≥ 0
 x
x 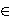
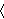 -
-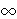 , -2]
, -2]
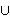 [-1, +
[-1, +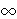
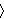 .
.
√x2 - x + 1
> 2x &
x 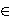
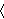 -
-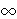 , -2]
, -2]
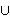 [-1, +
[-1, +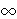
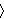

( 2x < 0 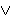 ( 2x ≥ 0 &
x2 - x + 1 >
4x2 )) &
x
( 2x ≥ 0 &
x2 - x + 1 >
4x2 )) &
x 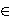
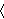 -
-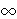 , -2]
, -2]
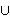 [-1, +
[-1, +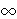
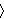

( x < 0 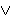 ( x ≥ 0 &
x
( x ≥ 0 &
x 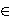
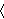 (-1 - √13) / 6, (-1 + √13) / 6
(-1 - √13) / 6, (-1 + √13) / 6
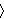 ))
&
x
))
&
x 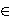
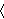 -
-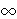 , -2]
, -2]
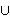 [-1, +
[-1, +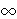
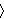

x 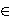
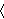 -
-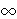 , -2]
, -2]
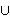 [-1,
(√13 - 1) / 6
[-1,
(√13 - 1) / 6
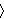 .
.
√4 - √(1 - x) - √2 - x > 0 (2.4)
Rješenje: Prvo provjerimo uvjete za definiranost korijenâ koji se pojavljuju u nejednadžbi.
2 - x ≥ 0
 x ≤ 2
x ≤ 2
4 - √1 - x ≥ 0
 √1 - x ≤ 4
√1 - x ≤ 4
 0 ≤ 1 - x ≤ 16
0 ≤ 1 - x ≤ 16

-15 ≤ x ≤ 1
(2.5)
(2.4)
 √4 - √(1 - x) >
√2 - x
√4 - √(1 - x) >
√2 - x
 4 - √1 - x >
2 - x & (2.5)
4 - √1 - x >
2 - x & (2.5)

√1 - x <
x + 2 & (2.5)
 1 - x < x2 + 4x + 4
& x + 2 ≥ 0 & (2.5)
1 - x < x2 + 4x + 4
& x + 2 ≥ 0 & (2.5)

x2 + 5x + 3 > 0 &
x ≥ -2 & (2.5)

x 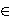
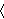 -
-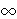 ,
(-5 - √13) / 2
,
(-5 - √13) / 2
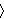
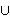
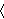 (-5 + √13) / 2,
+
(-5 + √13) / 2,
+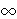
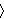 &
x ≥ -2 & (2.5)
&
x ≥ -2 & (2.5)

x 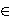
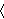 (-5 + √13) / 2, 1
(-5 + √13) / 2, 1
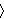 .
.
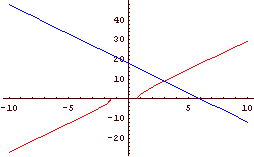
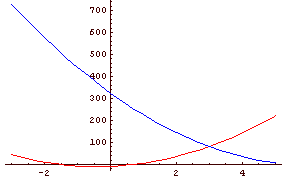
√x2 + 3x + 2 < 1 + √x2 - x + 1
Slika 1: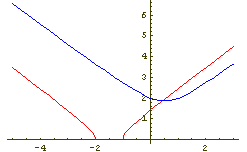 Slika 2:
Slika 2: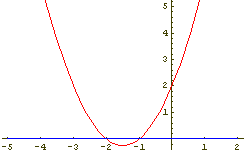
Slika 3: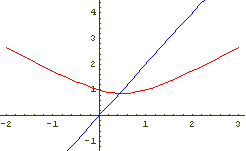 Slika 4:
Slika 4: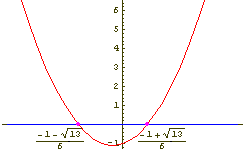
√4 - √(1 - x) - √2 - x > 0
Slika 5: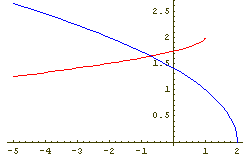 Slika 6:
Slika 6: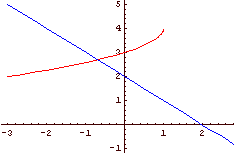
Slika 7: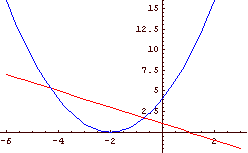 Slika 8:
Slika 8: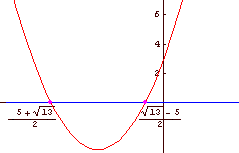
Primjer 8.
√2x + x + lg(x) - 7 > √2x + 3x2 + lg(x) - 66 (2.6)
(lg(x) je oznaka za logaritam od x po bazi 2, tj. lg(x) = log2 x = log(x)/log(2))Rješenje: Kad bismo slijedili postupak iz prethodnih primjera, to bi zahtijevalo (pri određivanju uvjeta za definiranost korijena) rješavanje nejednadžbi poput
2x + x + lg(x) ≥ 7, (2.7)
što baš i nije lako - osim ako se sjetimo nečega u čemu nam Graphitude može pomoći. Naime, ako nacrtamo graf lijeve strane nejednadžbe (2.7) (recimo s parametrima xmin=0, xmax=5, ymin=0, ymax=10), vidimo da se on uspinje. Ako u tom svjetlu gledamo (2.7), odmah vidimo da je funkcija na lijevoj strani strogo rastuća, kao zbroj tri strogo rastuće funkcije, pa je injekcija. To ima za posljedicu da je rješenje odgovarajuće jednadžbe jedinstveno, pa ga je dovoljno pogoditi. Tu opet možemo upotrijebiti Graphitude. Na grafu vidimo da prolazi kroz točku (2,7), dakle (jedino) rješenje jednadžbe je x = 2. Budući da je funkcija na lijevoj strani strogo rastuća, slijedi da je rješenje nejednadžbe (2.7) dano s x ≥ 2. Da bi lg(x) bio definiran, mora biti x > 0, pa je i radikand desne strane u (2.6) rastuća funkcija od x. Analogno (crtajući graf s parametrima xmin=0, xmax=5, ymin=-60, ymax=60) dobivamo za uvjet na desnoj strani x ≥ 4. Dakle, ukupni uvjet je x ≥ 4, i uz taj uvjet smijemo kvadrirati (2.6) (obje strane su nenegativne). Kvadriranjem se "neugodni" članovi ponište, te ostaje kvadratna nejednadžba3x2 - x - 59 < 0,
kojoj je rješenje x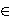
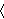 (1 - √709)/6 ,
(1 + √709)/6
(1 - √709)/6 ,
(1 + √709)/6
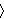 .
Presjek tog rješenja s uvjetom definiranosti
(lako je vidjeti da je 4 < (1 + √709)/6)
konačno je rješenje:
x
.
Presjek tog rješenja s uvjetom definiranosti
(lako je vidjeti da je 4 < (1 + √709)/6)
konačno je rješenje:
x 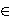 [ 4, (1 + √709)/6
[ 4, (1 + √709)/6
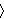 .
.
Jednadžbe
- √(x+2)(x+3) - √(x+3)(x+4) = 0
- 3√9 - √(x-1) + 3√7 + √(x+1) = 4
- 2 √5 4√(x+1) + 4 - √2 4√(x+1) - 1 = √20 4√(x+1) + 5
- 6 3√x-3 + 3√x-2 = 5 6√(x-2)(x-3)
- 5√(x-2)(x-32) - 5√(x-1)(x-33) = 1
- √x - 2√(x-1) + √x + 3 - 4√(x-1) = 1
- √(log√x (x2(1+x2)) + 4) = logx(1+x2)
Nejednadžbe
- √x2-5x+6 < √x2-7x+10
- 3√1-x2 ≥ 3√6+x-x2
- √x2-3x-10 < 8 - x
- √x2-16 / √x-3 + √x-3 > 5 / √x-3
- √x + 2√(x-1) + √x - 2√(x-1) > 3/2
- √2(5x + 27) - √5x - 7 ≥ √5x + 7
- √(3 - 9√2-x + 2 . 3√2-x ) + 2 . 3√2-x > 4
