
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://www.math.hr/~mathe/ |
Petar Damjan Ohmučević i računanje volumena broda
Marija Mlinarević
1. Uvod
2. Kako se računao volumen broda do Ohmučevićeva vremena?
3. Koji postupak računanja volumena predlaže Ohmučević?
4. Pojam integrala
5. Kako danas računamo volumen broda?
Literatura
Hrvatska je tijekom svih stoljeća bila pomorska zemlja. Hrvatski pomorci stalno su se bavili pomorskim problemima, koji su na razne načine bili povezani s matematikom. U 17. stoljeću ta se povezanost može uočiti u dva vida: u određivanju volumena broda i u pomorskoj nastavi. Problem određivanja volumena broda postojao je od davnina, no u 17. stoljeću dobiva sve naglašeniji teoretski značaj, a pomorska obuka, koja se obavljala prenošenjem pomorskih znanja, postaje sve organiziranija. Dubrovčani su gradili dobre brodove i sigurno im je bilo važno odrediti njihov volumen. Da je bilo tako, pokazuje rad pomorskog stručnjaka Petra Damjana Ohmučevića u Dubrovniku sredinom 17. stoljeća.
Petar Damjan Ohmučević rodio se u uglednoj pomorskoj i brodovlasničkoj obitelji u Slanom kraj Dubrovnika. Tijekom više stoljeća pripadnici ove obitelji bili su vrsni pomorci, a služili su i izvan Dubrovnika, posebno u pomorskoj službi Španjolske. Godina rođenja i smrti tog dubrovačkog pomorskog pisca i matematičara nije poznata, ali se zna da je u službu Dubrovačke Republike stupio 1644. godine kao učitelj aritmetike. Pripadao je uglednom dubrovačkom bratstvu Antunina. U Dubrovniku je službovao oko 12 godina, a zatim je 1656. godine napustio Dubrovnik i otišao u Napulj.
Napisao je na talijanskom dva djela iz područja matematike, koja su ostala u rukopisu, a nalaze se pohranjena u Toledu u Španjolskoj. To su: Succinto discorso di geometria pratica (Kratak razgovor o praktičnoj geometriji) i Trattato generale dei numeri rotti e del mododi estrarre la radice quadrata e la radice cuba, con vera regola di archiare e misurare le navi (Opća rasprava o razlomcima i o načinu vađenja drugog i trećeg korijena s ispravnim pravilom za proračunavanje i mjerenje brodova). Budući da je Petar Damjan Ohmučević bio više godina nastavnik matematike u Dubrovniku, gotovo je sigurno da je ta djela pisao kao neku vrstu školskih priručnika. Prvo od njih odnosilo se na praktičnu geometriju, a drugo je imalo za sadržaj razlomke i vađenje drugog i trećeg korijena. Drugo djelo sadržavalo je i pomorsku problematiku koja je bila jako povezana s matematikom. Tu je izloženo jedno pravilo za izračunavanje volumena broda. Izvadak o tom pravilu sačuvao se u dubrovačkom Historijskom arhivu pod naslovom Del modo di mesurare, o arciare le navi di qualsivoglia genere e forma, e riduli con detto archiamento alla giusta portata di tanti carra di tomola trentasei l'uno (O načinu mjerenja ili proračunavanja volumena broda bilo koje vrste i oblika, i o određivanju točnog iznosa u kolima od po 36 tomola na temelju ovog proračunavanja volumena). Taj problem nije se slučajno našao u sklopu tog aritmetičkog djela budući da se često dovodio u vezu s vađenjem trećeg korijena, osobito u nekim starijim postupcima koje Petar Damjan Ohmučević opisuje. To je djelo najvjerojatnije većim dijelom napisano za Ohmučevićeva boravka u Dubrovniku, gdje se bavio nautičkim problemima, a dovršio ga je u Napulju 1661. godne.
Određivanje volumena broda u brodogradnji od davnina je bio vrlo težak problem. Matematički ispravno nije ga nitko ni pokušavao riješiti budući da je brod omeđen brodskom oplatom koja je zakrivljena, a kod različitih tipova brodova i različitog oblika. Upravo zbog te kompliciranosti problema koristili su se mnogi aproksimativni postupci. Te su aproksimacije bile katkada bolje, a katkada lošije, ali često vrlo nepouzdane pa i pogrešne u svom temelju.
Upravo te stare postupke određivanja volumena broda Ohmučević opisuje na početku navedenog poglavlja. Tim postupcima on nije bio zadovoljan. U ranije doba, kada su oblici brodova bili vrlo slični, a linija i oblik brodova nisu se mnogo mijenjali, jedna je aproksimacija mogla zadovoljiti gotovo sve brodove koji su se gradili. U svojoj raspravi Ohmučević navodi dva tada postojeća načina izračunavanja volumena broda.
Prvi je postupak, kako on kaže, bio: "Pomnoži se najprije dužina sa širinom, a zatim taj umnožak s visinom. Od rezultata se odbije jedna trećina da se dobije stvarni volumen broda. Od toga opet pet posto radi neiskorištenih prostora na pramcu i krmi." Govoreći o tom postupku, Ohmučević kaže: "Tim se načinom služi Arsenal u Veneciji, cijeli Jadranski zaljev i Levant, kao i Mediteran do Barcelone." Ovim su se postupkom do tada služili i brodograditelji u Dubrovniku. Ohmučević nastavlja: "A budući da se stvarno taj način računanja volumena broda temelji na kubnom korijenu i na ostalim zapažanjima praktičara, mogli bismo reći da bi to bio pravi način za mjerenje volumena broda i savršeno ispravno pravilo kad bi poslovođe gradili brodove na starinski način; ali s obzirom da se s vremenom ne mijenjaju samo stari uzori u izgradnji nava i galeona, nego i sve ostale stvari i sve se više usavršavaju u ljepoti, skladu i brzini jedrenjaka, pravilo navedenog mjerenja postaje netočno i mnogo se udaljuje od pravilnog. Ne možemo taj nedostatak pripisivati navedenom pravilu ili onome koji ga je u ono vrijeme postavio, jer je onda bilo savršeno i njegovoga pronalazača možemo samo pohvaliti."
Drugi način sastojao se u tome da se najprije dužina i širina broda zbroje i taj zbroj pomnoži s visinom. Ohmučević napominje: "Dosta je zamisliti koliku vezu to ima s kubatorom." Nikakvu, jer se dobiva umnožak od samo dviju vrijednosti. On stoga kaže: "Drugi način mjerenja upotrebljavaju neki u Napuljskom Kraljevstvu. Za njih bez zamjerke moramo primijetiti da nijesu vješti ni u pomorskom znanju ni u umijeću mjerenja brodova; to mjerenje oni vrše na palme ili canne, bez osnove u nekom geometrijskom pravilu, osim ako nije napipano u zraku, jer ne vodi računa o činjenici da je volumen tijela proporcionalan koliko s dužinom i širinom, toliko i s visinom tijela."
Ovo je dobro mjesto da se upoznamo s mjernim jedinicama korištenim u 17. stoljeću. Petar Damjan Ohmučević služio se mjerama koje tada nisu bile posvuda jedinstvene. Kao mjeru za duljinu primjenjuje stopu, koja je u Veneciji iznosila 0.347735 m, a u Dubrovniku 0.3423 m. Uvodi i kubičnu stopu. Salma je bila mjera za volumen žita, a upotrebljavala se i za proračunavanje volumena broda. Kola ili kar (carro) bila je u mediteranskim zemljama mjera za volumen broda (za žitarice, vino itd.). Tomolo je bila mjera za volumen žitarica, a pedalj stara dužinska mjera primjenjivana kod gradnje brodova. Napuljski pedalj iznosio je 0.264 m, a dubrovački 0.256 m.
Iz kritičke primjedbe na dotadašnje metode računanja volumena broda, vidljivo je da je Ohmučević imao jasan stav o ispravnom načelu proračunavanja. Realno i s puno iskustva, gledajući na teoriju, on ispravno kaže: "U svakoj znanosti i umijeću traži se praksa za savršeno djelovanje u njoj. Iako imam malo znanja u geometriji kao i u mjerenju bilo koje vrste broda, lađa i galija, uz neprekidnu praksu kroz 13 godina, koju sam imao u svojoj domovini, uvjeren sam da znam savršeno naći prave račune imajući naročito naklonost i zadovoljstvo radeći i tražeći istinu." Kako se brodovi međusobno razlikuju po obliku, a oblik je pojedinog broda nemoguće obuhvatiti jednom formulom, Ohmučević predlaže da se brod podijeli okomito na spojnicu pramca i krme na nekoliko dijelova, najčešće na tri, ali po mogućnosti da se uzme i više podjela. Tada za svaki od tih dijelova Ohmučević uzima dužinu, širinu i visinu na početku i na kraju odsječka. Za svaku od tih dimenzija uzima aritmetičku sredinu i tako dobivene srednje duljine, širine i visine međusobno množi. Konačno još uzima i jednu korekciju zbog zaobljenosti tih dijelova. Nakon toga nalazi i zbroj svih dijelova broda koje je uzeo na početku. Ohmučević smatra da će uz veći broj podjela točnost rezultata biti veća. Ako njegov postupak usporedimo s ranijima, vidi se da je Ohmučevićev znatno bolji. On je ispravno kritizirao prijašnje i njihove nedostatke izbjegavao u svom postupku. Ohmučević ne želi da se njegov postupak temelji samo na empiriji, kao što su se temeljili drugi postupci, nego da se zasniva na jasnim geometrijskim temeljima. Najvrednija njegova misao sastoji se u tvrdnji da će volumen biti to točnije određen što se uzme više podjela.
Petar Damjan Ohmučević prikazao je svoj proračun volumena broda na brodu galijun (galeon) koji se u 16. i 17. stoljeću gradio u Dubrovniku jer je bio prikladan za oceansku plovidbu. Dubrovnik je već potkraj 15. stoljeća, a možda i prije, bio s Engleskom u pomorskoj trgovini.

Ohmučevićevi prijedlozi nisu puno zaostajali za radom nekih, kasnije svjetski poznatih, matematičara 17. stoljeća koji su se bavili vrlo sličnim problemom - određivanjem volumena bačve. U prvoj polovici 17. stoljeća mnogi su matematičari prihvatili nedjeljive dijelove geometrijskih objekata. Podržavao ih je i Johannes Kepler (1571.-1630.), koji je u djelu Nova stereometria doliorum vinariorum (Nova stereometrija vinskih bačava), objavljenome 1615. godine u Linzu, riješio težak problem određivanja volumena vinske bačve. Taj je problem uspio riješiti zahvaljujući tome što je bačvu promatrao kao da je sastavljena od nedjeljivih tankih listova, odnosno njezin je volumen shvatio kao zbroj tih nedjeljivih dijelova. Upravo to je do kraja razrađen Ohmučevićev prijedlog o što većem broju podjela. Kepler općenito govori o volumenima kao da su sastavljeni od infinitezimalnih elemenata iste dimenzije, a katkad ih naziva indivizibilima. Sličan stav zastupali su i Galileo Galilei (1564.-1642.) i njegov učenik i prijatelj Bonaventura Cavalieri (1598.-1647.), koji stavlja nedjeljive dijelove u temelj svojih matematičkih istraživanja. U knjizi Geometria indivisibilibus continorum (Geometrija o indivizibilima kontinuuma), objavljenoj 1635. godine, Cavalieri uvodi dosljedno izraz indivizibil, kojim označuje infinitezimalne elemente. Njegovim poučcima bavili su se mnogi matematičari u 17. stoljeću, a njihov rad preteča je infinitezimalnom računu.
Kratko smo se upoznali s idejama matematičara 17. stoljeća o računanju volumena.
Na istoj ideji zasniva se moderna definicija
Riemannovog
(određenog) integrala, koju ćemo sada izložiti. Za podskup skupa realnih brojeva
S 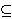
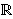 kažemo da je
ograničen ako postoje m, M
kažemo da je
ograničen ako postoje m, M 
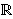 takvi da
je
takvi da
je 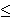 x
x 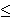 M,
M, S. Broj m zovemo
donjom međom, a M gornjom međom skupa S.
S. Broj m zovemo
donjom međom, a M gornjom međom skupa S.
Za broj m  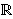 kažemo da je infimum skupa
S kažemo da je infimum skupa
S 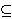 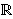 ako vrijedi: ako vrijedi:
|
Na analogan način definiramo supremum (sup S) kao najmanju gornju među skupa S. Jedno od osnovnih svojstava skupa realnih brojeva jest da svaki njegov ograničen podskup ima infimum i supremum (to je tzv. aksiom potpunosti).
Za funkciju f : [a,b] 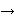
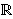 kažemo da je
ograničena ako je njezina slika
kažemo da je
ograničena ako je njezina slika 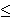 x
x 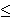 b}
b}
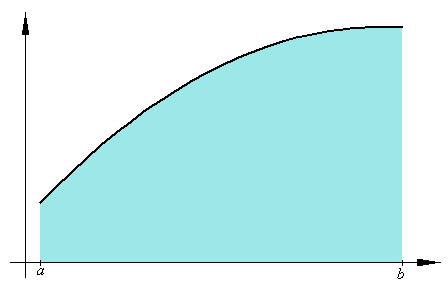
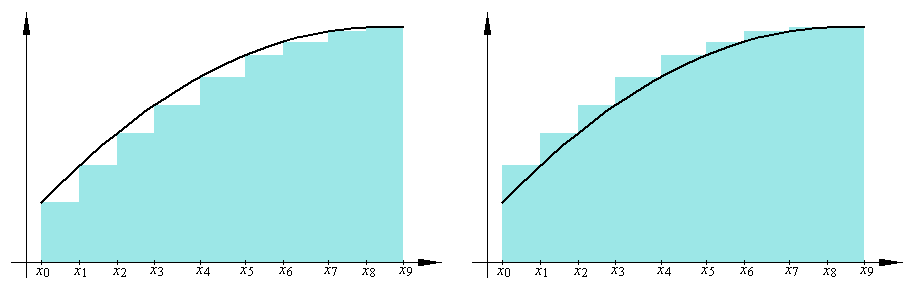
Podijelimo segment [a,b] točkama a = x0 < x1 < ... < xn-1 < xn = b na n dijelova, jednakih ili ne. Neka je mk infimum, a Mk supremum funkcije f na segmentu [xk-1, xk]. Promotrimo sljedeće sume:
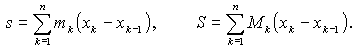
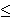 s
s 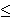 S
S 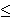 M(b - a),
gdje je m infimum, a M supremum funkcije f na [a,b].
M(b - a),
gdje je m infimum, a M supremum funkcije f na [a,b].
Neka je A skup svih donjih, a B skup svih gornjih Darbouxovih suma
funkcije f. One se dobivaju tako da se prirodni broj n i
točke xk uzimaju na sve moguće načine. Iz prethodne
nejednakosti vidimo da su A i B ograničeni skupovi pa imaju
supremum i infimum. Supremum skupa A nazivamo donjim Riemannovim
integralom, a infimum skupa B gornjim Riemannovim integralom
funkcije f. Pokazuje se da uvijek vrijedi
sup A 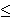 inf B.
inf B.
Za ograničenu funkciju f : [a,b] 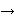 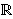 kažemo da je
integrabilna u Riemannovom smislu ako je njezin donji Riemannov integral jednak
gornjem Riemannovom integralu.
Tada taj broj zovemo Riemannovim ili određenim integralom
funkcije f na segmentu [a,b] i označavamo kažemo da je
integrabilna u Riemannovom smislu ako je njezin donji Riemannov integral jednak
gornjem Riemannovom integralu.
Tada taj broj zovemo Riemannovim ili određenim integralom
funkcije f na segmentu [a,b] i označavamo
|
Ako je f(x)  0
za svaki x
0
za svaki x  [a,b],
površina pseudotrapeza P(T) jednaka je određenom integralu funkcije f na
[a,b]. To je zapravo definicija pojma površine. U modernoj definiciji
ne spominju se infinitezimalne (beskonačno male) veličine, ali je možemo opravdati i
na taj način, bliži shvaćanjima 17. stoljeća. Zamislimo da je pseudotrapez podijeljen
prugama beskonačno male širine dx. Površinu jednog dijela nazivamo diferencijalom
površine i označavamo dP. Površinu svakog dijela možemo aproksimirati površinom
pravokutnika kojemu je jedna stranica dx, a druga f(x):
dP = f(x)dx. Ukupnu površinu dobit ćemo zbrajajući
(integrirajući) diferencijale površine:
[a,b],
površina pseudotrapeza P(T) jednaka je određenom integralu funkcije f na
[a,b]. To je zapravo definicija pojma površine. U modernoj definiciji
ne spominju se infinitezimalne (beskonačno male) veličine, ali je možemo opravdati i
na taj način, bliži shvaćanjima 17. stoljeća. Zamislimo da je pseudotrapez podijeljen
prugama beskonačno male širine dx. Površinu jednog dijela nazivamo diferencijalom
površine i označavamo dP. Površinu svakog dijela možemo aproksimirati površinom
pravokutnika kojemu je jedna stranica dx, a druga f(x):
dP = f(x)dx. Ukupnu površinu dobit ćemo zbrajajući
(integrirajući) diferencijale površine:
| P(T) = |
|
|
f(x) dx. |
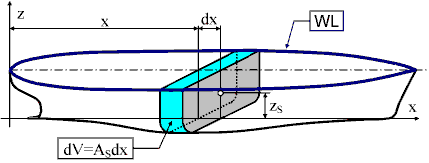
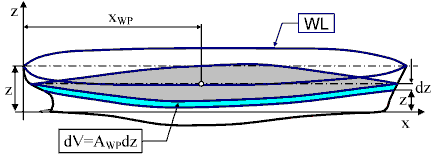
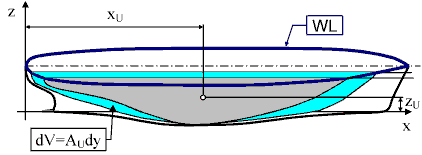
Metoda rebara najsličnija je Ohmučevićevom prijedlogu podjele broda poprečnim ravninama, okomitim na spojnicu pramca i krme. Diferencijalni volumen omeđen je dvama infinitezimalno udaljenim presjecima poprečnim ravninama. Pretpostavljamo da znamo odrediti površinu poprečnog presjeka AS(x) za svaku koordinatu x. Tada su diferencijalni volumeni slojeva jednaki dV = AS(x) dx. Ukupan volumen dobivamo zbrajajući te doprinose, odnosno integrirajući diferencijalne volumene po dužini broda:
| V = |
|
|
AS(x) dx, |
[D1] Ž. Dadić, Povijest ideja i metoda u matematici i fizici. Školska knjiga, Zagreb, 1992.
[D2] Ž. Dadić, Hrvati i egzaktne znanosti u osvit novovjekovlja. Školska knjiga, Zagreb, 1994.
[GR] I. Grubišić, Geometrija broda. Sveučilište u Zagrebu, 2001. http://www.fsb.hr/geometrija.broda/
[KU] S. Kurepa, Matematička analiza 1. Tehnička knjiga, Zagreb, 1975.
[MU] V. Muljević, Petar Damjan Ohmučević – nastavnik matematike u Dubrovniku u XVII. stoljeću. Hrvatski patentni glasnik 5-6 (1994), 575-578.
[UN] Š. Ungar, Matematička analiza 3. Sveučilište u Zagrebu, 2004.
1. Uvod
2. Kako se računao volumen broda do Ohmučevićeva vremena?
3. Koji postupak računanja volumena predlaže Ohmučević?
4. Pojam integrala
5. Kako danas računamo volumen broda?
Literatura