Zadaci

1. Svaka točka ravnine obojena je crvenom ili plavom bojom, pri čemu postoji barem jedna crvena i barem jedna plava točka. Da li je moguće da svaka kružnica polumjera 1 sadrži točno:
   a) jednu plavu točku;
   b) dvije plave točke?
   
   
2. Neka je P unutrašnja točka trokuta ABC. Neka su A₁B₂, B₁C₂, C₁A₂ pravci kroz točku P, redom paralelni s AB, BC, CA, pri čemu točke A₁, A₂ leže na stranici BC, točke B₁, B₂ na CA i točke C₁, C₂ na AB. Dokaži da vrijedi P(A₁A₂B₁B₂C₁C₂)≥ ⅔P(ABC), gdje je P površina odgovarajućeg lika.
   
   
3. Promatrajmo trokut ABC kod kojeg su duljine stranica a, b, c prirodni brojevi takvi da je M(a,b,c)=1. Simetrala kuta ∠BAC siječe BC u točki D.
   a) Dokaži da ako je trokut DBA sličan trokutu ABC, tada je c potpun kvadrat.
   b) Za svaki potpun kvadrat c=n², n≥2, nađi trokut ABC koji je sličan odgovarajućem trokutu DBA.
   
   
4. Neka su m,n prirodni brojevi i neka su x_i,j∈[0,1] za i=1,2,…,m; j=1,2,…,n. Dokaži nejednakost
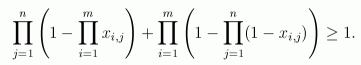