


14. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE
Omišalj, 4. - 7. svibnja 2005.
Zadaci za VII. razred
- Odredi troznamenkasti broj
abc
tako da je dvoznamenkasti broj
ac
jednak 12% broja
abc.
- Sok od naranče određene koncentracije dobije se
razrijeđivanjem narančinog sirupa vodom. U jednoj boci
nalazi se sok koncentracije 20%, a u drugoj koncentracije 50%.
Kad bismo 1/6 soka iz prve boce prelili u drugu bocu,
sok u drugoj boci bio bi konventracije 42.5%.
Kad bismo soku iz prve boce dodali sav sok iz druge boce
i još 3 litre vode, dobili bismo sok koncentracije 22.5%.
Koliko je soka u kojoj boci?
- Koliko ima uređenih parova cijelih brojeva (m,n)
takvih da je
|m| + |n| < 2005 ?
- Konstruiraj trokut ABC ako je
va = 3.5 cm, b = 4 cm
i polumjer opisane kružnice r = 3 cm.
- Dan je šiljastokutan trokut ABC. Simetrala kuta
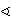 ABC
siječe krak
AC u točki D.
Okomica točkom D na simetralu BD siječe pravac AB u točki F.
Paralela točkom D s osnovicom AB siječe krak
BC u točki E,
a visinu iz vrha C na osnovicu
AB u točki M.
Dokaži da je
ABC
siječe krak
AC u točki D.
Okomica točkom D na simetralu BD siječe pravac AB u točki F.
Paralela točkom D s osnovicom AB siječe krak
BC u točki E,
a visinu iz vrha C na osnovicu
AB u točki M.
Dokaži da je |DM| = |FB| / 4 .
