



46. MEĐUNARODNA MATEMATIČKA OLIMPIJADA
Merida, Meksiko, 8. - 19. srpnja 2005.
Zadaci
- (Rumunjska)
Na stranicama jednakostraničnog trokuta ABC
nalazi se šest točaka: A1 i A2
na BC,
B1 i B2 na
CA te
C1 i C2 na
AB. Te
točke su vrhovi konveksnog šesterokuta
A1A2B1B2C1C2 čije
stranice imaju jednake duljine. Dokažite da se pravci
A1B2,
B1C2 i C1B2 sijeku u jednoj točki.
- (Nizozemska)
Neka je a1, a2, ...
niz cijelih brojeva koji ima beskonačno mnogo pozitivnih
i beskonačno mnogo negativnih članova. Poznato je da za svaki
prirodan broj n, brojevi
a1, a2, ... ,
an
daju n različitih ostataka
pri dijeljenju s n. Dokažite da se svaki cijeli broj
pojavljuje u ovom nizu točno jedanput.
- (Južna Koreja)
Neka su x, y i z pozitivni realni
brojevi takvi da je xyz
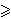 1.
Dokažite da je
1.
Dokažite da je
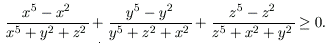
- (Poljska)
Niz a1, a2, ...
definiran je s
an = 2n + 3n + 6n - 1 (n = 1, 2, ... ).
Nađite sve prirodne brojeve koji su relativno prosti sa svakim članom ovog niza. - (Poljska)
Neka je ABCD konveksan četverkut čije stranice
BC i
AD
imaju jednake duljine i nisu
paralelne. Neka je E točka na stranici
BC,
različita od B i C te neka je F točka na stranici
AD,
različita od A i D, tako da je |BE| = |DF|.
Pravci AC i BD sijeku se u točki P, pravci BD i EF u
točki Q, a pravci EF i AC u točki R. Promotrimo trokute
PQR koje dobivamo za sve takve točke E i F. Dokažite da ovim
trokutima opisane kružnice imaju zajedničku
točku različitu od P.
- (Rumunjska)
Na matematičkom natjecanju bilo je zadano 6
zadataka. Pokazalo se da je svaki par zadataka riješilo
više od
2/5 ukupnog broja natjecatelja, ali nitko nije riješio svih 6 zadataka. Dokažite da postoje barem 2 natjecatelja takva da je svaki od njih riješio točno 5 zadataka.
