Hrvatski matematički elektronski časopis math.e
	http://web.math.hr/mathe/

11. DRŽAVNO NATJECANJE MLADIH MATEMATIČARA REPUBLIKE HRVATSKE

Zadar, 2. - 5. svibnja 2002.

Zadaci za IV. razred

1. Izračunajte beskonačni zbroj

   s = 1 + 4x + 9x² + ... + n²x^{n -1} + ... ,

   gdje je |x| < 1.

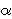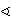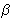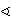2. Vrhovi kocke u prostornom koordinatnom sustavu s ishodištem O su u točkama A(1,1,1), A'(-1,-1,-1), B(-1,1,1), B'(1,-1,-1), C(-1,-1,1), C'(1,1,-1), D(1,-1,1), D'(-1,1,-1). Točka O je središte kocki opisane sfere. Neka točka T nije na toj sferi i d = |OT|. Označimo s = ATA', = BTB', 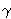= 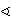CTC' i 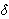= 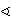DTD'. Dokažite da je

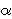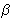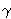   tg² + tg² + tg² + tg²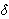 = 32d² / (d² - 3)²   .

3. Neka je f(x) = x²⁰⁰² - x²⁰⁰¹ + 1. Dokažite da su za svaki prirodan broj m brojevi m, f(m), f(f(m)), f(f(f(m))), ... , u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od 1.

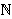4. Neka je (a_n), n , rastući niz prirodnih brojeva. Za član a_k tog niza kažemo da je dobar ako se može prikazati kao suma nekih drugih (ne nužno različitih) članova tog niza. Dokažite da su svi članovi tog niza, osim njih konačno mnogo, dobri.