
 |
Hrvatski matematički elektronski časopis math.e | |
| Broj 8 | ||
| http://web.math.hr/mathe/ |
Tvrdnja: Wangove pločice računaju Fibonaccijeve brojeve, od 3 nadalje.
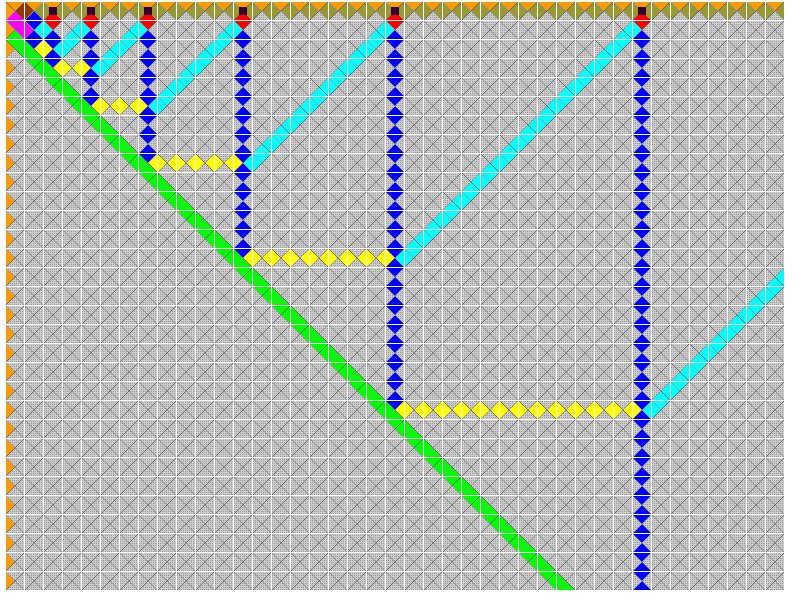
"Dokaz": Kao što se vidi na slici, prvih 6 crnih točaka nalazi se u redom 3., 5., 8., 13., 21. i 34. stupcu. Također, vidi se da su iznad zelene linije koja ide koso dolje uvijek ili žuti horizontalni i svijetloplavi kosi niz kvadratića, ili plavi vertikalni niz.
Jasno je da plavi niz mora ići do vrha, jer nemamo niti jednu pločicu s narančastim dolje, a plavi vertikalni niz može završiti samo crvenom (a ona odmah završava s narančastom) ili direktno s narančastom.
Također, kosi svijetloplavi niz kvadratića mora doći do vrha (jedina terminalna pločica za taj niz prema gore jest ona lijevo svijetloplava, desno prazna, gore crvena i dolje plava, pa je to terminalna plocica i za plavi niz). Dakle, kada svijetloplavi dođe do vrha imamo vertikalni plavi niz. Tu također imamo i izlazni podatak.
Sjecište vertikalnog plavog i horizontalnog žutog niza je nužno početak svijetloplaovog niza (samo takvu pločicu za sjecište imamo). Ako je to sjecište bilo u n-tom retku, onda će sjecište svijetloplavog i sljedećeg plavog niza biti n-1 mjesto dalje (jer se do drugog retka kosi svijetloplavi niz penje kroz n-1 korak).
Sjecište vertikalnog plavog i padajućeg zelenog niza je početak žutog niza kvadratića, pa žuti kvadratići "pamte" red u kojemu je iz zelenog niza počeo prošli plavi niz. Žuti nizovi počinju uvijek u k-tom stupcu i (k+1)-vom retku.
Ako su dva uzastopna izlazna podatka bili na mjestima fa i fa + 1, tada u fa-tom stupcu počinje žuti niz u fa + 1-vom retku. Taj žuti niz ide do fa + 1-tog retka, gdje završava žuti i počinje svijetloplavi niz. Kako znamo iz ranijeg računa, svijetloplavi niz dođe do drugog reda u točno (fa + 1) - 1 = fa narednih koraka i tamo "postavi" izlazni podatak. No, to znači da se fa + 2-i podatak nalazi u fa + fa + 1-om stupcu (u međuvremenu nije moglo biti izlaznih podataka, jer svakom izlaznom podatku pripada vertikalni plavi niz i kosi svijetloplavi, a takvih nismo imali putem). Dakle, vrijedi fa + 2 = fa + 1 + fa. No, kako se iz slike vidi, f1 = 3 i f2 = 5, pa je fa podniz Fibonaccijevih brojeva.
Siniša Miličić, apsolvent, PMF-Matematički odjel, Zagreb