Rješenje 1. zadatka u 3. broju
a)
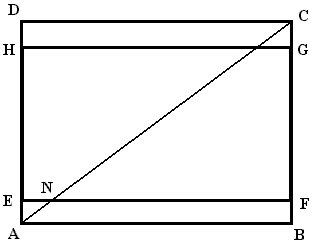
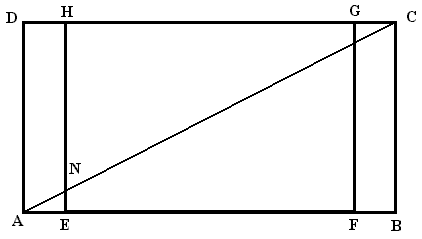
Prikažimo klasični ekran kao pravokutnik ABCD,
(|AB| = a,
|BC| = 3/4 a),
a sliku na ekranu kao pravokutnik EFGH,
(|EF| = a,
|FG| = 9/16 a).
Kako su obje crne pruge jednake, zaključujemo da je
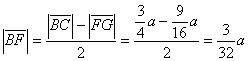
Neka dijagonala AC
siječe EF
u točki N. Očito je da su trokuti NFC i ABC slični (jer su im svi kutovi jednaki) pa vrijedi
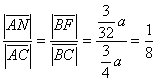
Dakle, neiskorištenim ostaje
2 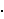 1/8 = 1/4
dijagonale, što je 25%.
1/8 = 1/4
dijagonale, što je 25%.
b)
Prikažimo widescreen ekran kao pravokutnik
ABCD, (|AB| = a,
|BC| = 9/16 a),
a sliku na ekranu kao pravokutnik EFGH,
(|EF| =
9/16 a 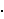 4/3 = 3/4 a,
|FG| = 9/16 a).
Kako su obje crne pruge jednake, zaključujemo da je
4/3 = 3/4 a,
|FG| = 9/16 a).
Kako su obje crne pruge jednake, zaključujemo da je
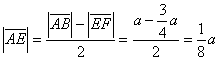
Neka dijagonala AC
siječe EH
u točki N. Očito je da su trokuti AEN i ABC slični (jer su im svi kutovi jednaki) pa vrijedi
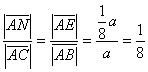
Dakle, neiskorištenim ostaje
2 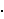 1/8 = 1/4
dijagonale, što je 25%.
1/8 = 1/4
dijagonale, što je 25%.
Slaven Kožić, student 1. godine, PMF-Matematički odjel, Zagreb


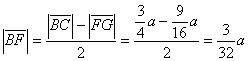
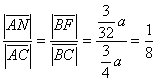
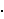 1/8 = 1/4
dijagonale, što je 25%.
1/8 = 1/4
dijagonale, što je 25%.

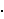 4/3 = 3/4 a,
|FG| = 9/16 a).
Kako su obje crne pruge jednake, zaključujemo da je
4/3 = 3/4 a,
|FG| = 9/16 a).
Kako su obje crne pruge jednake, zaključujemo da je
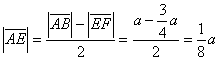
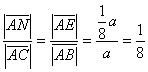
 1/8 = 1/4
dijagonale, što je 25%.
1/8 = 1/4
dijagonale, što je 25%.
