
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
x2 - 8x + 15 ≥ 0
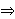 x
x 
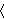
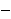
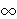 , 3]
, 3]
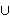 [5, +
[5, +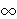
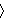 ,
,
x2 + 2x - 15 ≥ 0
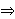 x
x 
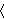
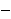
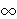 , -5]
, -5]
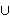 [3, +
[3, +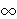
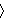 ,
,
4x2 - 18x + 18 ≥ 0
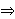 x
x 
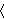
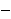
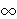 , 3/2]
, 3/2]
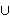 [3, +
[3, +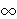
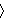 .
.
x 
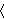
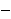
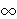 , -5]
, -5]
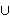 {3}
{3}
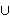 [5, +
[5, +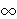
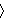 .
.
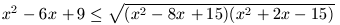 (*)
(*)
6x3 - 70x2 + 258x - 306 ≥ 0. (**)
Riješimo kubnu nejednadžbu (**). Dobivamo realna nulišta x1 = 3 i x2 = 17/3. Skiciramo graf te kubne funkcije i vidimo da je ona veća od nule za x
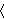 17/3,
+
17/3,
+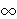
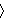 .
Dakle, rješenje kubne nejednadžbe, a ujedno i rješenje polaznog
zadatka, jest
.
Dakle, rješenje kubne nejednadžbe, a ujedno i rješenje polaznog
zadatka, jest
x  {3}
{3} 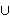 [17/3,
+
[17/3,
+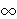
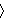 .
.
Marko Horvat, 4. razred, V. gimnazija, Zagreb