
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://web.math.hr/mathe/ |
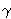 i
dužine A2B2 (točka C1)
ima koordinate (f,0), a tada točka C malog trokuta
ima koordinate (f, 1/2).
i
dužine A2B2 (točka C1)
ima koordinate (f,0), a tada točka C malog trokuta
ima koordinate (f, 1/2).
Preostale dvije točke B1 i A1 dobiju se kao rješenja sustava dvije jednadžbe s dvije nepoznanice, pretpostavivši d(M, B1) = 1, d(B1, A2) = f, te analogno za drugu točku A1. Dobivaju se rješenja:
A1 = ((f + 2g)/(1 + g2), 3/2 - 1/(1+g2)), B1 = ((f3 - f)/(1 + f2), 2f2/(1 + f2)).
Zatim se nađu jednadžbe pravaca kroz A2B1 i B2A1, te se nađe njihov presjek kako bi se dobile koordinate točke C2:C2 = ((f2 - 1)g/(fg - 1), 2fg/(fg - 1)).
Sada je moguće preko formule za površinu trokuta sa zadanim koordinatama vrhova izračunati površinu većeg trokuta. Dobije se da je površina trokuta A2B2C2 jednakaKoordinate od B i A moguće je dobiti kao polovišta dužina MB1 i MA1 jer tražene točke leže u središtima kružnica, dok poznate točke kojima znamo koordinate leže na presjeku promjera i kružnice, dakle na istom pravcu.
Tada istom formulom izrazimo površinu manjeg trokuta.
Dobivamo da je površina trokuta ABC jednaka
2(1 + f2)(1 + g2)/(fg - 1).