
Hrvatski matematički elektronski časopis math.e

|
Hrvatski matematički elektronski časopis math.e |
| http://www.math.hr/~mathe/ |
Matrične transformacije ravnine
Tvrtko Bedeković, Borko Jandras, Darko Žubrinić
Svakoj točki ravnine s koordinatama (x,y) pridružujemo točku druge ravnine s koordinatama (x',y'), koje računamo na sljedeći način:
x' = a x + b y
y' = c x + d y.
Koeficijenti a, b, c i d su unaprijed zadani realni brojevi. Odabiru se po volji i grupiramo ih u matricu A:
| A = |
|
Gornju transformaciju možemo kraće prikazati kao preslikavanje (linearni operator) A : R2 --> R2 opisano s:
v' = Av,
gdje je v = (x,y)T i v' = (x',y')T (T je transponiranje, tako da su v i v' vektori stupci).
Komponente vektora Ai i Aj (u kanonskoj bazi) su prema tome upravo vektori stupci matrice A, pa možemo uvjetno pisati da je A = [Ai,Aj].
Matrične transformacije ćemo ilustrirati tako da uzmemo neki lik u lijevom prozorčiću s koordinatnim sustavom (x,y) i pogledamo u što se on preslikava u desnom prozorčiću s koordinatnim sustavom (x',y').
Diskusiju koja slijedi možete testirati, a i sami eksperimentirati, pomoću dva efektna programa za vizualizaciju matričnih transformacija koje su izradili prvi i drugi autor ovog članka.
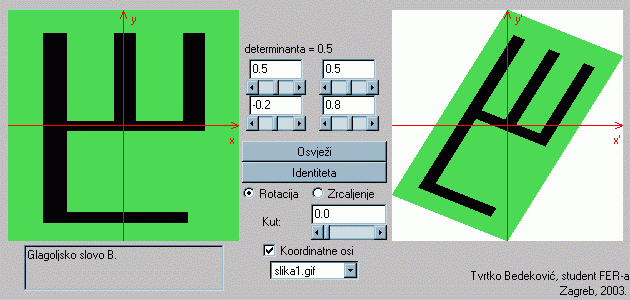
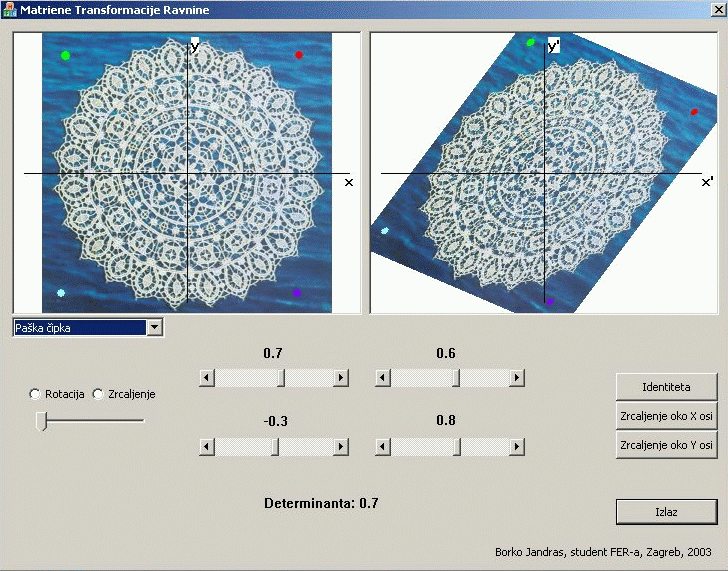
Primijetite da paralelogram P u lijevom prozoru uvijek prelazi u paralelogram P' u desnom.
S obzirom na regularnost matrice A imamo ove dvije mogućnosti.
| A = |
|
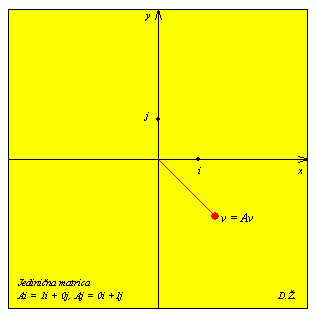
je x' = ax + by = x + y, y' = cx + dy = 2(x + y) = 2x'. Cijela ravnina se preslikava u pravac y' = 2x' i to je slika matrice A. Dimenzija slike jednaka je upravo rangu matrice, tj. ovdje je r(A) = 1. Nul-potprostor (ili jezgra) matrice A definira se kao skup rješenja jednadžbe Av = 0. Taj skup je za ovu matricu pravac y = -x :
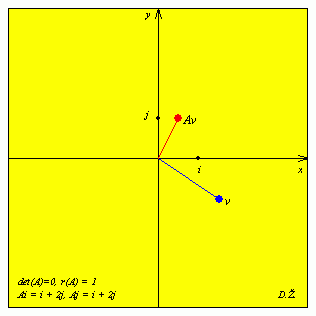
Koordinatni sustav x', y' se u gornjem appletu podudara s koordinatnim sustavom x, y. Vektor v zadaje se povlačenjem miša s pritisnutom lijevom tipkom. Nakon toga se za svaki vektor v skoro istoga trenutka izračunava vrijednost vektora Av.
| A = |
|
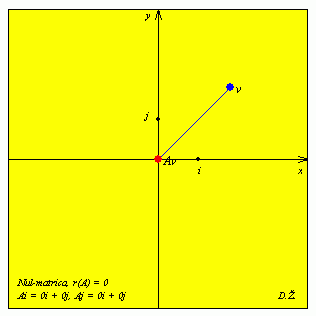
Nul-potprostor matrice A = 0 je cijela ravnina, tj. N(A) = R2, a slika od A je nul-potprostor, tj. nul-vektor.
Primijetite da će slučajnim odabirom svojih četiriju koeficijenata matrica A skoro sigurno biti regularna (tj. skoro sigurno će det A biti različita od nule). Točnije, može se pokazati da je vjerojatnost da slučajnim odabirom četiriju matričnih koeficijenata dobivena matrica A bude regularna (tj. det A nije nula) jednaka jedan.
Pogledajmo neke specijalne tipove matričnih transformacija ravnine.
| A = |
|
| A = |
|
| I = |
|
| A = |
|
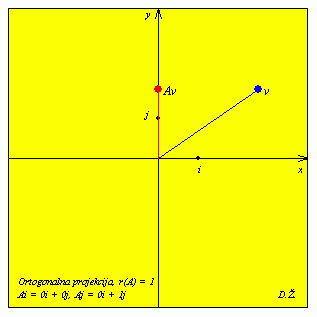
Nul-potprostor matrice A je os x, a slika je os y.
| A = |
|
| A = |
|
| A = |
|
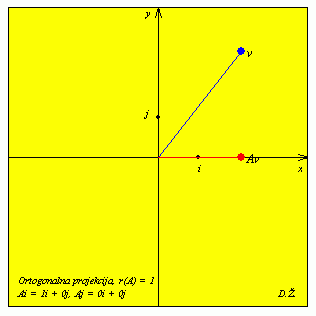
Nul-potprostor matrice A je os y, a slika je os x.
| A = |
|
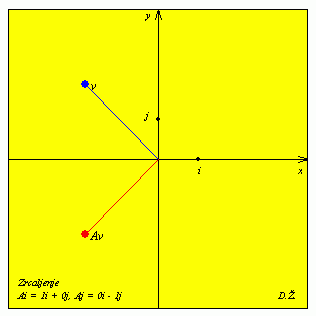
| A = |
|
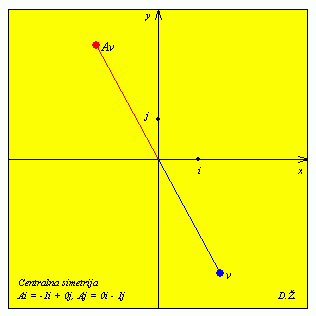
| A = |
|
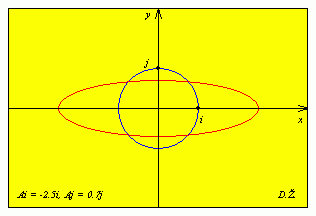
Može se pokazati da svaka regularna matrica preslikava kružnicu u elipsu, samo što osi elipse neće uvijek biti paralelne s koordinatnim osima.
| A = |
|
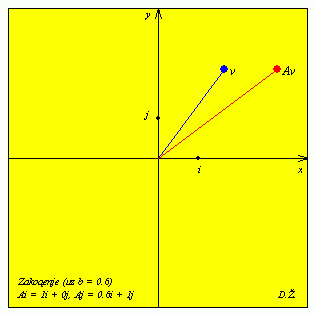
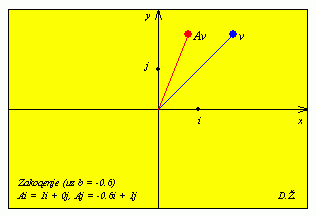
| A = |
|
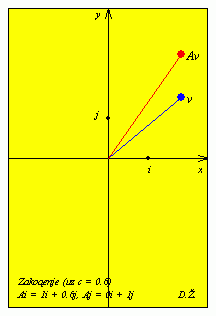
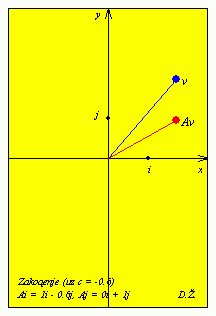
| A = |
|
Rotacija ravnine za 180 stupnjeva oko ishodišta isto je što i centralna simetrija ravnine s obzirom na ishodište.
| A = |
|
det A = ad - bc = -(cos 2s)2 - (sin 2s)2 = -1.
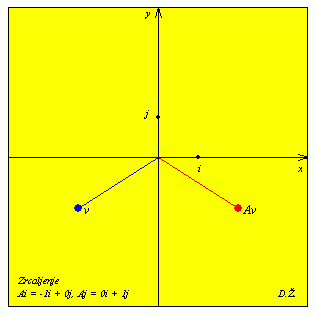
U programima za vizualizaciju unosi se samo kut s, nakon čega se obavlja zrcaljenje s obzirom na pravac y = (tg s) x.
| A = |
|
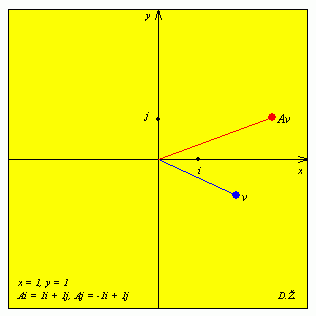
tj. A = xI + yJ, gdje je J matrična imaginarna jedinica, J2 = -I. Time smo dobili pridruživanje
x + iy --> xI + yJ
iz skupa kompleksnih brojeva C u skup matrica reda dva, M2,2. Jasno je da zbroju dvaju kompleksnih brojeva odgovara zbroj pripadnih matrica. Zanimljivo je da i umnošku dvaju kompleksnih brojeva odgovara umnožak pripadnih matrica. Naime, za kompleksne brojeve vrijedi:(x + yi)(u + vi) = (xu - yv) + (xv + yu)i,
kao i za pripadne matrice:(xI + yJ)(uI + vJ) = (xu - yv)I + (xv + yu)J,
gdje su x, y, u, v zadani realni brojevi, a i je imaginarna jedinica, i2 = -1.
P' =
|(ai + cj) x (bi
+ dj)| =
= |(ad - bc)k| =
|ad - bc| =
= |det A|.
| A = |
|
P' = |det A| P.
Ta činjenica je specijalan slučaj formule za zamjenu varijabli u dvostrukom integralu, koja uključuje pojam Jacobijana. Doista, Jacobijan J(f,g) funkcije iz R2 u R2 zadane komponentnim funkcijamax' = f(x,y)
y' = g(x,y)
za linearnu transformaciju f(x,y) = ax + by i g(x,y) = cx + dy jednak je točnoJ(f,g) = det A.
Podsjetimo se, Jacobijan se definira pomoću determinante matrice parcijalnih derivacija prvog reda:| J(f,g) = det |
|
| B = |
|
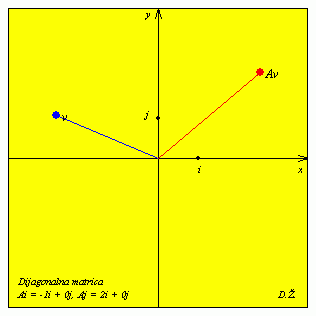
Za nju vrijedi Bi = -i i Bj = 2j. Prema tome, vlastite vrijednosti ove matrice su -1 i 2. Vlastiti potprostor za r = -1 je os x, a vlastiti potprostor za r = 2 je os y.
| A = |
|
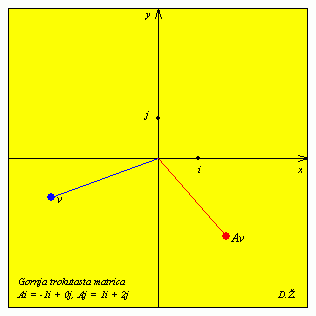
Vlastite vrijednosti su -1 i 2, a pripadni vlastiti vektori su i i i + 3j.
| A = |
|
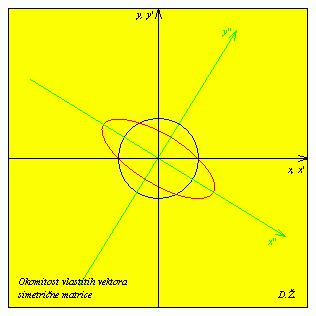
Kružnica u ravnini sa središtem u ishodištu simetričnom matricom preslikava se uvijek u elipsu. Glavne osi elipse su vlastiti potprostori simetrične matrice (ucrtani zelenom bojom). Omjer duljina poluosi elipse jednak je |r1/r2|, gdje su r1,2 vlastite vrijednosti matrice. Matrica A je slična matrici B = diag (r1, r2). U ovom primjeru je
a pripadni vlastiti vektori su
Vlastiti vektori su okomiti: (v1|v2) = 0. Matrica sličnosti je S = [w1, w2], gdje su vektori stupci w1 i w2 normirani vlastiti vektori od A (prema tome matrica T je ortogonalna, tj. S-1 = ST, vidi [Elezović]):
Drugim riječima, S-1AS = diag (r1, r2).
Njezina jednadžba u prirodnom (zelenom) koordinatnom sustavu glasi
Na lijevoj strani je kvadratna forma generirana simetričnom matricom A-2 = [{0, 1}, {0, 1}] * [{0, 1}, {0, 1}] = [{1, 1}, {1,2}]. Doista, uz pretpostavku da je simetrična matrica A regularna, iz v' = Av dobivamo
Vlastite vrijednosti matrice A-2 su ri-2, a vlastiti vektori isti kao kod A.
Pogledajte kao dodatnu ilustraciju
| T = |
|
tj. T-1AT = B. Matrica A nije simetrična. Primijetite da joj (za razliku od simetričnih matrica) vlastiti vektori koji pripadaju različitim vlastitim vrijednostima nisu međusobno okomiti.
Literatura