
| Leonardo i matematika |  |  |
|
Sadržaj: 1. UvodOvaj članak posvećen je matematici i matematičarima Leonardova vremena i interesu koje je genij Da Vinci pokazao za ovu disciplinu, koja je tijekom 15. i 16. stoljeća proživljavala važno razdoblje vlastite povijesti. Matematika prisutna u Leonardovim spisima, zvanim kodeksima, razlikuje dva perioda: period prije i period poslije susreta s Lucom Paciolijem. Što se tiče posljedne faze, u njoj se bavi istraživanjima vezanima za konstrukcije ravnalom i šestarom, kvadraturu kruga i upotrebu metode "pogrešne pozicije". Važno mjesto zaslužuju i poliedri realizirani na temelju Paciolijeva Božanskog omjera te poneka učenja vezana za popločavanja ravnine. Kroz Leonardov um pokušat ćemo pružiti drukčiju perspektivu, pozivajući vas da istražujete genijev način razmišljanja i njegovu jedinstvenu koncepciju znanja kroz trud asimilacije, preko jakih teorijskih sinteza i inventivnih eksperimenata te kroz zakone koji vladaju između ljudi i prirode. Ovakav pristup omogućuje drukčiju sliku, onu koja rješava misterij u koji je Leonardov mit često bio prekiven plaštom: um tvrdoglavo pokušava odgonetnuti racionalne procese koji pokreću fenomene fizičkog svijeta kao i tijek misli, vođen željom postizanja idealne imitacije prirode u crtežima i slikama. Neki smatraju da Leonardo nije imao ispravnu metodologiju u pristupu znanosti. No, imajmo na umu da je umro 45 godina prije rođenja Galilea Galileija te da je njegov svjež pristup obogatio kulturu i umjetnost svojega vremena. 2. Kratko o LeonarduLeonardo da Vinci (15. travnja 1452. - 2. svibnja 1519.) bio je talijanski slikar, arhitekt, izumitelj, glazbenik, kipar, pripovjedač, matematičar i inženjer. Ukratko - najveći genij renesanse, čovjek koji utjelovljuje renesansni ideal svestrana čovjeka, višestruko nadarena čovjeka neutažive znatiželje i žudnje za novim spoznajama. Samo jednostavno nabrajanje njegovih neumjetničkih interesa graniči s neshvatljivim: anatomija, botanika, kartografija, geologija, matematika, aeronautika, optika, mehanika, astronomija, hidraulika, akustika, niskogradnja, tehnika proizvodnje oružja, planiranje gradova... Njegova djela Posljednja večera (1495. - 1497.) i Mona Lisa (1503. - 1506.) spadaju među najpopularnije i najutjecajnije slike renesanse, dok njegovi spisi odražavaju duh znanstvenog istraživanja i mehaničke inventivnosti koja je bila stoljećima ispred svojega vremena. Umjetnik po dispoziciji, otkrio je da su mu oči bile glavni put do znanja; za Leonarda vid je bio čovjekov najviši organ čula zato jer vid sam pretvara činjenice u iskustva odmah, korektno i sa sigurnošću. To znači da svaki fenomen koji je promatran postaje objekt znanja. Saper vedere (znati kako vidjeti) postaje glavna tema njegovih proučavanja čovjekovih djela i kreacija prirode. Njegova kreativnost sezala je u svako područje u kojem se koristilo grafičko predstavljanje: bio je slikar, kipar, arhitekt i inženjer. Ali on je išao i iznad svega toga. Njegov veličanstven intelekt, neuobičajena snaga opservacije te majstorstvo umjetnosti crtanja vodili su ga u promatranje same prirode, koju je proučavao s metodičnošću i ubacujući logiku - u čemu su njegova umjetnost i znanost bile jednako zastupljene. Leonardov učinak je sažetak tog izvanrednog perioda ljudske povijesti poznatog kao talijanska renesansa, perioda velikih kulturnih prednosti i velikih projekata. Leonardova djela odraz su ljudi toga doba, onoga što su osjećali i činili, strojeva koje su gradili kako bi mogli graditi crkve, palače, dvorce; strojeve za vođenje rata, za rad, za proizvodnju i trgovinu svih onih roba čija je dostupnost bila od vrlo velike važnosti za vladare i njihove dvorove. No, još važnije, Leonardovi izumi svjedoče o tome tko i što je on bio - čovjek koji je bio oblikovan najomiljenijim i najstimulativnijim gradom toga doba, Firencom, potican na osnovi svog vlastitog uzorka istraživanja i skiciranja ideja i planova te koncentriran na više različitih sektora, rangiranih od hidraulike do mehanike, letenja, anatomije i optike... Trebamo samo pogledati neke od najinteresantnijih ideja sadržanih u više od 5000 stranica Leonardovih zapisa kako bismo shvatili veličinu njegovih misli. Unatoč činjenici da je bio bez formalnog obrazovanja, Leonardo je tijekom godina sakupio zavidnu biblioteku koja je obuhvaćala tekstove o filozofiji prirode, literarna djela te ona posvećena tehnici i umjetnosti. S autorima ovih tekstova Leonardo se aktivno upuštao u polemičke dijaloge, podvrgavajući čak i već priznate doktrine strogo racionalnom zaključivanju i iskustvenim dokazima. Broj i raznovrsnost knjiga u njegovoj biblioteci odražavaju znatiželju njegova uma koji se okušao u svim mogućim smjerovima istraživanja. Upotpunjen knjigama, Leonardov radni stol bio je mjesto gdje je probleme kojima se bavio zapisivao riječima, upotpunjenima skicama i crtežima, te eksperimentima provedenima ručno ili uz pomoć sofisticiranih instrumenata. Leonardo je sva svoja istraživanja zapisivao na listove papira, takozvane kodekse. Riječ je o 5000 stranica karakterističnog Leonardova rukopisa, pisanog zrcalno i zdesna ulijevo, na koje je zapisivao sve čime se bavio. Često su se na istom listu papira tako našli matematički proračuni, tehnički izumi, ali i umjetničke skice i studije. Poslije smrti njegova odana učenika Francesca Melzija (1493. - 1570.), kipar Pompeo Leoni (1533. - 1608.) taj je materijal grupirao tematski, izrezujući i spajajući pojedine dijelove srodnog sadržaja. Tako preuređeni, Leonardovi najvažniji znanstveni i inovatorski rukopisi danas su dostupni podijeljeni u deset svezaka:
S matematičkog gledišta, najzanimljiviji kodeksi su Atlanticus, Arundel, Forster, kodeksi Francuskog instituta i Madridski kodeksi. Kodeks Atlanticus izložen je u zagrebačkom Muzeju za umjetnost i obrt od 6.12.2006. do 25.2.2007. Leonardo je dospio u 21. stoljeće zahvaljujući svojoj modernosti, svojoj hrabrosti da se uputi na nesigurna područja, pogotovo na području prirodnih znanosti, zahvaljujući neustrašivom pogledu u bućnost i neprestanom trudu da uvijek bude korak ispred svoga doba. 3. Matematika i matematičari Leonardova dobaU ovom članku prije svega nas zanima "matematička strana" Leonardova genija. Želimo otkriti što je Leonardo znao o matematici i kakav je bio matematičar. Kako bi slika bila potpuna, najprije ćemo upoznati najvažnije matematičare njegova doba i reći nekoliko riječi o matematičkim problemima koji su zaokupljali njihove misli. Slično kao danas, i u doba talijanske renesanse matematičari su se bavili problemima algebre, aritmetike i geometrije. Algebra je u Leonardovo vrijeme smatrana uzvišenom, štoviše, teškom matematikom, a algebarski problemi kojima su se bavili tadašnji matematičari vezani su za rješavanje jednadžba trećeg i četvrtog stupnja. Raspravama i napretku teorije jednadžba i algebre najviše su pridonijeli sljedeći Leonardovi suvremenici:
Algebarska notacija koja se upotrebljavala u drugoj polovici 15. stoljeća dosta se razlikuje od današnje. Zanimljivo je istaknuti da su osnovni algebarski simboli kojima se danas uobičajeno koristimo stvoreni tek nekoliko desetljeća nakon Leonardove smrti, zahvaljujući Françoisu Vièteu (1540. - 1603.) i Renéu Descartesu (1596. - 1650.). Način matematičkog zapisivanja u 15. je stoljeću prolazio transformaciju od verbalne algebre, u kojoj su algebarski izrazi bili izraženi pomoću riječi, do sinkopirane algebre, u kojoj su se pojedini termini, npr. pojedine komponente jednadžbe, izražavali pomoću kratica. Čak je i napredni matematičar Girolamo Cardano još uvijek upotrebljavao opisni, a ne simbolički zapis: što bismo danas pisali kao U geometriji se u Leonardovo vrijeme proučavala geometrija ravnine i prostora te tada novootkrivena perspektiva. Analitička geometrija, unatoč pionirskim pokušajima Nicole d'Oresme, u to se doba još nije razvila i čekala je kreativnost Descartesa i Pierra de Fermata. Dvije za to vrijeme temeljne knjige u kojima možemo pronaći geometrijska istraživanja su starogrčki Euklidovi Elementi te Ottica (Optika), iznimno važna zbog svoje bitne povezanosti s perspektivom. Aritmetika koja se proučavala u Leonardovo vrijeme bila je vrlo elementarna, o čemu svjedoči i podatak da je prva tiskana matematička knjiga L'arte dell'abaco objavljena tek nešto prije Leonardova doba, 1478. u Trevisu u Italiji. 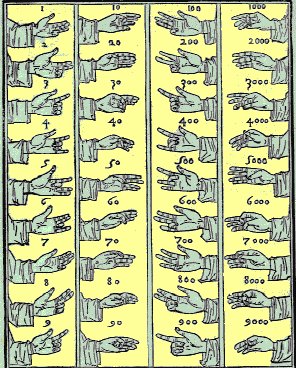
Knjiga, čiji je autor ostao nepoznat, bavi se evolucijom matematičkog znanja na zapadu. U njoj se upotrebljavaju arapski brojevi i proučavaju četiri osnovne aritmetičke operacije, što je potkrijepljeno brojnim primjerima i različitim tehnikama zapisa. U knjizi se pojavljuju i razlomci, no ne i decimalni brojevi, koji će svjetlo dana u matematici ugledati tek stotinjak godina kasnije. L'arte dell'abaco donosi i brojne definicije osnovnih matematičkih pojmova i operacija. U donjoj tablici nalazi se pregled svih autorovih saznanja o računskim operacijama.
Mnogo je matematičara 15. i 16. stoljeća koji su utjecali na Leonardov rad, a s nekima od njih imao je prilike i komunicirati. Pouzdano se zna da je kontaktirao s Pietrom Montijem, Giacomom Andreom da Ferrarom, dvojicom braće medicinara Marliani, te s Benedettom Aritmeticom dell'Abbacom. No, od svih je matematičara najveći utjecaj na Leonardov rad ipak imao Luca Pacioli (1445. - 1517.), putujući učitelj matematike koji je 1497. godine prihvatio poziv Ludovica Sforze da dođe raditi u Milano. Tamo je, među ostalima, matematici poučavao i Leonarda. Period boravka u Milanu bogat je matematičkim postignućima našega genija. O njima, kao i o presudnom utjecaju Luce Paciolija na Leonardovo poimanje matematike, više ćemo reći u idućim poglavljima. 4. Leonardova matematika prije susreta s PaciolijemS obzirom na njegovu matematiku, u Leonardovu životu odvajamo dva razdoblja - prije i poslije susreta s Lucom Paciolijem. Vidjet ćemo i zašto. Razlomci i aritmetikaNa temelju Leonardovih bilješki vidimo da nije znao baratati s razlomcima. U kodeksu Atlanticus Leonardo piše ovako:
U svojem se radu koristio mješovitim brojevima, koje je znao pretvoriti u obične razlomke, no nije ih znao zbrojiti. Npr. zapisao je sljedeće:
Rezultat je očito kriv i trebao bi biti jednak 45/12, što je jednako 15/4. Iz svega ovoga zaključujemo da Leonardo nije prepoznao broj 12 kao nazivnik, te je čudno kako je uopće dobio broj 78. Još jedan primjer je Leonardovo skraćivanje razlomka 270/360, što je danas vještina koja se očekuje od osnovnoškolaca. Leonardo je, doduše, dobio ispravan rezultat, 3/4, no više zbog svoje intuicije i analogije nego zbog svog znanja matematike. Velikih problema imao je i s dijeljenjem razlomaka jer nije prihvaćao zakone vezane za njih. Preciznije, nije mogao shvatiti kako dijeleći 2/3 sa 3/4 može dobiti 8/9, što je veći broj od 2/3. Njegovo zaključivanje bilo je ovakvo: ako dijeleći A sa B dobivamo C, onda C mora biti manji od A. Naravno, Leonardov koncept dijeljenja nije sasvim pogrešan, budući da vrijedi pri dijeljenju prirodnih brojeva, no problem je nastao kada ga je nekritički pokušao generalizirati, tj. primijeniti na racionalne brojeve, gdje ne vrijedi. Tada je izmislio drugi način dijeljenja razlomaka koji, nažalost, također nije korektan. Htio je pomnožiti 2/2 sa samim sobom. Što je pritom dobio? Rezultat je u najmanju ruku začuđujući:
iz čega je zaključio da je √2 = 2/2. Generalizirajući ovaj rezultat, tvrdio je da vrijedi √3 = 3/3, √4 = 4/4... Iz svega navedenoga jasno se vidi da je Leonardo imao ozbiljnih teškoća u savladavanju računskih operacija, omjera i osnovnih artimetičkih tehnika. GeometrijaLeonardova saznanja o geometriji vidimo iz Madridskih kodeksa, koji se sastoje od dva dijela te iz kodeksa Forster. Tako možemo uočiti da su ga jako zanimale konstrukcije pravilnih mnogokuta pomoću ravnala i šestara, pri čemu je opseg mnogokuta dijelio na 3, 4, 5, 6, 7, 8, pa sve do 48 sukladnih dijelova. Leonardo je dao i dvije konstrukcije pravilnog peterokuta. Naravno, mnoge od njegovih konstrukcija samo su približne. Suočio se i s problemom konstrukcije kvadrata ako je dan kao suma dvaju kvadrata, dajući pritom samo približnu proceduru. Rijetko je davao objašnjenja svojih konstrukcija, pa izgleda da su proizlazile same od sebe. Leonardo raspravlja i o nejednakosti trokuta, vrijednosti zbroja veličina unutarnjih kutova trokuta te jednakosti vanjskog kuta trokuta i zbroja njemu nasuprotnih unutarnjih. Zanimljivo je da je ta, nama danas elementarna pitanja, genije savladavao tek u dobi od 44 godine. 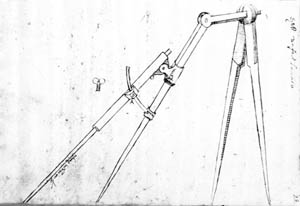
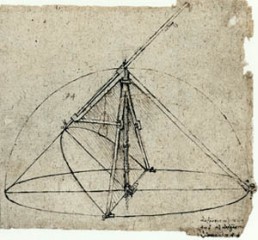

5. Leonardova matematika poslije susreta s PaciolijemBez formalnog obrazovanja i uz to još disleksičan, Leonardo nije bio u stanju čitati tekstove na latinskom i grčkom, što mu je još više odmoglo u savladavanju tadašnje matematičke kulture. Međutim, 1493. godine u Urbinu i 1494. godine u Veneciji napokon izlazi enciklopedija Luce Paciolija Summa de arithmetica, geometrica, proportioni et proportionalita. Tu je knjigu Leonardo odmah kupio i proučio. Tada ga je najviše fascinirao problem kvadrature kruga te teorija lunula. Susret Leonarda i Luce Paciolija dogodio se 1496. godine u Milanu. Tada je započelo i njihovo "matematičko" prijateljstvo. 
ProporcijeVeć od antičkih vremena kipari i slikari tajnu "lijepe estetike" željeli su objasniti uz pomoć matematičkih odnosa. U tome je prednjačio starorimski arhitekt Vitruvije iz čijeg je univerzalnog djela O arhitekturi Leonardo učio o proporcijama ljudskog tijela. Čitajući Vitruvijevo djelo otkrivamo sljedeće proporcije:
Kao rezultat, 1492. godine nastao je poznati Leonardov crtež Vitruvijev čovjek, upotpunjen bilješkama. Na njemu je zorno prikazan lik golog muškarca s ispruženim rukama u dvije pozicije, upisan istodobno u krug i kvadrat. Crtež i tekst ponekad se zovu zakon proporcija ili, rjeđe, proporcije čovjeka. Ovj crtež pruža savršen primjer Leonardova interesa za problematiku proporcija, a prezentira i temelj Leonardovih pokušaja povezivanja čovjeka i prirode. To je bila znanstvena analiza koja je imala kozmološki značaj (povezanost čovjeka i svemira) i umjetnički značaj (pravilna reprezentacija ljudskog tijela i stvaranje arhitekture temeljene na proporcijama ljudskog tijela). Neki znanstvenici vjeruju da kvadrat na Leonardovu crtežu simbolizira materijalnu egzistenciju, a krug duhovnu. Leonardo svojim crtežom očito ilustrira Vitruvijevo djelo O arhitekturi koje objašjava: "Pupak je prirodno smješten u centar ljudskog tijela, i ako muškarac leži licem okrenutim frontalno, a ruke i noge raširene, od pupka kao centar, upisan u krug, ono dodiruje njegove prste ruku i nogu. No, nije samo da je ljudsko tijelo opisano krugom, što se može vidjeti smještajući ga u kvadrat. Za mjerenje od stopala do vrha glave, a zatim preko raširenih ruku, vidimo da su te dvije duljine jednake; pa linije u pravim kutovima jedno od drugoga, okružujući tijelo, tvore kvadrat." 
Naravno, ne postoji univerzalni skup proporcija ljudskog tijela. Antropologija je stvorena s ciljem opisivanja tih individualnih varijacija. Vitruvijeva mjerenja mogu biti interpretirana kao prosječne proporcije ili možda kao opis idealne ljudske forme. Vitruvije prolazi kroz teškoće u matematičkom preciziranju definicije u značenju pupka kao centra tijela, a različite definicije vode do drukčijih rezultata; npr. centar ljudskog tijela ovisi o poziciji krajeva i u stajaćem stavu je najčešće 10 cm niže od pupka, blizu vrha kostiju bokova. Primijetimo da Leonardov crtež kombinira Vitruvijeva saznanja s vlastitom opservacijom tadašnjeg ljudskog tijela. Pri crtanju ispravno primjećuje da kvadrat nema isti centar kao krug, pupak, ali je negdje niže u anatomiji ljudskog tijela. Ova prilagodba inovativan je dio Leonardova crteža i ono što ga razlikuje od ranijih ilustracija. On se također razlikuje od Vitruvijeva crteža crtajući ruke podignute u poziciji u kojoj su vršci prstiju u razini s vrhom glave, dok su kod Vitruvija mnogo više, pri čemu ruke tvore linije koje prolaze kroz pupak. Ovaj crtež često se upotrebljava kao simbol esencijalne simetrije ljudskog tijela i po ekstenziji, i svemira u cjelini. Leonardov Vitruvijev čovjek ostaje do dana današenjeg jedan od najspominjanijih i najreproduciranijih crteža u svijetu. Proporcije ljudskog tijela, kao što je predložio sam Vitruvije, inspirirale su brojne umjetnike u vlastitim verzijama prikaza Vitruvijeva čovjeka. Jedan takav prikaz nalazimo i na kovanici od 1 eura. 
Mnogi geometrijski crteži i osvrti u različtim kodeksima imaju za temu zlatni rez. Međutim, često je račun koji ide uz njih bio neispravan. Za primjer ćemo uzeti problem iz Kodeksa Francuskog instituta u kojem se, kao što je već napomenuto, bavio geometrijom. Leonardo je želio podijeliti segment duljine 12 u omjeru zlatnog reza koristeći se pritom propozicijom iz Euklidovih Elemenata. Pronalazi mjere 4 i 8, aproksimirajući na pogrešan način; precizniji račun daje 4.5835921 i 7.4164079. Točne vrijednosti su iracionalni brojevi o kojima Leonardo nije mogao znati. Konstrukcije šestarom i ravnalomDruga Leonardova omiljena tema spada među klasične probleme geometrije. Stari Grci geometriju su tretirali ravnalom i šestarom; ako je bio postavljen neki konstruktivni problem, njegovo se rješenje tražilo upotrebom samo ravnala i šestara. Zbog toga je došlo do problema pri duplikaciji kocke, kvadraturi kruga i trisekciji kuta. Tek u 19. stoljeću matematičari su dokazali da se ti problemi ne mogu riješiti samo ravnalom i šestarom. Leonardo se u Atlantskom kodeksu pozabavio problemom duplikacije kocke. Problem je vezan uz legendu u kojoj je Delijsko proročište postavilo zahtjev da se oltar u obliku kocke zamijeni drugim, dvostruko većeg obujma. To znači, ako prvobitni oltar ima bridove duljine a, traženi oltar će imati bridove b = ³√2 a. Već iz ovoga možemo naslutiti da će Leonardovo rješenje ovoga problema biti aproksimativno. Zašto? Od Pitagorina vremena znalo se da √2 nije racionalan broj. Stoga su matematičari i arhitekti pokušavali naći racionalne brojeve koji će najbolje aproksimirati broj √2. Već spomenuti Leon Battista Alberti predlagao je da se broj √2 aproksimira sa 7/5. Broj ³√2 nije samo iracionalan, on čak nije niti konstruktibilan ravnalom i šestarom. No, vratimo se Leonardu. U već spomenutom kodeksu dao je "rješenje" problema duplikacije kocke za kocku duljine stranice 4 (dakle volumena 64) i kocku duljine stranice 5 (dakle volumena 125), ustvrđujući da je drugi volumen dvostruko veći od početnog. Danas uz pomoć kalkulatora lako izračunamo duljinu stranice kocke volumena 128, približno jednaku 5.039. S empirijskog gledišta, pogreška je mala i Leonardovo rješenje je prihvatljivo. Bez imalo sumnje, Leonardo je bio majstor aproksimacija kojima je posvetio mnogo pažnje. Jedna od najtrajnijih strasti kojoj je Leonardo posvetio mnogo pozornosti i stranica raznih kodeksa je pitanje kvadrature ravninskih figura omeđenih krivuljama. Pod terminom kvadrature smatra se konstrukcija kvadrata površine jednake površini zadane figure. Ako je pritom riječ o poligonalnoj figuri, problem je lako rješiv. Stvari se počinju komplicirati ako je riječ o figuri omeđenoj krivuljama, što je već poznato iz problema kvadrature kruga. Često iz Leonardovih riječi možemo shvatiti da mu problem nije u potpunosti bio jasan. Poznata je 455. stranica Atlantskog kodeksa koja sadrži oko 180 zadataka preoblikovanja figura unutar kojih upisuje kvadrat u krug dobivajući pritom kružne segmente. U rješavanju problema kvadrature možemo zamijeniti jednu figuru drugom, no pritom njihove površine moraju ostati iste. U Leonardovim rješenjima više je došla do izažaja njegova slikarska mašta nego matematička kompetencija. 
Mnogo pažnje posvetio je i pitanjima vezanima za volumen; podjela piramide na sukladne dijelove, transformacija dodekaedra u kocku jednakog volumena, transforamcija piramide u drugu istoga volumena itd. Kako je izveo kvadraturu dodekaedra? Leonardo je, kako bi izračunao njegov volumen, podijelio poliedar na 12 piramida s peterokutnom bazom, od kojih je svaku nadalje podijelio na 5 piramida trokutaste baze. Svaka od dobivenih piramida zatim je transformirana u paralelopiped, čiji volumen pomnožen sa 60 tvori drugi paralelopiped koji je transfomiran u kocku istog volumena kao dodekaedar. 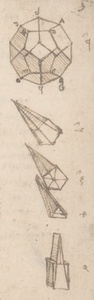
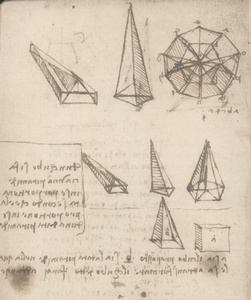
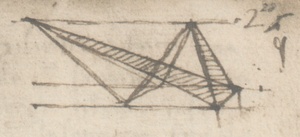
Lunule i kvadratura krugaHipokrat s Khiosa (5. stoljeće prije Krista), možda Pitagorejac, bio je jedan od najpoznatijih geometara tog doba. Riješio je problemom kvadrature nekoliko likova u obliku polumjeseca, zvanih lunule. Uzmimo kao primjer jednakokračan trokut ABC s bazom BC i nasuprotnim vrhom A, upisanog u polukružnicu promjera BC. Ako konstruiramo izvan trokuta polukružnicu promjera AB, tada je lunula dio omeđen njom i prvom nacrtanom polukružnicom. Hipokrat je pokazao da je površina te lunule jednaka polovici površine promatranog trokuta te je na taj način realizirao kvadratru uz pomoć ravnala i šestara. 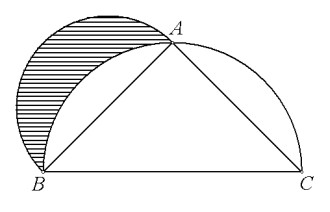
Dakle, na temelju svih znanja koja je primio od Paciolija, Leonardo se napokon počeo baviti matematičkim problemima određene važnosti. Nije na odmet reći da je Leone Battista Alberti napisao djelo O kvadraturi lunule, koje je Leonardo očito čitao. Možda san o kvadraturi kruga, koji je Leonarda pratio tijekom života, upravo nalazi svoje začetke u tom djelu. Problem kvadrature kruga vuče korijene iz antičkih vremena. Grci su već od Platonova vremena znali aproksimirati površinu kruga na različite načine, ali nije im uspijevalo pomoć ravnala i šestara konstruirati kvadrat jednake površine. Tek je 1882. godine Carl Louis Ferdinand von Lindemann (1852. - 1939.) dokazao da je to nemoguće. On je pokazao da je π transcendentan broj, a pomoću ravnala i šestara mogu se konstruirati samo segmenti čija je duljina racionalan broj i neki algebarski iracionalni brojevi. Leonardo, oduševljen kvadraturom lunula i zanesen snom Leonea Battiste, smatrao se sposobnim rješiti problem kvadrature kruga. U mnogim prilikama objavio je da je riješio taj problem, no pritom nigdje nije dao rješenje i konstrukciju. Očito se radilo o približnim rezultatima, dakle aproksimacijama. Arhimed, čija su djela u to vrijeme bila prevedena i došla u Leonardove ruke, izračunao je približnu vrijednost broja π konstruiravši pravilne poligone s 96 strana, upisane i opisane danoj kružnici. Isto je napravio i Leonardo. Poliedri i popločavanja ravnineLeonardo je nacrtao brojne slike poliedara za rukom pisano izdanje Božanskog omjera Luce Paciolija. Pacioli ju je potom darovao Giangaleazzu Sanseverinu i danas se čuva u biblioteci Ambrosiana u Milanu. 
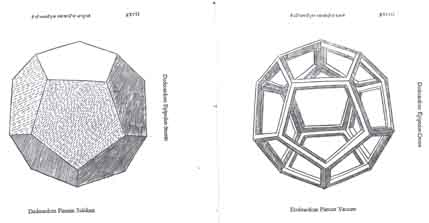
Leonardovo ime matematičari često spominju vezano uz popločavanja ravnine. Pojednostavljeno rečeno, riječ je o problemu prekrivanja ravnine zadanim figurama bez preklapanja i rupa. Ravninu je moguće popločati jednakostraničnim trokutima, kvadratima i pravilnim šesterokutima. 
Više o pravilnim popločavanjima ravnine možete pročitati u članku [KR]. Problem postaje zanimljivijim kada se pravilne pločice zamijene drugim likovima, poligonalnima ili ne. Na brojnim stranicama unutar Atlantskog kodeksa Leonardo crta različita popločavanja ravnine pločicama koje nisu pravilni poligoni. No, imajmo na umu da je ipak riječ samo o crtežima uz koje su bili razni komentari, ali ne i teorijske rasprave. Literatura
Sadržaj: |
