Hrvatski matematički elektronski časopis math.e

Broj 5 











































 

Mario Matijević

Fraktalni oblici u numeričkim aproksimacijama


Sadržaj:

1. Priroda iteracijske metode
2. Cayleyjev problem
3. Koraci algoritma
4. Primjeri fraktalnih bazena
5. Magnetske analogije fraktalnih bazena
6. Optičke analogije fraktalnih bazena
Literatura
Mathematica 5.0 programi (download)

1. Priroda iteracijske metode

Problem traženja rješenja jednadžbe f(x) = 0 prastar je, same metode koje mogu rješavati jednadžbe u formi ax2 + bx + c = 0 poznate su već tisućama godina. U šesnaestom stoljeću talijanski matematičari razvili su egzaktne formule za rješavanje polinomijalnih jednadžbi stupnja tri i četiri, a početkom devetnaestog stoljeća dokazano je kako ne postoje općenite relacije u radikalima za jednadžbe stupnja pet ili više (Niels Abel). Unatoč tome, numeričke metode za rješavanje polinomijalnih jednadžbi bilo kojeg stupnja tijekom povijesti sustavno su razvijane. Sir Isaac Newton (17.st.) razvio je takvu specifičnu iteracijsku metodu, koju je kasnije usavršio Joseph Raphson (17.st.).

Neka je ξ rješenje jednadžbe f(x) = 0 na segmentu [a, b] i neka su df/dx i (d^2f)/dx^2 neprekidne funkcije koje ne mijenjaju predznak na segmentu [a, b]. Ako je xn aproksimacija rješenja, onda možemo naći bolju aproksimaciju tako da uočimo da je

ξ = xn + hn

i da pokušamo ocijeniti hn. Prema Taylorovoj relaciji imamo sljedeće:

f(x_n + h_n) ≈ f(x_n) + h_n df(x_n)/dx= 0,

odnosno   h_n ≈ - f(x_n)/df(x_n)/dx.

Odatle nalazimo novu aproksimaciju:

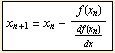x_ (n + 1) = x_n - f(x_n)/df(x_n)/dx      n = 0, 1, 2, ...

Kod konkretnog računa obično vodimo postupak dok ne postignemo |x_ (n + 1) - x_n| = |f(x_n)/df(x_n)/dx| < ε, gdje je ε unaprijed zadana točnost algoritma.

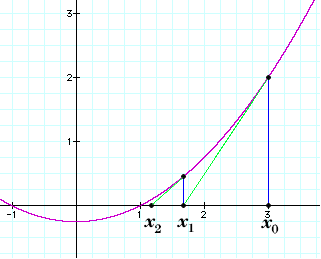
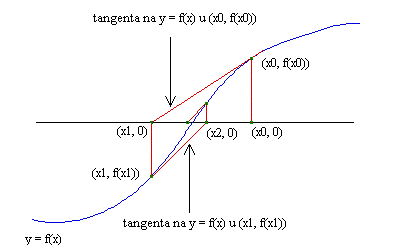
Geometrijska interpretacija metode

Jednadžba tangente u točki T0(x0, f(x0)) glasi

y - f(x_0) = df(x_0)/dx(x - x_0),

a njezino sjecište s x-osi dano je s

x_1 = x_0 - f(x_0)/df(x_0)/dx,

što nam predstavlja točniju aproksimaciju nultočke funkcije.
Iz ovoga opisa jasno je odakle dolazi alternativni naziv metode: metoda tangente. Taj se postupak još zove Newtonov iteracijski postupak ili Newtonova metoda, a ponekad i Newton-Raphsonova metoda.


U sljedećem teoremu dani su dovoljni uvjeti pod kojima postupak konvergira.

Teorem: Neka je f(a)f(b) < 0, neka su   df/dx i (d^2f)/dx^2 različite od nule i ne mijenjaju predznak na segmentu [a, b]. Ako pođemo od neke točke x_0 iz segmenta [a, b] za koju vrijedi

f(x_0)(d^2f(x_0))/dx^2 > 0

i računamo

x_ (n + 1) = x_n - f(x_n)/df(x_n)/dx,     n = 0, 1, 2, ... ,

onda niz {x_n} konvergira jedinstvenom rješenju ξ  jednadžbe f(x) = 0.


Primjer 1: Riješiti jednadžbu e^x = 10 - x na 3 decimalna mjesta.

Rješenje:

f(x) = e^x + x - 10,
df(x)/dx = e^x + 1,
x_ (n + 1) = x_n - (e^x_n + x_n - 10)/(e^x_n + 1).

Lako ocijenimo da je f(0) < 0,   f(1) < 0,   f(2) < 0, ali   f(3) > 0.
Time znamo da je rješenje iz [2, 3]. Izborom početne aproksimacije x_0 = 2 dobivamo sljedeće aproksimacije:

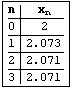
n x_n 0 2 1 2.073 2 2.071 3 2.071


Primjer 2: Neka je zadani polinom p(x) = x^3 - x. Nađimo nultočke koristeći se Newtonovom metodom.

Rješenje:

[Graphics:index_52.gif]

   - nultočke polinoma p redom su -1, 0 i 1.
    - iteracijski postupak glasi:

x_ (n + 1) = x_n - p(x_n)/(p ' (x_n)) = x_n - (x_n^3 - x)/(3 x_n^2 - 1) = (2 x_n^3)/(3 x_n^2 - 1) .

Ako za početnu aproksimaciju uzmemo x_0 = 0.25, tada slijedi niz aproksimacija:

n x_n 0 0.25 1 -0.0385 2 0.000114 3 -0.299*10^(-11)

Kao što se vidi, za početnu vrijednost blizu nultočke konvergencija je jaka te završava u malom broju iteracija.
Ako bismo sada za početnu vrijednost uzeli npr. x_0 = 0.75, dobili bismo sljedeći niz aproksimacija:

n x_n 0 0.75 1 1.227 2 1.051 3 1.003

Opet, kao i u prethodnom slučaju, niz uzastopnih aproksimacija konvergira u jako malom broju koraka prema najbližem korijenu. Pretpostavimo sada da je početna aproksimacija x_0 = 0.45 (uočite da je blizu polovice udaljenosti između nultočaka 0 i 1) pa nam iteracijski algoritam daje sljedeći niz aproksimacija:

n x_n 0 0.45 1 -0.464 2 0.567 3 -10.056 4 -6.793 ... 7 -2.135 8 -1.536 9 -1.192 10 -1.038 11 -1.002

Opet nastupa konvergencija, ali je očito da nije brza kao u prošlom slučaju te se već sada mogu naslutiti mane Newtonove metode. U većini slučaja algoritam će pronaći nultočku, ali ona ne mora biti nužno najbliža početnoj aproksimaciji; npr. da smo u prošlom primjeru umjesto x_0 uvrstili 0.46, niz iteracija bi konvergirao prema 1. Očito je da je važna karakteristika ove metode "osjetljivost na početne uvjete", što je jako važno svojstvo svakog kaotičnog dinamičkog sustava, gdje se onda najčešće u vizualizaciji problema javljaju fraktalni uzorci.
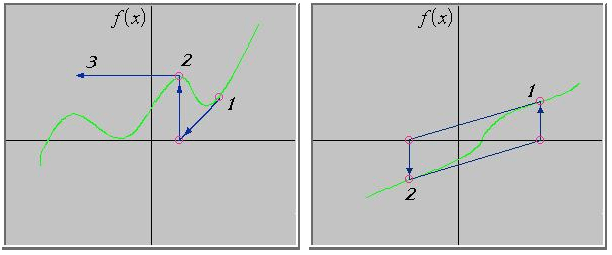
Osim spomenutih mana postoje situacije kada je ova metoda potpuno nekorisna:

    (1) ako bismo za početnu aproksimaciju uzeli točku koja se nalazi točno na granici između dvaju rješenja, tada bi tangenta u točki (x_0, f(x_0)) bila paralelna s x-osi te bismo dobili izrazito jaku divergenciju jer nazivnik u iteracijskoj metodi postaje nula.

    (2) općenito, ovaj se problem javlja u svim ekstremima funkcije f(x) jer u nazivniku iteratora imamo df(x)/dx; stoga svaka aproksimacija stacionarnom točkom (gdje f(x) ima ekstrem) daje kaotično ponašanje iteracijskog procesa.

Primjeri mogućih problema iteracijske metode, kada imamo prelazak u kaotični režim rada (divergencija metode):



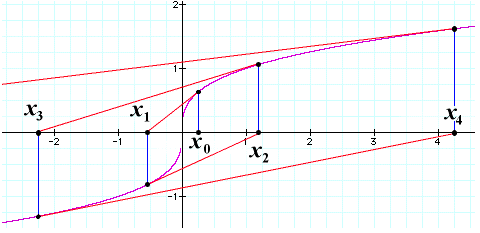
(početne aproksimacije uzrokuju kaotično ponašanje iteracijske metode)

    


2. Cayleyjev problem

Postoji mnogo različitih klasa dinamičkih sustava: kaos u diferencijalnim jednadžbama, razni populacijski modeli u biologiji, fizici i medicini koji služe za simulaciju prirodnih procesa i sl. No, u slučaju kada je iteracijski proces (tzv. transition function) nekog sustava polinom ili racionalna funkcija s kompleksnom varijablom, tada je matematička pozadina dana upravo teorijom Juliaovog skupa.
Naziv "Juliaov skup" potječe od francuskog matematičara Gastona Julie (1893.-1978.), koji je većinu razmatrane teorije razvio u bolnici oporavljajući se od teških rana zadobivenih u Prvom svjetskom ratu. Za vrijeme napada Nijemaca na francusku frontu obrane (1915.) Julia je izgubio nos te je do kraja života nosio kožni povez preko lica. Njegovi rani radovi ostali su zaboravljeni dugi niz godina, sve do početka 1980. kada se pojavio Benoit Mandelbrot, koji je nastavio graditi teoriju.

Arthur Cayley Gaston Julia Benoit Mandelbrot
Arthur Cayley (1821.-1895.) Gaston Julia (1893.-1978.) Benoit Mandelbrot (1924. -)

Ogroman napredak koji je Julia postigao u proučavanju nelinearnih kompleksnih dinamičkih sustava  dobiva još i više na važnosti kada se uzme u obzir da u to vrijeme nije bilo računala: umjesto toga sve je bilo prepušteno imaginaciji i matematičkoj intuiciji. Većina njegova rada bila je motivirana člankom poznatog engleskog matematičara sir Arthura Cayleya. Članak je publiciran 1879. pod nazivom "Newton-Fourier Imaginary Problem". Problem je bilo traženje proizvoljnih točaka (skupova) kompleksne ravnine u kojima Newtonova metoda uspješno konvergira prema nultočkama kompleksnog polinoma f(z) = z^3 - 1.

Newton-Fourier Imaginary Problem

Nultočke promatrane funkcije ponašaju se kao magneti za proces iteracije (vidi analogije u magnetizmu). Cayley je uzeo sljedeći primjer kao bi pokazao problem nalaženja tzv. "privlačnih bazena" koje stvaraju nultočke funkcije kompleksne varijable.
Funkcija f(z) = z^2 - 1 ima dva korijena: z = 1 i z = -1.
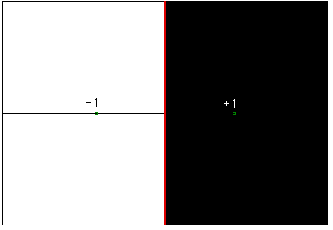
Označimo bazene privlačnosti tih korijena s A(+1) i A(-1), tj. A(+1) je skup svih točaka ravnine koje pod djelovanjem Newtonove metode konvergiraju prema +1, a A(-1) je skup svih točaka koje konvegriraju prema -1. Cayley je uspio matematički dokazati sljedeće:

A(-1) je lijeva polovica kompleksne ravnine,
A(+1) je desna polovica kompleksne ravnine.

Na slici sve crne točke konvergiraju prema +1, a sve bijele prema -1.

-1 +1

Možemo očekivati da će nultočke (+1) i (-1) jednakom snagom privlačiti točke na crvenom vertikalnom pravcu pa one zapravo neće uopće konvergirati pod djelovanjem metode. Ta linija predstavlja kaotični režim rada Newtonove metode, tj. općenito možemo reći da se uvijek na granici privlačnih bazena odvija kaotična dinamika sustava.
Nakon riješenog prethodnog primjera, Cayley je pokušao riješiti posve analogan problem, gdje je stupanj polinoma uvećan za jedan, tj. f(z) = z^3 - 1.
Funkcija kompleksne varijable  f(z) = z^3 - 1 ima tri korijena koja su raspoređena na jediničnoj kružnici tako da tvore vrhove istostraničnog trokuta (de Moivreova formula):

z_1 = 1, z_2 = (-1/2 + 3^(1/2)/2 i), z_3 = (-1/2 - 3^(1/2)/2 i).

Te su nultočke ekvidistantni kompleksni brojevi te im se argumenti razlikuju za višekratnik od 120º. Prirodno bi bilo zaključiti, na temelju prethodnog primjera, da će svaki privlačni bazen biti kružni isječak s centralnim kutem od 120° kako je prikazano na slici dolje:

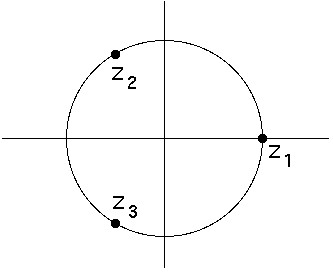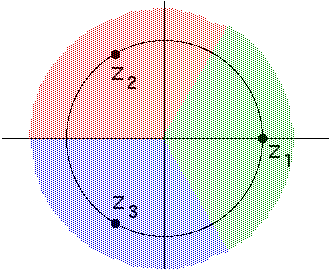(nultočke funkcije) (krivi bazeni)

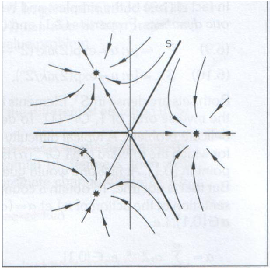(krive granice)

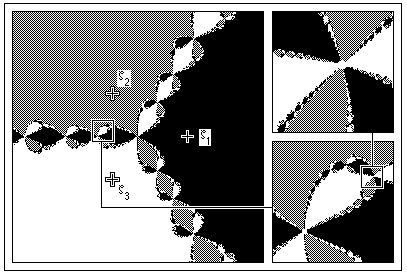Međutim, to je potpuno pogrešno i to je Cayley znao. On nije uspio za života riješiti promatrani problem zato što je rješenje iznimno komplicirano, kao što možemo vidjeti na slikama:

(ksi_1, ksi_2, ksi_3 → nultočke funkcije z^3 - 1)

(3D prikaz sa pridruženom iteracijom na z-osi)

    - crne točke: područje konvergencije prema 1
    - sive točke: područje konvergencije prema (-1/2 + 3^(1/2)/2 i)
    - bijele točke: područje konvergencije prema (-1/2 - 3^(1/2)/2 i)

Julia je shvatio da tri odgovarajuća bazena privlačnosti imaju zajedničku granicu! Granica između privlačnih bazena ekstremno je komplicirani objekt: granica se sastoji od točaka koje se istovremeno nalaze u svim trima područjima (tzv. three corner point). Iako bazeni sami po sebi nisu fraktalni - oni sadrže velike skupove bez ikakve podstrukture - njihove granice imaju fraktalna obilježja. Uvećanjem malog komadića granice dobivamo opet istu strukturu sadržanu samu u sebi (obilježje samosličnosti) i tako dalje u beskonačnost.
Ta granica ima fraktalne osobine i to je zapravo Juliaov skup (fraktal)! Krenuvši od bilo koje točke na granici bazena, uvijek dobivamo prijelaz iteracijskog procesa u kaos.

Newton dance
(promjena oblika fraktalnih granica ovisno o relativnom položaju nultočaka polinoma stupnja 3)


3. Koraci algoritma

Ako se Newtonova metoda poopći na kompleksnu ravninu, gdje se ona sustavno provodi za svaku točku promatranog uzorka C-ravnine za neki zadani polinom, tada dobivamo grafičku interpretaciju problema, gdje se kao direktna posljedica mana (karaktera) iteracijske metode javljaju fraktalni uzorci. Sama priroda kompleksnog (pa i realnog) iteratora izrazito je osjetljiva na početne uvjete te se on može promatrati u kontekstu dinamičkog sustava, gdje je njegovo buduće stanje definirano sadašnjim stanjem uz neke dodatne uvjete i parametre. Poopćenje problema na kompleksnu ravninu generira uistinu fascinantne fraktalne skupove, koji su realizirani programskim paketom Mathematica 5.0 u sljedećim programskim koracima:

- korisnik učitava proizvoljni polinom u kompleksnoj varijabli z kao ulazni parametar

- algoritam nalazi nultočke polinoma i polove iteracijske metode te ih u različitim bojama smještava unutar C-ravnine

- sve kompleksne točke koje se nalaze u neposrednoj blizini nultočaka u relativno malom broju iteracija konvergiraju (teže prema korijenu), tj. možemo reći da je kriterij konvergencije ispunjen ako je apsolutna udaljenost aproksimacije od stvarnog korijena (ε = zadana točnost) ε < 10^(-4), a sve ostale točke koje u rastu iteracije ne ispunjavaju taj uvjet, tretiramo kao divergentne. U tu svrhu moramo imati predefiniranu vrijednost maksimalne iteracije koja služi kao prekidni parametar jer točke koje ulaze u stanje kaosa nikada se neće približiti (kaotično osciliraju unutar ravnine) nijednoj nultočki, pa bismo dobili beskonačnu petlju unutar potprograma

- boja se kompleksnoj točki ("pikselu") može pridružiti na dva osnovna načina:

Kriterij konvergencije: svaka nultočka polinoma ima svoju jedinstvenu boju, što znači da svaka točka koja u iteracijskom procesu konvergira, ima upravo boju korijena prema kojem konvergira, a sve ostale (divergentne) točke imaju svoju nezavisnu boju. Globalno promatrajući, koliko imamo nultočaka polinoma, toliko ćemo imati i različitih fraktalnih bazena u kompleksnoj ravnini.

Kriterij iteracije: iteracija potrebna da bi točka dosegla svoje konačno stanje ("kaos" ili "red") predstavlja boju pri ispisu, uvažavajući činjenicu da je zapravo iteracija limitirana nekim maksimalnim iznosom. Fraktalni skup realiziran na ovaj način daje globalni uvid u brzinu promjene kompleksnog dinamičkog sustava na promatranom uzorku C-ravnine.

- oblik fraktalnog skupa definiran je mnogim parametarima: kompleksnim polinomom, maksimalnim brojem iteracija, zadanom točnošću ε, veličinom uzorka C-ravnine i sl., no ono što ostaje kao univerzalno obilježje za bilo koji polinom jest kaos koji se uvijek javlja na granici bazena privlačnosti i u polovima iteratora.

4. Primjeri fraktalnih bazena

Primjenimo Newtonovu metodu na polinomu f(z) = z^4 - 1 koristeći se Wolframovim programom Mathematica 5.0:

    - kompleksni iterator je po definiciji:   z_ (n + 1) = z_n - f (z_n)/(f ' (z_n)) = z_n - (z_n^4 - 1)/(4 z_n^3) = (3 z_n^4 - 1)/(4 z_n^3)

    - nultočke polinoma su redom 1, -1, i, -i

    - kaos se očituje na simetralama (I-III) i (II-IV) kvadranta jer su upravo to točke koje su na jednakim udaljenostima od gore navedenih nultočaka

    - pol kompleksnog iteratora u središtu je kompleksne ravnine (to je pol reda 3, izrazito jaka divergencija)

Nakon što smo pokrenuli program, koji je priložen za download kao Mathematica5.0 Notebook, dobivamo sljedeće:

(a) boja se točki dodjeljuje prema kriteriju konvergencije:

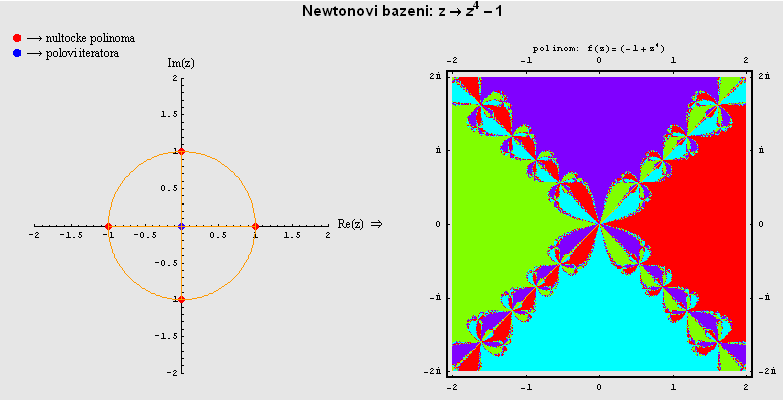
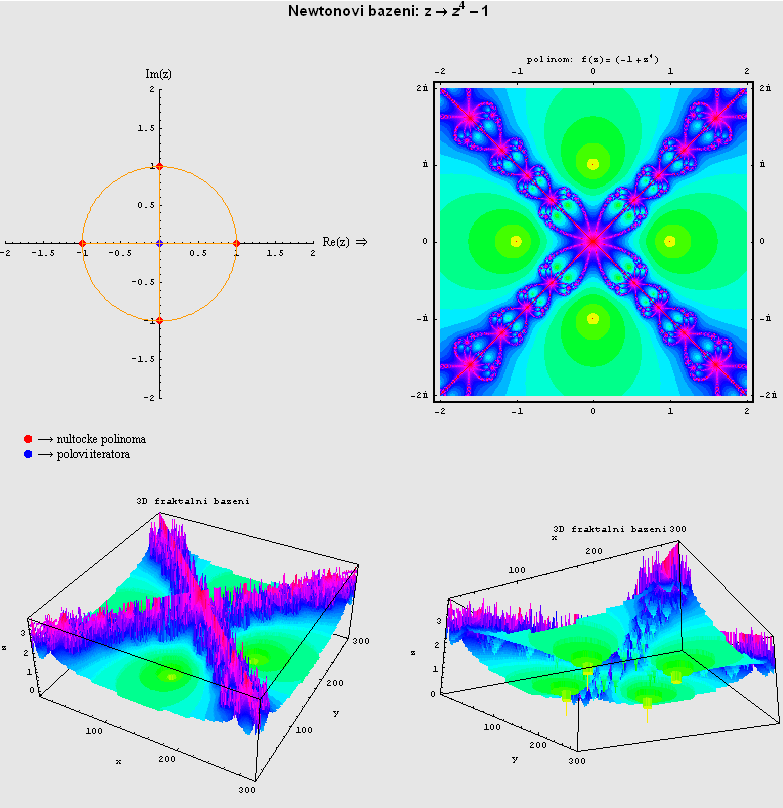
(b) boja se točki dodjeljuje prema kriteriju iteracije:


Trodimenzionalni prikaz dinamike sustava (3D fraktalni bazeni)

Svakoj točki kompleksne ravnine pridružena je konačna iteracija kao funkcijska vrijednost na z-osi, koja predstavlja upravo onu iteraciju na kojoj možemo donijeti zaključak o karakteristici točke: ili će konvergirati prema jednoj od nultočaka funkcije (tu je iteracija manja od maksimalne) ili će kaotično oscilirati unutar ravnine (tu je iteracija upravo jednaka maksimalnoj iteraciji - to je prekidni parametar!).
Valja uzeti u obzir da je na z-osi 3D prikaza zapravo korišten prirodni logaritam iteracije zbog što boljeg raspršenja vrijednosti unutar jediničnog intervala (koristi se ugrađena funkcija Hue[x], gdje je x logaritam iteracije), što za posljedicu daje finije prijelaze boja. Na gornjim dijagramima dobivamo jasnu interpretaciju fraktalnih bazena ("stepenice" su iteracije skalirane s ln(x)).
Točke relativno blizu korijenima brzo dostižu konvergenciju te se očituje grupiranje boja s porastom iteracije, npr. crvene točke (vidi gore) su korijeni koji postižu konvergenciju u 1. iteraciji metode, žute točke su sve točke koje to postižu u 2. iteraciji, zatim slijedi nijansa zelene boje, što je konvergencija u 3. iteraciji itd., pa sve do ljubičaste, koja predstavlja divergenciju s maksimalnim brojem iteracija (u programu je maksimalan broj iteracija 150). Upravo na tu kaotičnu regiju otpada najveći dio procesnog vremena jer je to slučaj kada algoritam mora za svaku točku proći maksimalan broj puta kroz petlju da bi se ona terminirala prekidnim parametrom - maksimalnom iteracijom.

Neki primjeri prostornog prikaza iteracije za f(z) = z^4 - 1:

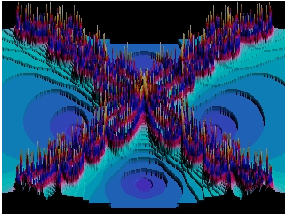(pogled odozgo) (pogled pod kutom od 45° prema C-ravnini)

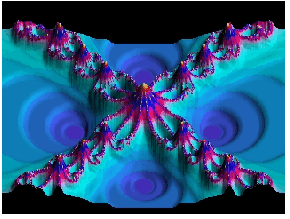(kao prethodni, ali uz interpolaciju)

Primjer 3D prikaza fraktalnih bazena za funkciju kompleksne varijable :

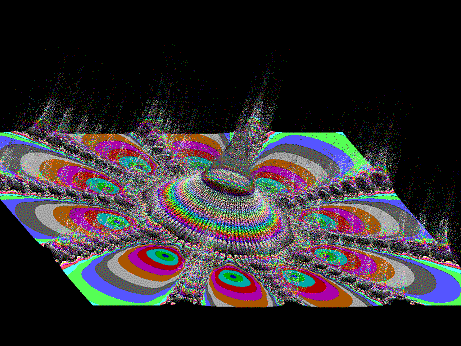(visina točke jest apsolutni iznos iteracije)

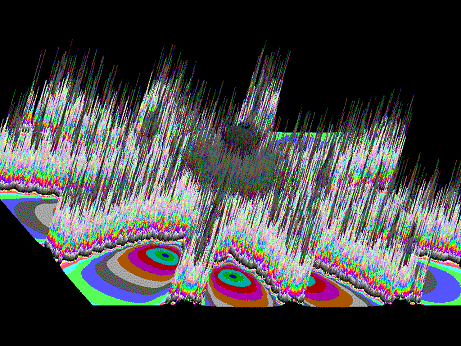(duljina "šiljaka" jest apsolutni iznos iteracije)

Primjer uvećanja područja oko pola iteratora za funkciju (z = 0 je pol reda 9):

Primjer 3D formi za f(z) = z^4 - 1:

(pogled odozgo) (koso pod 45º)

(pogled u razini ravnine kako bi se istaknula iteracija) (kompleksna ravnina zatvorena u sferu)

Orbita kompleksne točke-dinamika sustava

Ovo je kratki opis sekcije koju sadrži priloženi program za download.

Ovdje je relativan položaj točke u iteracijskom procesu prikazan kao funkcija iteracije te se na temelju toga stvara animacija putanje točke u ravnini pod djelovanjem kompleksnog iteratora. Odabir točke sa skupa, kojoj želimo promotriti orbitu, radi se pomoću miša: pogledajte upute u izborniku Input-Get Graphics Coordinates u Mathematica 5.0.

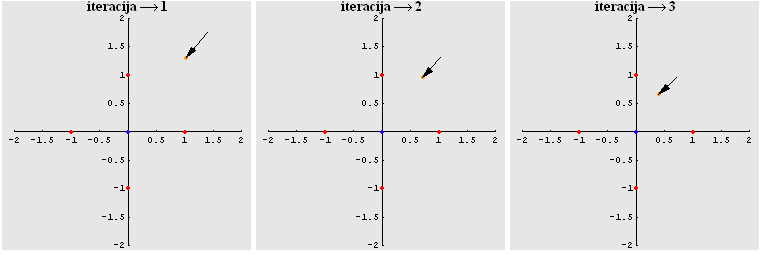(itd. sve do kritične iteracije)

Zanimljivo je promotriti dinamičko ponašanje točaka za npr. f(z) = z^4 - 1, koje leže točno na granicama fraktalnih bazena. One se u rastu iteracije približavaju polu, klizeći točno po simetralama kvadranata, koji ih odbacuje relativno daleko no nakon dovoljnog broja iteracija vraćaju se natrag i ciklički ponavljaju gibanje. Te točke pod djelovanjem iteracijskog algoritma zapravo izvode skok iz jednog u drugi kvadrant (I→III ili II→IV), tako da im je gibanje ograničeno samo na simetralu.

Također, uvedena je i tzv. "kružna orbita": točka u iteracijskom procesu predstavljena je kružnicom kojoj je radijus recipročna vrijednost kvadrata iteracije (kvadrat iteracije uzima se zbog bržeg smanjenja kružnice - vizualno je bolje predočena konvergencija). Ovaj način prikaza pogodan je za promatranje privlačnih točaka ravnine - nultočaka polinoma ("basin of attraction").

Primjer kružne orbite za polinom stupnja 5:

 
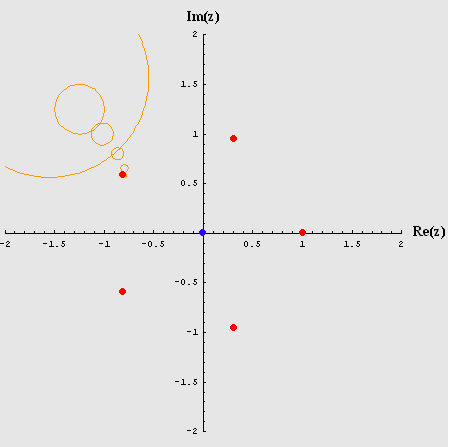(očito je da iteracijski proces za promatranu točku konvergira prema nultočki u II. kvadrantu)

Primjer kružne orbite za točku (1+ i) na granici bazena ( f(z) = z^4 - 1):

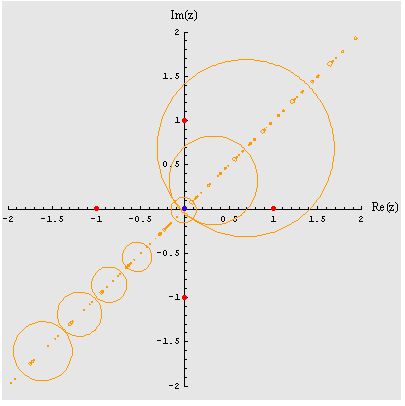(ovdje je radijus kružnice recipročna vrijednost iteracije)

"Zoom explorer" - fraktalna obilježja

Namjena ove sekcije jest vizualizirati osnovne karakteristike fraktalnih uzoraka kao što su samosličnost i beskonačna složenost, koje korisnik može istražiti unutar skupa na proizvoljnom mjerilu. Algoritam prima na ulazu dvije varijable: centar i faktor uvećanja.
Centar uvećanja je točka koju korisnik zadaje mišem s osnovnog fraktalnog skupa te predstavlja centar uvećanog uzorka C-ravnine u formi kvadrata. Faktor uvećanja jest broj koji govori o jačini uvećanja, a on je definiran kao polovica stranice spomenutog kvadrata. Očito je da što je faktor uvećanja manji broj, to dobivamo snažniji zoom.
Unutar sekcije su dva interaktivna gumba: reset i magnify. Kako je moguće uvećanje osnovnog skupa, tako je moguće i uvećanje uvećanog skupa, itd., stoga reset služi za resetiranje na veličinu osnovnog uzorka. Za svaki uvećani uzorak program daje ispis svih navedenih parametara, zajedno s veličinom novog uzorka ravnine.

Primjeri:

(z^5 - 1 = 0)

(z^4 - 1 = 0)

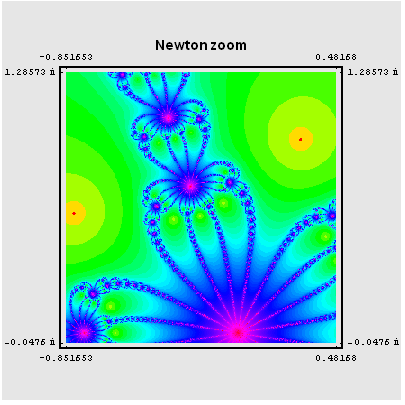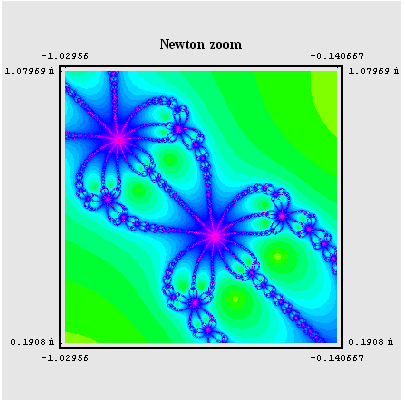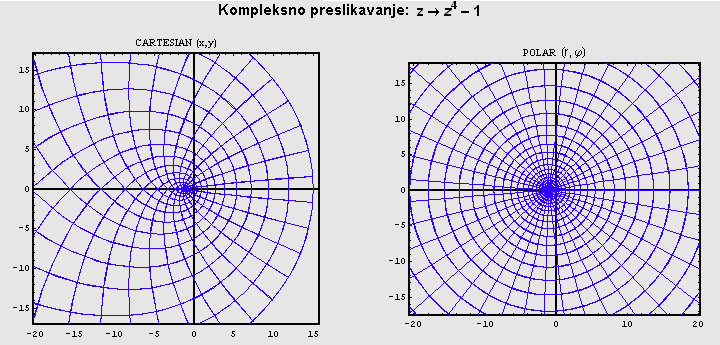
Kompleksno preslikavanje

Kao dodatak priložena je sekcija o kompleksnom preslikavanju, tako da korisnik ima potpuni uvid u svojstva zadanog polinoma. Uzimajući u obzir da je graf funkcije kompleksne varijable 4D-objekt, metodom kompleksnog preslikavanja možemo vidjeti u što će se preslikati mreža početnog uzorka C-ravnine pod djelovanjem zadanog polinoma.
Početni koordinatni sustav ima dimenzije kvadrata [-2, 2]×[-2i, 2i], što je označeno na osnovnom fraktalnom skupu.

Pogledajmo neke osnovne definicije.

Neka je G 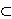C područje i  f : G → C zadana funkcija. Za f kažemo da je funkcija kompleksne varijable. Obično pišemo w = f(z) te kažemo da f preslikava točke kompleksne z-ravnine u točke kompleksne w-ravnine.
Neka je w = f(z). Prikažimo z i w u algebarskom obliku:

z = x + iy,
w = u + iv.

Tada su u i v realne funkcije dviju varijabli (x, y) i funkcija f je potpuno određena parom realnih funkcija (u, v):

w = f(z) = f(x + iy) = u(x, y) + iv(x, y).

Ponekad je prikladnije prikazati argument z u eksponencijalnom obliku, koristeći se Eulerovom relacijom: z = re^(i*phi).
U tom slučaju u i v postaju funkcije dvaju realnih argumenata (varijabli) r i φ. Također, ako w prikažemo u trigonometrijskom obliku, w = Re^(i*phi), slijedi:

w = f(z) = f(x + iy) = R(x, y)e^(i*Phi(x, y))
w = f(z) = f(re^(i*phi)) = R(r, φ)e^(i*Phi(r, phi)

Unutar programa prikazana su dva tipa koordinatnih sustava: kartezijev (x, y) te polarni (r, φ).


5. Magnetske analogije fraktalnih bazena

Pogledajmo klasični fizikalni primjer na kojemu možemo vizualizirati ovaj tip kaosa. Fizikalni analogon Newtonovoj metodi primijenjenoj na funkciju f(z)= z^3 - 1 jest njihalo na koje je obješena metalna kuglica koja se nalazi u simetričnom polju od 3 jednaka magneta (magneti se nalaze u vrhovima istostraničnog trokuta, tj. općenito u vrhovima pravilnog n-terokuta za n-magneta). Svaki magnet predstavlja dominantnu točku privlačenja unutar ravnine - analogno fraktalnom bazenu koji stvara nultočka u kompleksnoj ravnini.

Općenito, gibanje njihala nepravilno je i nepredvidivo s obzirom na početni položaj iz kojeg se njihalo ispušta, ali u konačnici će se smiriti iznad jednog od triju magneta zbog utjecaja trenja (trenje s molekulama zraka, u ležaju i sl.) koje uzrokuje prigušene oscilacije.
Mogli bismo predviđati koji će magnet u konačnici privući kuglicu: za neke inicijalne položaje pouzdano možemo predvidjeti ishod, ali za neke je to posve nemoguće. Magneti se međusobno natječu u dominaciji nad svim točkama ravnine, stoga je teško vizualizirati na koji je način ravnina podijeljena između njih. Zapravo, najviše nas zanima područje vezano uz granicu magneta, koje ima najzanimljivija svojstva.

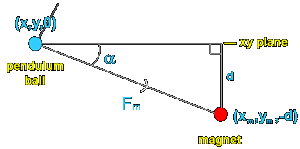
Pokušajmo prvo doći do matematičkog modela njihala uz neka razumna pojednostavljenja:

    - duljina njihala velika je u odnosu na razmak između magneta → tom pretpostavkom možemo reći da se kuglica zapravo giba duž ravnine iznad magneta, a ne po sferi velikog radijusa

    - magneti su točke privlačenja, pozicionirani u vrhovima istostraničnog trokuta koji se nalaze na maloj visinskoj udaljenosti od ravnine duž koje se giba kuglica

    - privlačna sila pojedinog magneta koja djeluje na kuglicu obrnuto je proporcionalna kvadratu udaljenosti od magneta (Coulombov zakon)

Matematički model ovoga problema sustav je od dviju diferencijalnih jednadžbi drugoga reda, rješenje kojih opisuje gibanje njihala duž osi x i y kao funkcije nezavisne varijable - vremena. Sustav će imati karakteristično oscilatorno ponašanje ovisno o iznosu konstante trenja i konstante njihala, koje se javljaju kao parametri u diferencijalnim jednadžbama.

               

Pretpostavimo da se njihalo nalazi na poziciji (x,y,0), a da se magnet nalazi u (x1,y1,-d), gdje je d očito visinski razmak između magneta i njihala. Prema Coulombovom zakonu pretpostavljamo da je privlačna sila po svojim osobinama tzv. "sila inverznog kvadrata", tj. obrnuto proporcionalna kvadratu udaljenosti između magneta i njihala u prostoru:

F_1 ≈ 1/((x_1 - x)^2 + (y_1 - y)^2 + d^2),

gdje su općenito koordinate magneta dane s (x_i, y_i).
Uzimajući u obzir da promatramo gibanje kuglice duž ravnine xy na visini d iznad magneta, moramo projekciju prostorne sile na xy-ravninu množiti s kosinusom, tj. sinusom kuta, kako bismo dobili komponente sile duž osi x i y. Kako je ovo model realnog (otvorenog) sustava, moramo također uzeti u obzir i utjecaj sljedećih parametara:

    - gravitacija: stvara dodatnu silu u xy-ravnini koja vraća kuglicu i ima usmjerenje prema ishodištu,

    - trenje: stvara prigušnu silu kojoj su komponente proporcionalne brzini kuglice u x i y smjeru, tj. vremenskoj derivaciji x(t)-a i y(t)-a.

Uz korištenje drugog Newtonovog postulata, koji kaže da je vremenska promjena količine gibanja upravo proporcionalna rezultantnoj sili i ima usmjerenje kao sila (d/dt(mv) = F_i), dobivamo sljedeći sustav diferencijalnih jednadžbi:

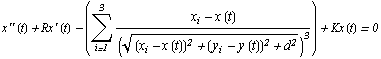
x''(t) + Rx'(t) - (x_i - x(t))/(((x_i - x(t))^2 + (y_i - y(t))^2 + d^2)^(1/2))^3) + Kx (t) = 0
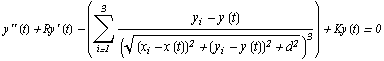y''(t) + Ry'(t) - (y_i - y(t))/(((x_i - x(t))^2 + (y_i - y(t))^2 + d^2)^(1/2))^3) + Ky (t) = 0.

Njihovo potpuno rješenje zahtijeva dva početna uvjeta kako bismo iz fundamentalnog skupa rješenja odvojili fizikalno prihvatljiva od matematički mogućih rješenja.
Početni uvjeti su:

    1. početni položaj kuglice (x(t = 0), y(t = 0))

    2. početna brzina kuglice (x'(t = 0), y'(t = 0)), koja se zbog jednostavnosti uvijek uzima kao 0.

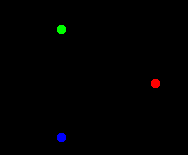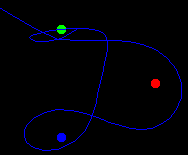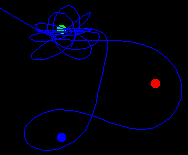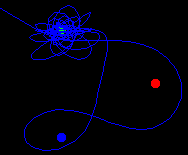
Dodijelimo magnetima boje: plava, crvena i žuta. Iz proizvoljnog položaja pustimo njihalo te će se ono u konačnici smiriti iznad jednog od triju magneta. Ako svaku točku ravnine promatramo kao početnu točku iz koje puštamo njihalo i ako upravo toj točki dodijelimo boju prema magnetu iznad kojeg će se njihalo u konačnici smiriti, tada dobivamo neku vrstu tranzicijskog dijagrama (mape), koji očito ima fraktalnu strukturu (slika dolje desno).
Promotrimo eksperiment (uz zadani faktor trenja R i konstantu njihala K) gdje početni položaji (x(0), y(0)) variraju preko cijelog područja ravnine unutar kojeg se nalaze magneti.

Tada se dobiva tranzicijski dijagram oblika:

   
(magneti = nultočke)   (početni položaj kao osjetljivost na početne uvjete sustava)

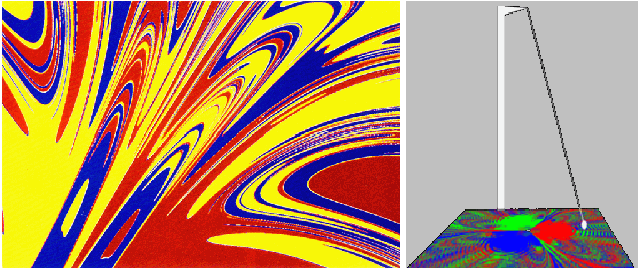           (Cantorov skup uočava se na granicama)                                                         (tranzicijska mapa)

Iako se na prvi pogled čini da su granice sastavljene od svega nekoliko segmenata linije, njihovim uvećanjem možemo vidjeti da imaju sasvim specifična svojstva: to su zapravo izrazito komplicirane strukture koje su jako slične Cantorovom skupu, posebnoj formi fraktalnog skupa. Drugim riječima, bez ulaženja u matematičke formalnosti, gdje god se spajale dvije linije boja, dovoljnim uvećanjem možemo pronaći i treću između njih i tako dalje u svim mjerilima. To obilježje nije ništa drugo nego posljedica osjetljivosti sustava na početne uvjete. Granice, dakle, nisu jasno definirani objekti; one se tvore beskonačnim dijeljenjem linija - ovakvo geometrijsko svojstvo prvi je istraživao (u malo drugačijoj formi) Georg Cantor 1882. Ovisno o početnom položaju kuglice, mi općenito ne možemo predvidjeti ishod zbog preklapanja utjecaja pojedinih magneta, no ono što sigurno možemo predvidjeti za sve sustave ovakvog tipa jest kaos točno na granicama između fraktalnih bazena (magnetskih polja) jer je to područje jednake snage privlačnosti svake nultočke (magneta). Svaka granična točka ima svojstvo da u njezinoj proizvoljno maloj okolini možemo naći točke koje se istovremeno nalaze u svim bazenima privlačnosti.

(primjer s 4 magneta: slijed uvećanja od gore lijevo prema dolje desno otkriva Cantorov skup)

Realizacija magnetskih analogija u programu Mathematica 5.0

Primjer njihala s 3 magneta i početnim položajem kuglice x(0)=1.0, y(0)=1.5:

 

 
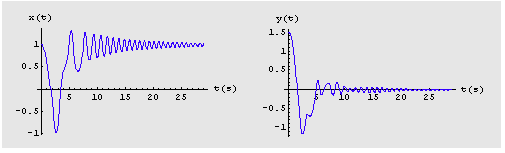(vremenski odziv sustava)

 

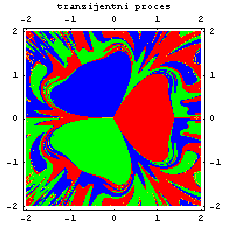Vremenski odziv sustava daje nam gibanje njihala duž osi x i y kao funkciju vremena, a gore je prikazan tranzijentni dijagram koji pokazuje obilježja Cantorovog skupa na granicama. Treba spomenuti veliku složenost algoritma za nalaženje tranzijentne mape: u našem primjeru to je matrica reda 150*150 = 22500 elemenata, tj. točaka ravnine, gdje za svaku pojedinu točku (budući da ona predstavlja početnu vrijednost) moramo nanovo riješiti sustav diferencijalnih jednadžbi, općenito numeričkim metodama!
Velike zatvorene površine (crvena, plava i zelena) ukazuju na stabilnost procesa - ovdje sustav nije osjetljiv na početne uvjete te možemo sasvim lako odrediti ishod.

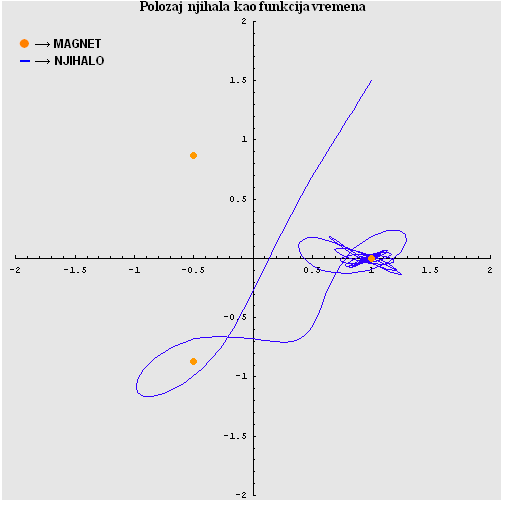x(0) = 1.0, y(0) = 1.5


6. Optičke analogije fraktalnih bazena

Sljedeći primjer je kaos u optici (tzv. "Wada fraktali").
Sastavimo prostorni tetraedar od metalnih kugli (ili npr. ukrasnih kuglica za bor) koje se međusobno dodiruju.


Na zadnjoj slici unutar kugli pojavljuje se fraktalna struktura prirode zbog mnogostrukog preslikavanja refleksija svjetlosti (ovaj pokus još se zove i optički labirint, eng. optical gasket).
Sada iza kugli postavimo reflektirajuće ploče u različitim bojama kako bismo te iste boje dobili unutar kugli na svim mjerilima - to su fraktalni bazeni, tj. područja stabilnosti - pomoću njih ćemo vizualizirati kaotične granice i granične točke.

Ako se laserska zraka usmjeri točno na žuto područje unutar kugli (slika gore desno), tada ona izlazi iz konstrukcije točno na žutu ploču! Zapravo, ona se reflektira beskonačno mnogo puta između kugli i nalazi se unutar svake refleksije unutar svakog žutog bazena. Mogli bismo neformalno reći da u tom slučaju laserska zraka zaposjeda samo 1/3 fraktalne strukure, tj. zaposjeda jedan od moguća tri bazena. Nasuprot tome, ako se laserska zraka usmjeri točno na ono što izgleda kao kaotična granica između žutog i plavog područja, tada ona izlazi iz konstrukcije na sve strane, padajući i na plavu, žutu i zelenu ploču - još jednom vidimo smisao granične točke koja istovremeno leži u svim trima fraktalnim bazenima! U tom slučaju laserska zraka u potpunosti zaposjeda fraktalnu strukturu, ona se nalazi na svim mjerilima unutar svega!

Primjer: Laserska zraka usmjerena točno na fraktalnu granicu predstavlja "graničnu točku", fraktalna struktura u potpunosti je ispunjena laserom.

(vizualizacija granične točke)


Literatura

[1]   Mathematica 5.0 (Wolfram Research)

[2]   "Fractint" - fraktalni generator

[3]   Pendulum Fractal Basin Boundary, Yale University

[4]   Optical Basin Boundaries, Yale University

[5]   P. Bourke: Fractals, Chaos

[6]   R. A. Holmgren: A first course in discrete dynamical systems, Springer, 1996.

[7]   I. Ivanšić: Numerička matematika, Element, 2002.

[8]   D. E. Joyce: Newton Basins

[9]   H. O. Peitgen, H. Jurgens, D. Saupe: Chaos and fractals-New frontiers of science, Springer, 2004.

[10]   R. Robert: Wada Fractals Expo

Mathematica 5.0 programi (download)

Newtonov fraktalni skup "kriterij konvergencije"
Newtonov fraktalni skup "kriterij iteracije"
Matematički model magnetskih analogija

1. Priroda iteracijske metode
2. Cayleyjev problem
3. Koraci algoritma
4. Primjeri fraktalnih bazena
5. Magnetske analogije fraktalnih bazena
6. Optičke analogije fraktalnih bazena
Literatura
Mathematica 5.0 programi (download)