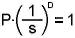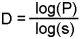Eksperimentalno određivanje fraktalne dimenzije
Hrvoje Eklić
Sadržaj:
1. Uvod: Što su to fraktali?
2. Dimenzije
2.1. Euklidska dimenzija
2.2. Fraktalna dimenzija
3. Eksperimentalno određivanje fraktalne dimenzije linije
3.1. Opis rada programa
3.2. Određivanje fraktalne
dimenzije Kochove krivulje pomoću programa
3.3. Određivanje fraktalne
dimenzije obale
4. Izvršna datoteka programa
5. Literatura
1. Uvod
U sklopu kolegija "Uvod u matematičku teoriju kaosa za inženjere", koji
na Fakultetu elektrotehnike i računarstva u Zagrebu predaje
prof.dr.sc. Mervan Pašić, studenti se upoznaju s pojmom
fraktalne dimenzije i s metodama njezinog računanja na primjerima
klasičnih fraktala. U ovom radu prikazat ćemo vlastiti program
za eksperimentalno određivanje fraktalne dimenzije klasičnih
fraktala kao i skupova fraktalnog tipa koji se pojavljuju u prirodi.
Pomoću programa moguće je na interaktivan način odrediti
fraktalnu dimenziju svih poznatijih fraktala, ali moguće je odrediti i
aproksimaciju fraktalne dimenzije nekog otoka, dijela obale ili bilo koje
slične razlomljene linije.
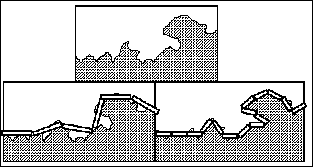
Tipičan primjer fraktala u prirodi izgled je bilo koje obale. Kad joj
dužinu mjerimo npr. štapovima različitih dužina, dobit ćemo
različite rezultate. Štapom najveće dužine izmjerit ćemo
najmanju dužinu te obale. Kraćim štapom izmjerit ćemo veću
dužinu obale jer ćemo mjerenjem uzeti u obzir i manje krivudavosti obalne
linije (Slika 1). Vrlo kratkim štapom izmjerit ćemo dužinu obale koja
može biti vrlo velika.
To je tzv. paradoks dužine obale. Njega najbolje ilustrira
sljedeći podatak: navodeći duljinu zajedničke granice između
Španjolske i Portugala, španjolska enciklopedija navodi podatak od 987 km,
a portugalska enciklopedija navodi 1214 km! Razlika je preko 200 km!
|
|
Slika 1:
Mjerenje dužine obale štapovima različitih dužina
|
Pretpostavlja se da je i cijeli svemir fraktalne prirode. Kao što su zvijezde organizirane u
galaksije na principu gravitacije, tako su i galaksije organizirane u grupe,
grupe u jata i superjata, a superjata u tzv. LSS (large-scale structure).
Međutim, vrlo je
upitno kolika je fraktalna dimenzija LSS-a.
Postoji još mnogo primjera fraktala u prirodi koja nas okružuje. Sve su to oblici kao
što su: planine, stabla, oblaci, jezera i još mnogi drugi.
Otac fraktala je francuski matematičar
Benoit Mandelbrot.
Rođen je 20.11.1924. u Varšavi.
Početkom 70-ih godina prošlog stoljeća opisao je matematiku koja nam danas pomaže
pri analizi nepravilnosti u svijetu. Nove objekte nazvao je fraktali.
Taj naziv dolazi od latinske riječi fractus, što znači razlomljen,
slomljen, polomljen. Mandelbrot je dao i preciznu definiciju
fraktala:
"Fraktali su skupovi točaka kojima je fraktalna
dimenzija veća nego topološka dimenzija".
O fraktalnoj dimenziji bit će više
riječi u sljedećem poglavlju. Osim te definicije, može se reći da su fraktali
skupovi točaka koji imaju 3 važna svojstva: sličnost samome sebi (engl.
self-similarity), fraktalnu dimenziju (engl. fractal dimension) i oblikovanje
iteracijom (engl. formation by iteration).
Sličnost samome sebi svojstvo je objekta da sliči sam
sebi bez obzira koji njegov dio
promatrali i koliko ga puta uvećali. Uvijek ćemo dobiti sliku koja sliči
početnoj.
Fraktalna dimenzija naziva se još i
razlomljena dimenzija zato što ne mora biti cijeli broj, kao što je to npr.
euklidska dimenzija. Ona opisuje i neka svojstva objekta kao što su izlomljenost i hrapavost. Specifično
za fraktalnu dimenziju je to što ona ostaje konstantna bez obzira na mjerilo.
Detaljnije objašnjenje fraktalne dimenzije nalazi se u sljedećem poglavlju.
Oblikovanje iteracijom svojstvo je da se objekt može
generirati nekim računskim ili geometrijskim postupkom koji se uzastopno
ponavlja. Uglavnom, postoji početni objekt (engl. initiator) u koji se
iterativno ugrađuju svojstva generatora (engl. generator).
2. Dimenzije
2.1. Euklidska dimenzija
Likovi klasične, euklidske geometrije su točka, pravac, ploha i tijelo.
Točka ima dimenziju 0 jer nema nijedan stupanj slobode, tj. nema ni dužinu ni
širinu ni visinu.
Pravac ima dimenziju 1 jer ima 1 stupanj slobode.
Ploha ima 2 stupnja slobode, dužinu i širinu, a nema visinu. Dakle, dimenzija plohe
je 2.
Tijelo ima 3 stupnja slobode u euklidskom prostoru: širinu, dužinu
i visinu, dakle dimenzija mu je 3.
Kako matematički odrediti dimenziju?
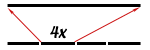
Uzmimo segment (jednodimenzionalni objekt) bilo koje duljine i podijelimo ga na 4
manja segmenta jednakih duljina:
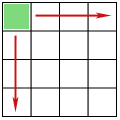
Uzmimo sada neki dvodimenzionalni objekt, npr. kvadrat i podijelimo ga na 16 manjih
jednakih kvadrata:
I na kraju, uzmimo trodimenzionalni objekt, npr. kocku, i podijelimo je na 64 manje
jednake kocke:
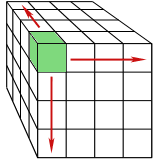
Označimo sa s omjer duže i kraće stranice. U sva 3 primjera s je
jednak 4 jer je kraći segment, odnosno kraća stranica
kvadrata ili kocke, 4 puta kraća od dužeg segmenta,
odnosno duže stranice kvadrata ili kocke.
Označimo s P broj manjih elemenata (segmenata, pravokutnika ili kocaka).
Broj P za prvi primjer (segment) je 4 jer smo početni segment podijelili
na 4 kraća segmenta. Za drugi primjer (kvadrat) P je 16, a za treći primjer
(kocku) P je 64. Možemo uočiti da općenito za P,
s i dimenziju objekta D vrijedi:
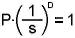
Odavde se dobije:
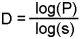
Ta nam formula za sve prethodne primjere daje dobre rezultate.
Za liniju: D = ln(4) / ln(4) = 1,
za kvadrat: D = ln(16) / ln(4) = 2,
za kocku: D = ln(64) / ln(4) = 3.
Zaključak
Neke stvari u svijetu oko nas možemo dobro definirati pomoću 3 dimenzije
klasičnog euklidskog prostora. Na Slici 2 prikazani su neki takvi
primjeri: vlak koji se kreće po tračnicama ima samo jedan stupanj
slobode, kreće se u jednoj dimenziji. Jedrilica koja plovi površinom
jezera kreće se u dvodimenzionalnom prostoru. Jedino zrakoplov ima sva 3
stupnja slobode, tj. može se kretati u bilo kojem smjeru unutar
trodimenzionalnog prostora.

|

|
|
Slika 2:
Primjeri dimenzija i stupnjeva slobode u svijetu oko nas
|
Pogledajmo sljedeći primjer (Slika 3): koliko dimenzija ima ravna aluminijska
folija? Odgovor je jednostavan: aluminijska folija je ploha i ima 2
dimenzije. Međutim, što ako zgužvamo tu aluminijsku foliju i napravimo od
nje kuglu? Koliko sada dimenzija ima ta aluminijska folija? 2? 3? Ili možda
nešto između?

|

|
|
Slika 3:
Problem dimenzije aluminijske folije
|
Osim navedenog problema postoji još mnogo sličnih. Koliko dimenzija ima spužva
koja jest tijelo, ali je iznutra šupljikava pa ne popunjava cijeli svoj
volumen? Koje je dimenzije izlomljena linija koja je u nekom koraku iterativnog
postupka dio nekog fraktala? Koja je dimenzija nekog dijela obale? Odgovori na
ta i mnoga slična pitanja ne leže u klasičnom euklidskom prostoru.
Dimenzije takvih objekata nisu cijeli brojevi. Stoga im
moramo izračunati fraktalnu dimenziju.
2.2. Fraktalna dimenzija
Kao što je već prije napomenuto, fraktalna se dimenzija
naziva još i razlomljenom dimenzijom jer ne mora nužno biti cijeli
broj. Ona opisuje neka svojstva predmeta kao što su izlomljenost,
hrapavost i slično. Fraktalna dimenzija (tj. stupanj nepravilnosti) ostaje
konstantna bez obzira na mjerilo, što se u prirodi vrlo često pokazuje
točnim (tipičan primjer su obalne crte nekog otoka koje imaju
fraktalna obilježja). Fraktalnu dimenziju sebi sličnog skupa definiramo s:
d = log(P) / log(s),
gdje se objekt (skup) sastoji od P kopija samog sebe umanjenih za faktor s.
Ova definicija vrijedi samo za sebi slične skupove. Za širu klasu skupova mogu
se upotrijebiti Hausdorffova i "kutijna" dimenzija (box dimension).
Primjeri izračunavanja fraktalnih dimenzija
1. Cantorova prašina


Georg Ferdinand Ludwig Philipp Cantor rođen je 3.3.1845. u Petrogradu u Rusiji, a umro je 6.1.1918. u Njemačkoj. Cantorova
prašina jedan je od najpoznatijih fraktala.
Nastaje tako što se najprije početnom zatvorenom segmentu
(initiatoru) ukloni srednja trećina (kao otvoreni interval). Rezultat toga su 2 segmenta
od kojih svaki ima dužinu jednaku 1/3 dužine početnog
segmenta. Prethodno opisani korak ponavlja se na novonastalim
segmentima. U sljedećem koraku dobit ćemo 4 segmenta od kojih
je svaki 3 puta kraći od segmenata u prošlom koraku, odnosno 9 puta
kraći od početnog segmenta. Taj se postupak ponavlja do
beskonačnosti. Dakle, Cantorova prašina može se dobiti iterativnim
postupkom. To je jedan od tri osnovna preduvjeta da bi neki objekt
bio fraktal. Sljedeći preduvjet koji objekt mora zadovoljavati je
sličnost samome sebi. To je ovdje osigurano: ako dio Cantorova skupa unutar
intervala [0, 1/3] povećamo 3 puta dobivamo cijeli Cantorov skup. Zadnje od tri
svojstva fraktala je fraktalna dimenzija. Da bismo odredili fraktalnu dimenziju
Cantorove prašine, prema ranije navedenoj formuli d = log(P) / log(s) moramo
odrediti parametre P i s.
Broj P je broj kopija početnog segmenta od kojih je
svaka kopija umanjena s puta. Ako promatramo segmente u nekom n-tom
koraku iterativnog postupka, tada je svaki segment 3 puta manji od onih u
prethodnom (n-1)-om koraku iterativnog postupka. Npr. duljina segmenata u prvom
koraku 3 puta je manja od duljine segmenta u nultom koraku, duljina segmenata u drugom
koraku 3 puta je manja od duljine segmenata u prvom koraku, itd. Dakle, parametar s
jednak je 3. Svaki od segmenata se u svakom sljedećem koraku dijeli na 2
manja segmenta, što znači da je parametar P jednak 2. Dimenzija, dakle,
iznosi:
d = log(P) / log(s) = log(2) / log(3) = 0.6309... .
Dobivena dimenzija zadovoljava i Mandelbrotovu definiciju fraktala, a to je da su
fraktali geometrijske strukture kojima je fraktalna dimenzija veća nego
topološka dimenzija. Topološka dimenzija Cantorove prašine jednaka je
nuli. Fraktalna dimenzija Cantorove prašine približno iznosi 0.6309, što je veće od 0,
dakle, Cantorova prašina je fraktal.
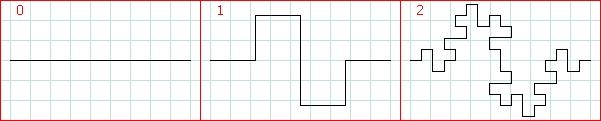
2. Kochova krivulja

Niels Fabian Helge von Koch rođen je 25.1.1870. u Stockholmu, a umro je 11.3.1924., također
u Stockholmu. Poznat je po krivulji koja nastaje tako što se umjesto srednje trećine
početnog segmenta konstruira jednakostraničan trokut bez donje stranice.
Ta je krivulja po njemu i dobila ime. Dužina svake
stranice trokuta upravo je jednaka 1/3 dužine početnog segmenta, a kako je
trokut jednakostraničan, kutovi među svim stranicama
trokuta iznose 60 stupnjeva. Da bismo dobili sliku koja je prikazana u
drugom koraku, opisani postupak treba ponoviti sa svakim segmentom iz prvog
koraka. I tako dalje u beskonačnost.Osobitost Kochove krivulje je što joj je duljina beskonačna, a
sam skup je omeđen. Svaka linija iz neke n-te iteracije
u sljedećoj, (n+1)-oj, iteraciji kopira se u 4 linije (P = 4), od kojih
je svaka linija 3 puta manja od one početne (s = 3). Uvrštavanjem u
formulu za dimenziju dobivamo:
d = log(P) / log(s) = log(4) / log (3) = 1.2618595... .
Fraktalna dimenzija Kochove krivulje je, kao i kod Cantorove prašine, veća od
topološke dimenzije. Topološka dimenzija Kochove krivulje je 1, a fraktalna dimenzija joj je veća od 1.
3. Sierpinskijev trokut

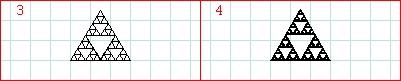
Waclaw Sierpinski rođen je 14.3.1882. u Varšavi, a umro je 21.10.1969., također u Varšavi.
Sierpinskijev trokut nastaje tako što se početnom jednakostraničnom trokutu upiše
jedan manji jednakostranični trokut koji će početni trokut
podijeliti na 4 jednakostranična trokuta. Srednji trokut (jedini kojemu
treći vrh "gleda" prema dolje) se izbaci, a s preostala 3 trokuta
nastavlja se iterativni postupak. Svakom od ta 3 manja trokuta ponovno se upisuje
jednakostranični trokut koji svaki od njih dijeli na 4 nova trokuta i ponovno
se iz svakog izbacuje srednji trokut. Dakle, u svakom koraku iterativnog
postupka od jednakostraničnog trokuta odbacujemo njegov središnji,
također jednakostranični, trokut. U nekom (n+1)-om koraku
dužina stranice trokuta 2 puta je manja nego u n-tom koraku, a svaki od trokuta
kopira se u 3 svoje manje kopije. Dakle, s = 2, a P = 3.
d = log(P) / log(s) = log(3) / log(2) = 1.585... .
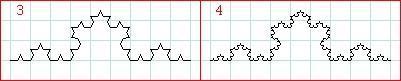
4. Minkowskijev fraktal
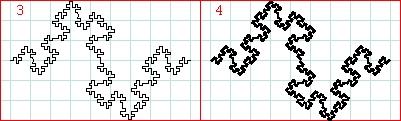
Hermann Minkowski rođen je 22.6.1864., a umro je 12.1.1909. Postupak konstrukcije Minkowskijeva fraktala i proračuna njegove fraktalne dimenzije
vrlo je sličan postupku kod Kochove krivulje. Razlika je u generatoru,
odnosno u motivu svojstva kojeg se u svakom koraku ugrađuju u
početni objekt, tj. u liniju. Izgled generatora vidljiv je na slici u
koraku broj 1 jer je u tom koraku u početnu liniju (korak 0) svojstvo
generatora ugrađeno tek jedanput. U svaku novonastalu liniju ponovno se
ugrađuju svojstva generatora i tako nastaju korak 2, 3, 4, itd.
U nekom (n+1)-om koraku linije su 4 puta manje nego u n-tom
koraku, a svaka linija iz n-tog koraka kopira se u 8 manjih linija u
(n+1)-om koraku. Dakle, s = 4, a P = 8. Dimenzija je:
d = log(P) / log(s) = log(8) / log(4) = 1.5 .
5. Peanova krivulja
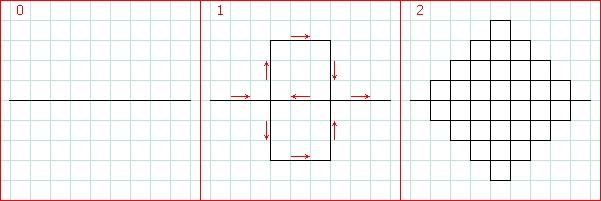
Generator Peanove krivulje, nazvane po
Giuseppeu Peanu,
prikazan je na gornjoj slici u koraku 1. Radi lakšeg
snalaženja označeni su smjerovi svake linije generatora. Nakon što se
od početne linije konstruira generator, koji se sastoji od 9 linija
(P = 9) od kojih je svaka 3 puta manja od početne linije (s = 3),
možemo dobiti drugi korak iterativnog postupka tako što se nad svakom
od 9 linija iz prvog koraka ponovno konstruira generator. Fraktalna dimenzija
iznosi:
d = log(P) / log(s) = log(9) / log(3) = 2 .
Peanova krivulja ima topološku dimenziju 1, a fraktalnu dimenziju 2. To je primjer
krivulje koja jest fraktal jer joj je fraktalna dimenzija veća od
topološke, a fraktalna dimenzija joj je ipak cjelobrojna, a ne razlomak.
To je zato što ova krivulja, kako broj iteracija teži u
beskonačnost, prekriva cijelu površinu.
3. Eksperimentalno određivanje fraktalne dimenzije linije
3.1. Opis rada programa
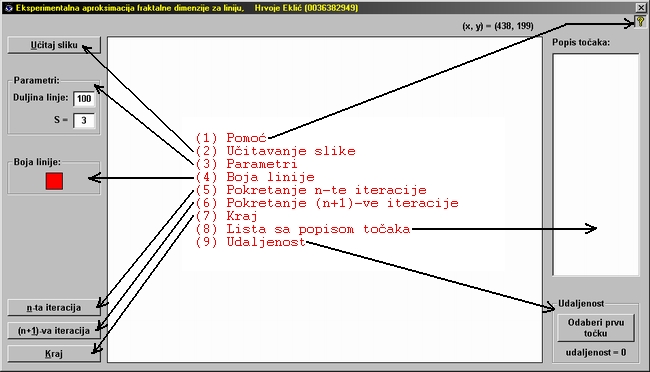
Gornja slika prikazuje izgled prozora programa. Svi bitni dijelovi programa
označeni su brojevima (1) do (9). Za dodatne upute o korištenju
programa kliknite na (1) "Pomoć". U nastavku ćemo objašnjenje rada
programa demonstrirati određivanjem fraktalne dimenzije Kochove
krivulje.
Program za računanje fraktalne dimenzije koristi formulu
d = log(P) / log(S).
S je omjer veće i manje stranice, a P je omjer broja linija
u (n+1)-voj
iteraciji i n-toj iteraciji. U polju s parametrima (3) prije početka
rada s programom potrebno je upisati početnu duljinu linije i S, tj.
omjer veće i manje linije. Na primjer, ako u polju s parametrima
(3) upišemo za dužinu linije 100, a za S upišemo 4, to znači da ćemo
u n-toj iteraciji koristiti liniju dužine 100 piksela, a u (n+1)-oj iteraciji
liniju dužine 25 piksela zato što je S = 4, a 100 / 4 = 25. Dakle, S zadajemo
sami, a P ćemo dobiti nakon što neku liniju ili fraktal prijeđemo prvo
linijom veće dužine, a zatim i linijom manje dužine. Na primjer,
ako u n-toj iteraciji liniju ili fraktal prijeđemo s 3 duže
linije, a u (n+1)-oj iteraciji s 15 linija koje su S puta kraće,
tada P iznosi: P = 15 / 3 = 5.
Za navedeni primjer S iznosi 4, a P iznosi 5. U tom
slučaju fraktalna dimenzija bila bi
d = log(P) / log(S) = log(5) / log(4) = 1.16 .
3.2. Određivanje fraktalne dimenzije Kochove krivulje pomoću programa
Da bismo odredili fraktalnu dimenziju Kochove krivulje pomoću programa,
potrebno je učiniti sljedeće:
1. Učitati sliku Kochove krivulje klikom na gumb za učitavanje slike
(2). Nakon pritiska na gumb u izborniku treba odabrati
sliku (u jpg ili bmp formatu) koju treba učitati. Ta će se
slika prikazati u okviru za sliku u središnjem dijelu prozora
programa. Ovaj korak nije nužan, ali će olakšati daljnji rad s
programom. Kochova krivulja relativno je jednostavna, ali za neke
složenije linije (npr. linije neke obale ili otoka) gotovo da je
nemoguće odrediti fraktalnu dimenziju bez slike te linije. Nakon
učitavanja slike prozor programa izgleda kao na slici dolje.
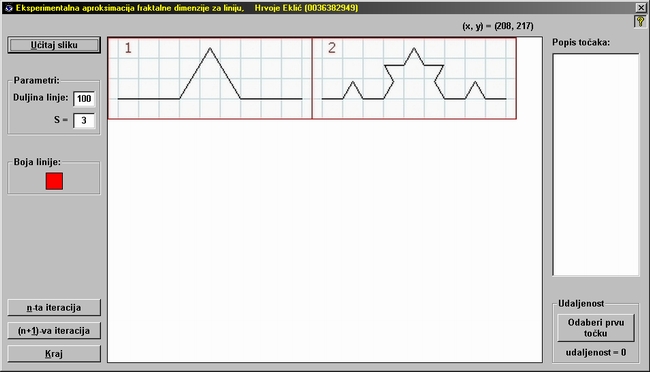
2. Da bismo odredili fraktalnu dimenziju nekog fraktala, potrebno je uzeti 2 susjedne
iteracije: n-tu i (n+1)-u. U konkretnom slučaju, slika koju smo
učitali prikazuje Kochovu krivulju u 1. i 2. koraku iterativnog postupka.
Međutim, isto tako mogli smo odabrati i 0. i 1. korak iteracije, ili 5. i
6., samo je važno da su to 2 susjedna koraka iterativnog postupka. Sada
treba odrediti početnu
dužinu linije. Za početnu dužinu linije treba uzeti dužinu jedne linije s
gornje slike koja prikazuje Kochovu krivulju u 1. koraku iterativnog postupka.
Da bismo odredili koliko ta dužina iznosi, potrebno je kliknuti na gumb u okviru
(9) "Udaljenost": "Odaberi prvu točku". Nakon toga treba kliknuti mišem na
početak linije kojoj želimo saznati dužinu. Sada pomaknemo kursor mišem do
kraja te linije, a u okviru (9) "Udaljenost" na dnu okvira pisat će koliko
ta dužina iznosi piksela. Taj broj upišemo u okvir (3) "Parametri", u polje
"Duljina linije". Da bismo odredili S, tj. omjer dužina duže i kraće
linije, isti postupak mjerenja dužine možemo ponoviti i za jednu kraću
liniju, tj. za bilo koju liniju prikazanu na gornjoj slici iz 2. koraka
iterativnog postupka. Sada, kada znamo dužinu i duže i kraće linije, u
okvir (3) "Parametri" u polje S upišemo koliko iznosi omjer dužina duže i
kraće linije. Međutim, kako se radi o Kochovoj krivulji, poznato je
da je omjer dužina duže i kraće stranice jednak 3. Osim toga, omjer dužina
vidljiv je i sa slike. U ovom slučaju mjerenje ne moramo provoditi i na
dužoj i na kraćoj liniji, već je dosta izmjeriti dužinu duže linije,
a S npr. odrediti sa slike.
3. Nakon učitavanja slike i određivanja početne dužine linije i
parametra S, treba kliknuti na gumb (5) "n-ta iteracija". Tada cijeli fraktal u
n-tom koraku iterativnog postupka
(u konkretnom slučaju je n = 1)
treba prijeći linijama. Početna dužina linije zadana je u
okviru (3) "Parametri". Krenimo npr. slijeva nadesno. Kliknimo mišem na krajnje
lijevu točku krajnje lijeve linije. Nakon toga kliknimo mišem na desnu
točku te iste linije. Nakon toga na sljedeću točku u nizu i
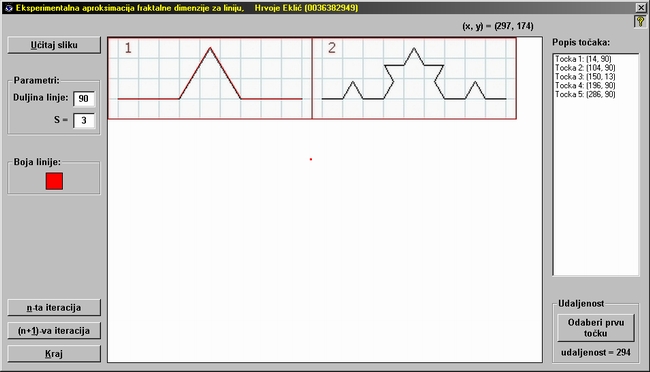
tako dalje dok ne dođemo do zadnje točke zadnje linije fraktala. U
svakom trenutku program se brine da su sve linije koje ste povukli jednake
dužine, i to upravo one početne zadane dužine linije. Popis svih
točaka na koje ste kliknuli nalazi se na desnoj strani prozora programa, a
označen je brojem (8). Nakon što ste cijeli fraktal prešli linijama prozor
programa izgledat će slično kao slika dolje (sve linije koje
prikazuju fraktal u 1. koraku iteracije bit će prekrivene crvenim
linijama, a u popisu točaka (8) nalazit će se popis svih točaka
na koje ste kliknuli).
U zadnjem koraku preostaje napraviti isto što i u prethodnom, ali sa S puta
manjom dužinom linije i ovoga puta ne na n-tom, nego na (n+1)-om koraku
iterativnog postupka. Prvo treba kliknuti na gumb (6) "(n+1)-a iteracija". Tada
program dužinu linije kojom trebate prijeći cijeli fraktal ili liniju
automatski smanjuje S puta. Nakon toga kliknite na prvu točku prve linije
fraktala (bilo s lijeve, bilo s desne strane) u (n+1)-om koraku
iteracije. U ovom konkretnom slučaju, budući da je
n = 1, n+1 = 2. A slika Kochove krivulje u 2. koraku
iterativnog postupka upravo je prikazana na
desnoj polovici slike koju smo učitali. Nakon što linijama prekrijemo i
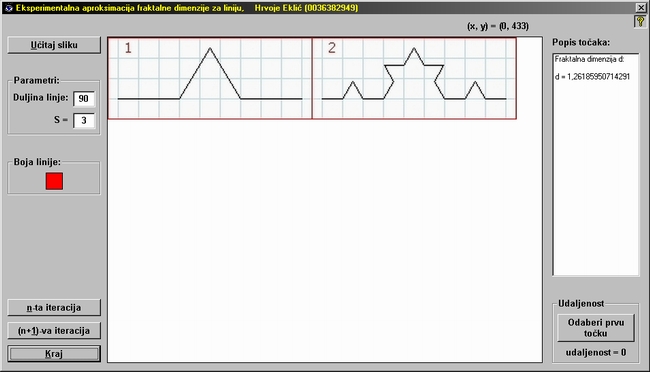
cijelu Kochovu krivulju u 2. koraku iterativnog postupka, preostaje nam još samo
mišem kliknuti na gumb (7) "Kraj". Tada će se u listi (8) s desne strane
prozora programa ispisati rezultat: d = 1,2618595..., što je upravo
očekivani rezultat jer smo u prethodnom proračunu za Kochovu krivulju
izračunali da joj je fraktalna dimenzija jednaka 1.2618595. Ispisani
rezultat prikazan je na donjoj slici.
3.3. Određivanje fraktalne dimenzije obale
Učitajmo sliku nekog dijela obale ili otoka kojemu želimo izračunati
fraktalnu dimenziju. Prozor programa prikazan je na slici dolje.
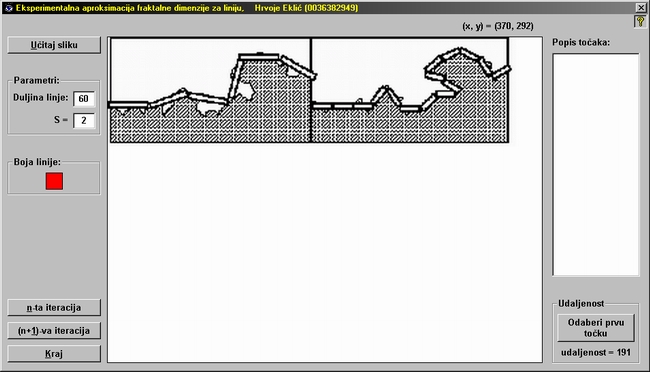
2. Potrebno je odrediti parametre "Duljina linije" i "S". Duljina linije je
početna dužina, tj. dužina dužeg "štapa" kojim ćemo prvo mjeriti
dužinu obale. To je dužina "štapa" prikazanog na lijevoj polovici
učitane slike. Pomoću alata za mjerenje udaljenosti u donjem desnom
kutu prozora programa odredimo udaljenost od početka do kraja
tog "štapa". Dužina "štapa" u ovom primjeru iznosi 60 piksela pa to upišemo
u okvir s parametrima na lijevoj strani prozora programa. Nakon toga na isti
način izmjerimo i dužinu kraćeg "štapa" prikazanog na desnoj polovici
učitane slike. Ta dužina iznosi 30 piksela, što je dva puta kraće od
dužine dužeg "štapa", pa je omjer dužina dužeg i kraćeg "štapa" S = 2.
Vrijednost 2 upisujemo u odgovarajuće polje okvira s parametrima.
3. i 4.
Sada kliknemo na gumb "n-ta iteracija" i
prijeđemo cijelu sliku obale dužim "štapom" tako da krenemo od jedne
strane obale (lijeve ili desne) i mišem slažemo linije preko
linija obale tako dugo dok ne dođemo do druge strane obale. Nakon
toga kliknemo na gumb "(n+1)-a iteracija" i ponovimo cijeli postupak
sa S puta kraćom linijom. U konkretnom slučaju, prvo liniju obale
prijeđemo linijama dužine 60 piksela, a nakon toga linijama dužine 30
piksela jer je S = 2. Kao što se vidi na gornjoj slici, da bismo obalu prekrili
dužim štapovima, potrebno je 6 štapova, a da bismo obalu prekrili
kraćim štapovima, potrebno je 15 štapova. Na kraju kliknemo na gumb "Kraj"
i u listi na desnoj strani prozora pojavit će se rezultat: d = 1.3219...
To je fraktalna dimenzija promatranog dijela obale. Što je fraktalna dimenzija
nekog dijela obale veća, to je taj dio obale više krivudav, tj.
"razvedeniji".
4. Izvršna datoteka programa
Izvršnu datoteku programa možete isprobati ovdje.
Napomena:
Program je napisan za Microsoft Windows XP u programskom jeziku Visual Basic
6.0, te je potrebno imati instalirane Visual Basic Runtime kontrole. Njih je
moguće pronaći na CD-u u svim odgovarajućim informatičkim
časopisima ili
ovdje.
5. Literatura
[1] Mervan Pašić: Nastavni materijal kolegija "Uvod u
matematičku teoriju kaosa za inženjere", FER, Zagreb.
[2] H.O.Peitigen, H.Jurgens, D.Saupe:
Chaos and Fractals. New Frontiers of Science, Springer,
Berlin, 1992.
[3] Vlatka Antončić, Andro Galinović:
Galerija fraktala,
Hrvatski matematički elektronski časopis "math.e", br. 2, 2004.
[4]
Fractals and the Fractal Dimension, Vanderbilt University.
[5] C. Lanius:
Fractal Dimension, Rice University.
[6] M.A. Connors:
Exploring Fractals, University of Massachusetts, Amherst.
1. Uvod: Što su to fraktali?
2. Dimenzije
2.1. Euklidska dimenzija
2.2. Fraktalna dimenzija
3. Eksperimentalno određivanje fraktalne dimenzije linije
3.1. Opis rada programa
3.2. Određivanje fraktalne
dimenzije Kochove krivulje pomoću programa
3.3. Određivanje fraktalne
dimenzije obale
4. Izvršna datoteka programa
5. Literatura