
Broj 3













Branka Srdić
Kako su računali stari Egipćani?

Jedna od najranijih kultura i civilizacija što ih je čovjek stvorio na Zemlji bila je staroegipatska. I danas ćemo se još uvijek ponovno i ponovno zadiviti pred ostacima te velike baštine, razasutim po muzejima svijeta i u svojoj postojbini: bilo da je riječ o umjetničkim djelima u muzeju u Kairu, npr. iz zbirke nađene u Tutankamonovoj grobnici, bilo da motrimo ostatke čudesne građevine kraljice Hatšepsut, njezina hrama u Der el Bahariju, ili velikih piramida, hrama u Luksoru ili grobnica u Dolini kraljeva, bilo da čitamo šifrirane tekstove iz staroegipatske Knjige mrtvih, bilo da iz sačuvanih skica i opisa pokušamo rekonstruirati kako su podizane njihove monumentalne građevine… U svakom ćemo slučaju ostati iznenađeni pred snagom duha i volje i pred dubinom misli što su nikle i razvile se u dolini Nila prije nekoliko tisućljeća.

|
I staroegipatska je matematika jedna od najranijih epoha razvoja te znanosti. Posebno jedna od prvih grana matematike, geometrija, već samim svojim nazivom otkriva i svoje podrijetlo. To je po postanku grčka riječ koja bi, doslovno prevedena, značila "mjerenje zemlje". A upravo kao mjerenje zemlje geometrija se široko razvila već u starom Egiptu. Poslovična izreka, "Egipat je dar Nila", dovoljno je poznata. Bez blatnjavih žutih voda te rijeke što su tisućljećima natapale zemlju, ne bi se razvila tako bogata civilizacija starog Egipta. No poslije redovnih velikih poplava Nila, svake bi se godine granice zemljišnih posjeda izbrisale i trebalo ih je ponovno odrediti – valjalo je, dakle, premjeravati zemljišta. Izgradnja veličanstvenih hramova, piramida, kipova, također je zahtijevala određena znanja iz geometrije. |

 O staroegipatskoj matematici doznajemo ponajviše iz dvaju glasovitih
papirusa: Ahmesovog ili Rhindovog (desno) i Moskovskog (lijevo).
Rhindov papirus je 1858. otkrio škotski egiptolog Henry Rhind u Luxoru. To je zapravo
svitak duljine 6 m, širine 30 cm. Pisao ga je pisar Ahmes oko 1650 g. pr. Kr. i
vjerojatno je nastao tako što je Ahmes
prepisivao neki spis star 200 godina.
Danas se čuva u British Museumu u Londonu, a sadrži 87 matematičkih
problema. To je jedna kompletna "studija o svim stvarima,
pogled u unutrašnjost
svega što postoji, saznanje o tamnim tajnama", kako piše u samom papirusu. Ahmesov
papirus je zbirka tablica i vježbi, retorička u svojoj formi, koja je
namijenjena uglavnom učenju matematike. Sadrži vježbe iz aritmetike,
algebre, geometrije i raznih mjerenja. Moskovski
papirus otkrio je 1893. godine V. S. Golenichev. Dug je 6 m, širok 8 cm.
Sadrži 25 problema, od kojih mnogi nisu čitljivi. Čuva se
u Moskovskom muzeju.
O staroegipatskoj matematici doznajemo ponajviše iz dvaju glasovitih
papirusa: Ahmesovog ili Rhindovog (desno) i Moskovskog (lijevo).
Rhindov papirus je 1858. otkrio škotski egiptolog Henry Rhind u Luxoru. To je zapravo
svitak duljine 6 m, širine 30 cm. Pisao ga je pisar Ahmes oko 1650 g. pr. Kr. i
vjerojatno je nastao tako što je Ahmes
prepisivao neki spis star 200 godina.
Danas se čuva u British Museumu u Londonu, a sadrži 87 matematičkih
problema. To je jedna kompletna "studija o svim stvarima,
pogled u unutrašnjost
svega što postoji, saznanje o tamnim tajnama", kako piše u samom papirusu. Ahmesov
papirus je zbirka tablica i vježbi, retorička u svojoj formi, koja je
namijenjena uglavnom učenju matematike. Sadrži vježbe iz aritmetike,
algebre, geometrije i raznih mjerenja. Moskovski
papirus otkrio je 1893. godine V. S. Golenichev. Dug je 6 m, širok 8 cm.
Sadrži 25 problema, od kojih mnogi nisu čitljivi. Čuva se
u Moskovskom muzeju.
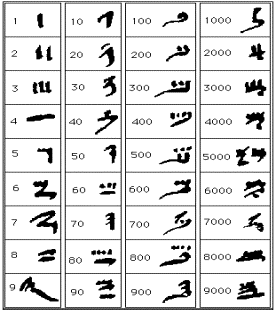
Stari Egipćani imali su razvijeni decimalni
sustav i svoje oznake za brojeve:
|
|
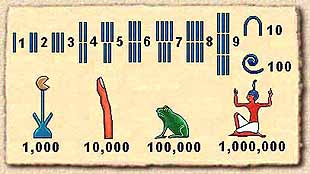
| hijeratski znaci | hijeroglifski znaci |
Hijeroglifskim znacima se pisalo po kamenu kako s lijeva na desno,
tako i obrnuto, a ponkad i odozgor prema dolje.
Različito pisanje ne stvara probleme kod čitanja bojeva
jer egipatski način pisanja brojeva nije pozicijski.
Hijeratički su znaci uvedeni za brzo pisanje po papirusu, drvu ili po lončariji.
Osim navedenih, upotrebljavali su se povremeno i neki posebni znakovi za brojeve koji nisu dekadske jedinice. Npr. za broj dva crtali bi se goveđi rogovi, za broj pet morska zvijezda, a ljudska glava bila je i oznaka za broj sedam (7 otvora).
Na poseban su način označavali razlomke, tako specifičan da nema sličnosti ni s jednom drugom kulturom. Razlomak s brojnikom jedan zapisivao se tako da se iznad znaka za nazivnik stavio poseban znak sa značenjem "dio". Svi razlomci pisali su se s jediničnim brojnikom, a ako to nije bilo moguće, onda su ga prikazivali kao zbroj takvih.
Evo nekoliko
primjera zapisa nekih brojeva:
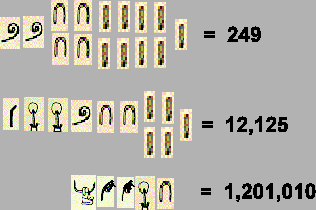

Koristili su brojevni sustav s bazom 10, a jedna od glavnih razlika između hijeratičkih brojeva i našeg brojevnog sustava jest da hijeratički brojevi nisu bili pisani u sustavu mjesnih vrijednosti, tako da su znamenke mogle biti pisane bilo kojim redoslijedom. Hijeratički je sustav adicijski sustav. Vidimo da se, recimo, broj 249 zapisuje kao 249 = 2
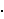 100 +
4
100 +
4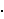 10 + 9,
pa u zapisu imaju dva znaka za 100, četiri znaka za 10 i devet znakova za 1.
10 + 9,
pa u zapisu imaju dva znaka za 100, četiri znaka za 10 i devet znakova za 1.
Kako su
računali stari Egipćani?
Egipatski
brojevni sustav nije bio pogodan za računanje, ali je trgovina zahtijevala
zbrajanje, oduzimanje, množenje, dijeljenje te rad s razlomcima.
Zbrajati je bilo najlakše!
Zbrajalo se skupljanjem istih simbola zajedno i pretvaranjem njih 10 u jedan simbol sljedeće razine:
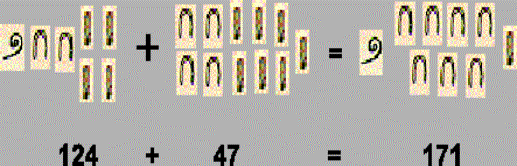
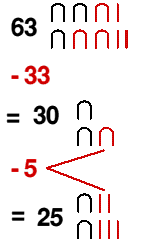 Oduzimalo se tako da se odmicao određeni broj
istih simbola. Ovo je znalo biti i komplicirano kad se moralo oduzeti više
simbola nego što ih je bilo prisutno u prikazu. Npr.,
evo kako bi izračunali 63-38.
Oduzimalo se tako da se odmicao određeni broj
istih simbola. Ovo je znalo biti i komplicirano kad se moralo oduzeti više
simbola nego što ih je bilo prisutno u prikazu. Npr.,
evo kako bi izračunali 63-38.
Od 6 desetica možemo oduzeti 3 desetice, ali možemo ukloniti samo 3 jedinice. Još nam preostaje 5 jedinica za oduzimanje. Jedna od preostalih desetica potrebna je da se omogući oduzimanje sljedećih 5 jedinica jer
1 desetica – 5 jedinica = 10 jedinica – 5 jedinica = 5 jedinica.
Točan mehanizam oduzimanja koji su koristili nije sasvim jasan, iako ova ilustracija pokazuje kojim je redoslijedom pisar mogao provesti oduzimanje.
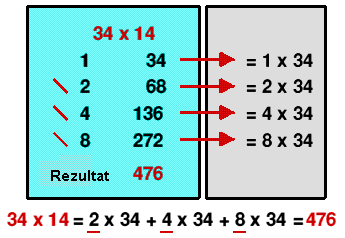
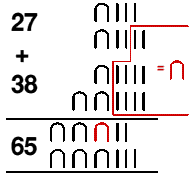
Množenje prirodnih brojeva odaje nam da su se služili i potencijama broja 2. Stari Egipćani množili su dva broja koristeći udvostručavanje brojeva.
U plavom pravokutniku prikazan je njihov zapis, a sivi pravokutnik i račun ispod pravokutnika objašnjava metodu.
Broj su udvostručavali zbrajajući ga samog sa sobom, dakle samo su zapisali brojeve jedan ispod drugoga i pretvorili svakih 10 istih simbola u simbol sljedeće razine.
Kako nisu imali razvijen pozicijski zapis brojeva, moramo starim Egipćanima priznati veliku spretnost i ekonomičnost u računanju.
Kao što se vidi u tablici hijeroglifskih znakova,
egipatski brojevni sustav koristio je simbole koji predstavljaju potencije
broja 10 s eksponentima od 0 do 6.
I oni su uočili da je množenje broja s 10
jednostavno: zamijenili bi svaki simbol onim susjednim po veličini, npr.
236 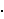 10 = (6 jedinica postaje 6 desetica, 3
desetice postaju 3 stotice, 2 stotice postaju 2 tisućice)
= 2 tisućice, 3 stotice i 6 desetica = 2360.
10 = (6 jedinica postaje 6 desetica, 3
desetice postaju 3 stotice, 2 stotice postaju 2 tisućice)
= 2 tisućice, 3 stotice i 6 desetica = 2360.
Evo jednog od posljednjih problema Rhindova papirusa: "Na imanju je sedam zgrada.
U svakoj od njih je sedam mačaka. Svaka od mačaka uhvati po
sedam miševa, a svaki od njih pojede po sedam zrna pšenice. Svako bi zrno
moglo dati sedam mjerica žita. Koliko je na imanju ukupno zgrada, mačaka,
miševa, zrna pšenice i mjerica žita?"
Rješenje u našim oznakama dano je s:
zgrada 7
mačaka 49
miševa 343
zrna 2401
mjerica 16807
-----------------------
19607
|
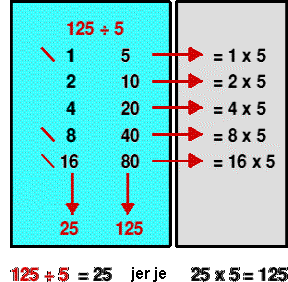
Dijeljenje u starih Egipćana zahtijevalo je korištenje množenja i
vrlo često upotrebu razlomaka. Pogledajmo prvo primjer dijeljenja kad je
rezultat cijeli broj.
Razmišljanje je sljedeće:
a |
|
Kad je pisar morao računati s
razlomcima, bio je suočen s mnogim problemima, uglavnom vezanim za njihovo
zapisivanje. Njihove metode zapisivanja nisu im dopuštale da pišu jednostavne
razlomke kao što su 3/5 ili 15/33 zato što su svi razlomci morali biti
prikazani s brojnikom 1. Ako to nije bilo moguće, onda se razlomak morao
zapisati kao zbroj razlomaka s brojnikom 1. Iznimka u tome je bio razlomak 2/3. Razlomci su
zapisivani tako da je iznad nazivnika stavljen hijeroglif koji je označavao
"otvorena usta"
![]() .
Danas pojednostavljeno razlomke
s jedinicom u brojniku pišemo s kosom crtom iza koje slijedi nazivnik, npr.
1/2 zapisujemo kao /2, 1/4 kao /4, dok se iznimka, 2/3, piše //3.
.
Danas pojednostavljeno razlomke
s jedinicom u brojniku pišemo s kosom crtom iza koje slijedi nazivnik, npr.
1/2 zapisujemo kao /2, 1/4 kao /4, dok se iznimka, 2/3, piše //3.
Postojala su i određena pravila pri
računanju s razlomcima:
- kad se razlomak može prikazati na više načina, koristi se način koji zahtijeva najmanji broj jediničnih razlomaka,
- uvijek se koristi najveći mogući jedinični razlomak, osim ako to nije u kontradikciji s prvim pravilom,
- u prikazu razlomka 2/n ne mogu se koristiti dva ista jedinična razlomka,
- jedinični razlomci pišu se od većeg prema manjem.
- Razlomak 3/4 pisar je mogao zapisati kao /2 /4, ili /3 /4 /6. Uvijek se koristi kraća verzija.
- Razlomak 7/12 mogao se zapisati kao /2 /12, ili /3 /4. Pisar bi koristio /2 /12 jer mora koristiti veći jedinični razlomak, /2 koji je veći od /3.
- Razlomak 9/10 nije se mogao zapisati kao /2 /5 /5 zato što se jedinični razlomak može koristiti samo jednom u prikazu. Zato bi se 9/10 pisao kao //3 /5 /30.
- Prijašnji primjer pokazuje kako su razlomci u zbroju pisani u padajućem redoslijedu: //3 > /5 > /30.
| 1/3 | 3/4 = 1/2 + 1/4 |
|
|
|
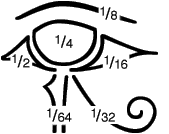 Stari Egipćani
vjerovali su da ih "Rx" simbol, tj. simbol boga Horusa štiti od
zla. Zato su i u
matematiku ugradili simboliku pa su razvili i svojevrstan brojevni
sustav koji se koristio za prepisivanje
lijekova, podjelu zemlje ili sjemenja. Razlomke su tvorili
tako što su kombinirali pojedine dijelove
simbola oka boga Horusa. Svaki dio imao je različitu vrijednost.
Cjelokupni simbol oka ima vrijednost 1, a cijeli
sustav se temelji na podjeli na polovice. Pola od 1
je 1/2, pola od 1/2 je 1/4, itd. sve do 1/64.
Stari Egipćani
vjerovali su da ih "Rx" simbol, tj. simbol boga Horusa štiti od
zla. Zato su i u
matematiku ugradili simboliku pa su razvili i svojevrstan brojevni
sustav koji se koristio za prepisivanje
lijekova, podjelu zemlje ili sjemenja. Razlomke su tvorili
tako što su kombinirali pojedine dijelove
simbola oka boga Horusa. Svaki dio imao je različitu vrijednost.
Cjelokupni simbol oka ima vrijednost 1, a cijeli
sustav se temelji na podjeli na polovice. Pola od 1
je 1/2, pola od 1/2 je 1/4, itd. sve do 1/64.
 Npr., da bismo prikazali razlomak 5/8,
kombiniramo razlomke 1/8 i 1/2.
Npr., da bismo prikazali razlomak 5/8,
kombiniramo razlomke 1/8 i 1/2.
Važnost 2/3 kao jedinog razlomka koji nisu rastavljali na jedinične i koji
su vrlo mnogo koristili u računima, pronalazimo u tome što su stari Egipćani
znali i koristili činjenicu da se 2/3 od 1/n može računati kao
2/3 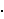 1/n = 1/(2n) +
1/(6n). Kako su bili vješti u računanju, a pogotovo zato što nigdje nisu
pronađeni neki pomoćni računi, skloni smo vjerovanju da su imali dobro i
precizno razrađene tablice rastava razlomaka, zbrajanja i oduzimanja osnovnih i
sl., koje su im omogućavale brzo i efikasno računanje s razlomcima.
1/n = 1/(2n) +
1/(6n). Kako su bili vješti u računanju, a pogotovo zato što nigdje nisu
pronađeni neki pomoćni računi, skloni smo vjerovanju da su imali dobro i
precizno razrađene tablice rastava razlomaka, zbrajanja i oduzimanja osnovnih i
sl., koje su im omogućavale brzo i efikasno računanje s razlomcima.

Promotrimo li fantastične građevine koje su stari Egipćani ostavili u prilog svjetskoj
baštini, ne možemo a da se ne zapitamo koliko su dobro imali razvijenu
geometriju, stereometriju i sve ono što im je bilo potrebno za izgradnju
piramida i hramova. Znamo da su znali računati nagib piramide, volumen krnje
piramide te volumen piramide. Računali su površinu trokuta kao 1/2
umnoška dviju kraćih stranica (što vrijedi samo za pravokutan trokut);
malena odstupanja nisu im značila previše. Znali su izračunati i površinu
pravokutnika kao umnožak duljina njegovih stranica.
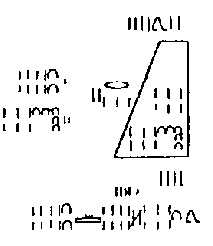
|
dio Moskovskog papirusa o izračunavanju volumena krnje piramide |
Ono što jest fascinantno, a pronađeno je u Ahmesovom papirusu,
je kako su računali površinu
kruga:
- pretpostavimo da krug ima dijametar od 9 kheta (khet je jedinica za duljinu),
- uzmi 1/9 dijametra, dakle 1,
- ostatak je 8,
- pomnoži 8 sa 8,
- dobiješ 64 i to je površina!
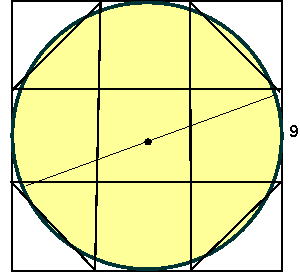 Evo i načina ma koji se može dobiti
formula slična egipatskoj za površinu kruga.
Uspoređujemo krug s kvadratom:
Evo i načina ma koji se može dobiti
formula slična egipatskoj za površinu kruga.
Uspoređujemo krug s kvadratom:
- promjer kruga je 9, dakle, opiši mu kvadrat stranice duljine 9
- podijeli svaku stranicu kvadrata na trećine
- formiraj osmerokut kao na slici
- površina dobivenog osmerokuta približno je jednaka površini kruga
- površina osmerokuta jednaka je površini kvadrata umanjena za dva mala kvadrata sačinjena od 4 "odrezana" trokuta
P(osmerokut) = 9
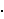 9 – 4(1/2
9 – 4(1/2 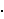 3
3 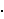 3) = 63
3) = 63
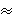 64 = 82
64 = 82
Staroegipatska algebra bila je retorička, problemi i rješenja dani su
riječima. Znali su rješavati jednadžbe prvog stupnja s tim da su obavezno
provodili analizu i sintezu pri rješavanju, tj. svako rješenje su uvrštavali u
početni problem da se uvjere da to uistinu i jest pravo rješenje.
Stari Egipćani nisu poznavali oznake za množenje, dijeljenje, jednakost, drugi korijen, decimalnu točku, nisu čak ni znali za "obični" razlomak p/q, nisu se pitali zašto nešto funkcionira, nisu tražili univerzalnu istinu formuliranu simbolima koji bi jasno i logički pokazali njihov misaoni proces. Ali su se zato koristili i sedmeroznamenkastim brojevima, imali su neku čudnu mješavinu jednostavnosti i začudne kompliciranosti u svojim računima, ali taj se koncept pokazuje kao potpuno jedinstvena i zatvorena cjelina.
Zato se može reći da je egipatska matematika jedini sačuvani čisti primjerak računske tehnike koja je bila vrlo razvijena, koja u čitavom svom razvoju nije doživjela nikakav bitni diskontinuitet, već se u potpunosti temelji na osnovi računanja - na brojenju i pojmu razlomka.
Literatura:
[1] V. Devide, Matematika kroz kulture i epohe, Školska knjiga, Zagreb, 1979.[2] R. J. Gillings, Mathematics in the Time of Pharaohs, Denver Publications Inc., New York, 1982.
[3] Ancient Egyptian mathematics, The MacTutor History of Mathematics archive
http://www-gap.dcs.st-and.ac.uk/~history/Indexes/Egyptians.html
[4] The Mathematics od Ancient Egypt, University of New York at Buffalo
http://www.math.buffalo.edu/mad/Ancient-Africa/mad_ancient_egypt.html
[5] D. E. Joyce, History of Mathematics - Egypt
http://aleph0.clarku.edu/~djoyce/mathhist/egypt.html
[6] M. Millmore, Ancient Egypt - Egyptian Math
http://www.eyelid.co.uk/numbers.htm
[7] V. Beaumont, Ancient Egyptian Mathematics
http://home.clara.net/beaumont/egypt/maths/
[8] Ancient Egypt Teacher Resource File, Internet School Library Media Center
http://falcon.jmu.edu/~ramseyil/egypt.htm