Kosinus-sinus dekompozicija ortogonalnih matrica malog reda
Vjeran Hari i Vida Zadelj-Martić
Sadržaj:
1. Uvod u kosinus-sinus dekompoziciju
2. Singularna dekompozicija matrice reda dva
3. CS dekompozicija ortogonalnih matrica reda 2 i 3
4. CS dekompozicija ortogonalne matrice reda 4
5. Jedna primjena CS dekompozicije
Literatura
1. Uvod u kosinus-sinus dekompoziciju
Realna matrica Q reda n je ortogonalna
ako zadovoljava jedan od uvjeta: QτQ =I
ili QQτ = I, pri čemu je sa Qτ označena transponirana matrica
matrice Q, dok
je I jedinična matrica. Može se pokazati da uvjet QτQ = I povlači QQτ = I,
a vrijedi i obratno, uvjet QQτ = I povlači QτQ = I.
Uvjet QτQ = I zapravo
znači da su stupci matrice Q međusobno ortogonalni i da svi imaju jediničnu
(duljinu) normu. Zato se kaže da su stupci ortogonalne matrice ortonormirani.
Uvjet QQτ = I znači da su retci od Q ortonormirani.
Ortogonalne matrice su vrlo važne u konstrukciji matričnih algoritama jer
imaju još neka važna svojstva. Ako pomnožimo proizvoljnu n × m matricu A
slijeva s ortogonalnom matricom Q, tada stupci matrice QA imaju redom iste
norme kao i stupci matrice A. Čak i više, kutovi između stupaca matrice A
ostaju nepromijenjeni pri prelasku na matricu QA. Ista svojstva invarijantnosti
vrijede i za retke prizvoljne m × n matrice B pri prelasku na matricu BQ.
Konačno, produkt ortogonalnih matrica je opet ortogonalna matrica, inverz
ortogonalne matrice je ortogonalna matrica, a i jedinična matrica je ortogonalna.
Kosinus-sinus dekompozicija (kraće, CS dekompozicija ili CSD) ortogonalne
matrice Q vezana je uz 2 × 2 particije matrice Q,
pri čemu su Q11 i Q22 kvadratne
reda k i n − k, gdje je k
između 1 i n − 1. Za
takvu particiju CS dekompozicija ima sljedeći oblik
gdje je
ovisno o tome je li
k ≥ n − k
ili je k < n − k.
Ako je k = n − k, tada
se u prvom ili drugom obliku matrice Θ u
relaciji (3)
ispušta jedinična matrica.
Pritom su Γ i Σ dijagonalne matrice s nenegativnim dijagonalnim elementima
γi i σi za koje vrijedi
γ1 ≥ γ2 ≥ … ≥ 0 i
γi2 + σi2 = 1
za sve i. Zbog zadnjeg svojstva, dijagonalni elementi
γi poistovjećuju se s kosinusima,
a σi
sa sinusima nekih kutova, pa odatle i naziv kosinus-sinus
dekompozicija ortogonalne matrice. Očito mora vrijediti
0 ≤ σ1 ≤
σ2 ≤ … ≤ 1.
Uočimo također da za dijagonalne
matrice Γ i Σ vrijedi Γ2 + Σ2 = I.
U gornjim relacijama 0 označava nul-matricu
odgovarajućeg tipa. Matrice U11 i V11
(U22 i V22) su ortogonalne reda k (reda
n − k).
Kako bi izlaganje bilo što jednostavnije, mi ćemo u ovom članku izvesti CS
dekompozicije ortogonalnih matrica reda 2, 3 i 4, te pokazati jednu njihovu
primjenu. No, prije toga trebamo razviti "alate" koje ćemo koristiti. Jedan od
najvažnijih alata je singularna dekompozicija koju ćemo uglavnom koristiti za
matrice reda dva.
2. Singularna dekompozicija matrice reda dva
U konstrukciji algoritma za računanje CS dekompozicije ortogonalnih matrica
koristi se jedna od najvažnijih matričnih dekompozicija: singularna dekompozicija
(engl. singular value decomposition ili kraće SVD). Za naše potrebe, bit će
dovoljno znati kako ju izračunati za matrice reda dva.
Neka je A proizvoljna matrica reda dva. Singularna dekompozicija matrice
A je svaki rastav oblika
|
| A = |
|
| |
= U |
|
| |
Vτ = UΞVτ , α1 ≥ α2 ≥ 0 |
, |
| | (4) |
gdje su U i V ortogonalne matrice reda dva. Kako izgledaju ortogonalne matrice
reda dva? To su ili rotacije ili reflektori (zrcaljenja) u ravnini, pa proizvoljna
ortogonalna matrica W reda dva ima jedan od sljedećih dvaju oblika
Pritom je φ ∈ [0 , 2π] kut kojim je određena W. Neka je
proizvoljni vektor. Tada produkt y = Qx ima u slučaju rotacije oblik
| y = |
|
| |
x = ρ |
|
| cos φ cos ψ − sin φ | sin ψ |
| sin φ cos ψ + cos φ | sin ψ |
| |
= ρ |
|
| |
, |
dok u slučaju reflektora postaje
| y = |
|
| |
x = ρ |
|
| cos φ cos ψ + sin φ | sin ψ |
| sin φ cos ψ − cos φ | sin ψ |
| |
= ρ |
|
| |
. |
Uočimo da se vektori x definirani kutem φ/2 ne mijenjaju kad se
množe s reflektorom (oni su u "zrcalu").
Sljedeća slika daje geometrijski prikaz ovih transformacija pomoću točaka
ravnine. Pritom smo vektoru [α β]τ jednoznačno pridružili
točku (α, β) ravnine. Prikazali smo kako se transformiraju vektori
[1 0]τ,
[0 1]τ i
[α β]τ pri
množenju s W. Odabrali smo φ = 60°.
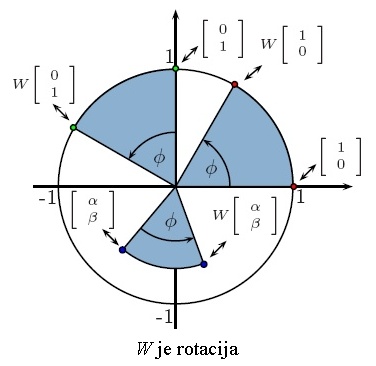
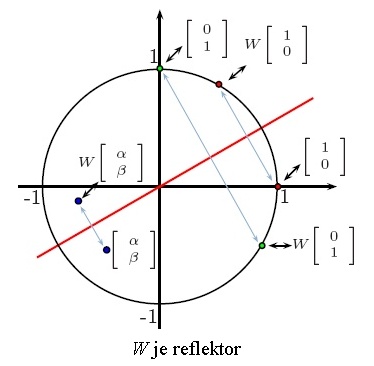
Budući da W ne mijenja normu vektora x, možemo smatrati da je Wx rotirani
vektor x. Pritom, ako je W rotacija,
onda se svaki x rotira za kut φ.
Ako je W reflektor, onda kut rotacije ovisi i o vektoru x (kutu ψ).
Stoga nam singularna dekompozicija daje jednostavnu geometrijsku interpretaciju transformacije
x 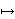 Ax = UΞVτ x:
prvo se x rotira u vektor Vτ x, zatim se
komponente od Vτ x
pomnože nenegativnim brojevima α1 i α2, te se dobije
vektor ΞVτ x. Konačno,
ΞVτ x se rotira matricom U.
Budući da množenje s Vτ i U ne mijenja normu
vektora, norma od Ax ovisi jedino o singularnim vrijednostima matrice A. Isti
zaključak vrijedi i kad je A višeg reda.
Ax = UΞVτ x:
prvo se x rotira u vektor Vτ x, zatim se
komponente od Vτ x
pomnože nenegativnim brojevima α1 i α2, te se dobije
vektor ΞVτ x. Konačno,
ΞVτ x se rotira matricom U.
Budući da množenje s Vτ i U ne mijenja normu
vektora, norma od Ax ovisi jedino o singularnim vrijednostima matrice A. Isti
zaključak vrijedi i kad je A višeg reda.
Jedan algoritam kako izračunati singularnu dekompoziciju
(4), pri čemu su
U i V matrice rotacije, opisan je u
članku [ZA]. Stoga, kad nam zatreba
singularna dekompozicija matrice reda dva, možemo koristiti taj algoritam. Više o
singularnoj dekompoziciji može se naći npr. u poznatoj knjizi [GO].
3. CS dekompozicija ortogonalnih matrica reda 2 i 3
CS dekompozicija ortogonalne matrice Q reda 2, koja je definirana kutem φ,
ima oblik
| Q = |
|
| |
|
|
| |cos φ| | | −|sin φ| |
| |sin φ| | | |cos φ| |
| |
|
|
| |
. |
Bez obzira je li Q rotacija ili reflektor, uvijek je moguće
odabrati predznake u
1. i 3. matrici na desnoj strani gornje jednakosti tako da relacija vrijedi.
Budući da ortogonalna matrica reda jedan ima oblik [1] ili [−1],
desna strana u zadnjoj
relaciji doista predstavlja CSD od Q.
Neka je sada ortogonalna matrica Q reda 3.
Gledajući relacije (1),
(2),
(3),
zaključujemo da CSD za Q ima jedan od oblika,
ili
pri čemu ±1 znači 1 ili -1.
Promotrimo prvi slučaj, kad je Q11 reda dva. Prvo
izračunajmo singularnu dekompoziciju od Q11. Dobijemo
ortogonalne matrice Ũ11 i Ṽ11,
te nenegativne brojeve γ1 i γ2, takve
da vrijedi
| Q11 = Ũ11 |
|
| |
Ṽ11τ, |
γ1 ≥ γ2 ≥ 0 . |
Pomoću Ũ11 i Ṽ11
načinimo ortogonalne matrice
gdje je Q22 = [q33], a
sign(q33) je
predznak od q33 (1 ili -1). Pomnožimo
UτQV
i označimo taj umnožak s X. Ako pokažemo da je
X = Θ, gdje je
Θ oblika kao prva matrica u relaciji
(3),
dokazali smo da je Q =
UΘVτ, CSD matrice Q.
Izračunajmo elemente od X,
| = |
|
| Ũ11τ Q11Ṽ11 | Ũ11τ Q12 |
| sign(q33)Q21 | |q33| |
| |
= |
|
| |
. |
Budući da je X ortogonalna, prva dva stupca, kao i prva dva retka,
moraju biti ortogonalna. To nam daje sljedeće relacije
γ1·0 + 0·γ2 + β1β2 = 0, dakle β1β2 = 0,
γ1·0 + 0·γ2 + α1α2 = 0, dakle α1α2 = 0.
Kad bi bilo γ1 = 0 moralo bi zbog
γ1 ≥ γ2 ≥ 0
biti i γ2 = 0. To, zajedno s
uvjetom β1β2 = 0 povlači da je
ili prvi ili drugi stupac od
X sastavljen od samih
nula. Budući da se to protivi ortogonalnosti matrice
X (svi stupci i svi retci od X su
jedinični), mora biti γ1 > 0. Tvrdimo da mora biti
γ1 = 1. Zaista, kad bi bilo
γ1 < 1, bilo bi zbog
γ2 ≤ γ1,
γ2 < 1.
Kako je |β1| =
√1 − γ12,
|β2| =
√1 − γ22
morali bi β1 i β2 biti različiti od nule,
a to je nemoguće jer je β1β2 = 0.
Time smo pokazali da je
γ1 = 1 i β1 = 0.
Također, budući da je |α1| =
√1 − γ12,
mora biti i α1 = 0. Dakle, ortogonalna
matrica X ima oblik
Stoga je |q33| = γ2 i
α2 = −β2.
Ako je β2 ≥ 0, X = Θ.
Ako je β2 < 0, treba
kao U i V uzeti matrice
Time je dokaz egzistencije CSD vezane za prvu particiju gotov.
Dokaz za drugu particiju matrice Q vrlo je sličan, pa ćemo ga sažeto
prikazati. Prvo izračunamo singularnu dekompoziciju 2×2
podmatrice Q22,
| Q22 = Ũ22 |
|
| |
Ṽ22τ , γ1 ≥ γ2 ≥ 0 , |
a zatim sagradimo matrice U i V kako slijedi
gdje je Q11=[q11].
Matrica X=UτQV sada ima oblik
| X = |
|
| |q11| | α1 | α2 |
| β1 | γ1 | 0 |
| β2 | 0 | γ2 |
| |
, γ1 ≥ γ2 ≥ 0 . |
Istim zaključivanjem, odmah dobijemo
γ1 = 1,
α1 = 0,
β1 = 0,
te |q11| = γ2
i β2 = −α2.
Ako je β2 ≥ 0, U i V
daju X = Θ.
Ako je β2 < 0, moramo U i
V promijeniti, tako da im promijenimo predznake u svim elementima zadnjih
stupaca.
Uočimo da prvi oblik CS rastava ortogonalne matrice Q ima
rotacije u istim
ravninama kao i rotacije vezane uz Eulerove kutove. Stoga je θ
Eulerov kut ako
je q33 ≥ 0,
jer je |q33| =
cos θ ≥ 0 i jer je
q33 kosinus Eulerova kuta. Za ostale
kutove mogla bi se napraviti analiza, jer matrice
U11 i V11
mogu biti i reflektori.
Također, u analizi bi se trebalo pretpostaviti
da je determinanta od Q jednaka 1.
4. CS dekompozicija ortogonalne matrice reda 4
Za ortogonalnu matricu Q reda 4 postoje tri moguće particije koje daju CS
dekompoziciju: kad je Q11 reda 1, 2 i 3.
Započnimo razmatranje s
najzanimljivijim slučajem kad su obje podmatrice Q11 i Q22 reda dva.
4.1 Q11 je reda dva
Izračunajmo singularne dekompozicije podmatrica Q11
i Q22,
Q11 = U11Γ1V11τ,
Q22 = U22Γ2V22τ
i sagradimo ortogonalne matrice
Množenjem lako dobijemo
| Q̃ = UτQV = |
|
| U11τQ11V11 | U11τQ12V22 |
| U22τQ21V11 | U22τQ22V22 |
| |
= |
|
| |
|
| = |
|
| γ1 | 0 | a | b |
| 0 | γ2 | c | d |
| e | f | γ3 | 0 |
| g | h | 0 | γ4 |
| |
, |
γ1 ≥ γ2 ≥ 0,
γ3 ≥ γ4 ≥ 0. |
| | (6) |
Pritom su
γ1 i γ2 singularne vrijednosti od Q11, dok su
γ3 i γ4 singularne
vrijednosti od Q22. Odatle je proizašlo da je
γ1 ≥ γ2 ≥ 0
i γ3 ≥ γ4 ≥ 0.
Matrica Q̃ ima jedinične retke i stupce. Stoga je suma kvadrata elemenata
svakog retka i svakog stupca jednaka jedan. To nam daje 8 jednadžbi, koje
slijede iz oblika (6)
matrice Q̃, a koje zapisujemo kroz četiri relacije:
|
γ12 + a2 + b2 = 1 = γ12 + e2 + g2
| | (7) |
|
γ22 + c2 + d 2 = 1 = γ22 + f 2 + h2
| | (8) |
|
γ32 + a2 + c2 = 1 = γ32 + e2 + f 2
| | (9) |
|
γ42 + b2 + d 2 = 1 = γ42 + g2 + h2
| | (10) |
Budući da je Q̃ ortogonalna, različiti stupci i retci
međusobno su ortogonalni. To nam
daje 12 jednadžbi, koje zapisujemo kroz 6 relacija:
|
ef + gh = 0 = ac + bd
| | (11) |
|
γ1a + γ3e = 0 = γ1e + γ3a
| | (12) |
|
γ1b + γ4g = 0 = γ1g + γ4b
| | (13) |
|
γ2c + γ3 f = 0 = γ2 f + γ3c
| | (14) |
|
γ2d + γ4h = 0 = γ2h + γ4d
| | (15) |
|
ab + cd = 0 = eg + fh
| | (16) |
Iz relacija (7) -
(10), zbrajanjem prvih
i drugih dviju lijevih jednadžbi, slijedi
γ12 + a2 +
b2 + γ22 +
c2 + d 2 =
2 = γ32 +
a2 + c2 +
γ42 +
b2 + d 2,
pa je
|
γ12 + γ22 = γ32 + γ42.
| | (17) |
Da bi Q̃ bila Θ, trebalo bi biti
|
γ1 = γ3 ≥ 0, e = −a ≥ 0
γ2 = γ4 ≥ 0, h = −d ≥ 0
|
, b = c = f = g = 0.
|
| | (18) |
Promotrimo prvo slučaj 1 > γ1 > 0 .
Pretpostavimo da je γ1 ≠ γ3.
Tada relacija (12)
daje
| a = − |
|
e, e = − |
|
a, pa je a = |
|
a, e = |
|
e, odakle slijedi
a = 0, e = 0. |
Ako uvrstimo uvjete a = 0 i
e = 0 u
relaciju (7)
i iskoristimo pretpostavku
γ1 < 1, dobijemo
b2 =
1 − γ12 =
g2 > 0,
pa je |b| = |g| > 0.
Sada relacija (13) povlači
|
|
= − |
|
, odakle slijedi γ4 = γ1 i g = −b. |
Sada relacija (11)
daje gh = 0 = bd, pa je h = 0 = d.
Pogledajmo relacije (8)
i (9).
Vidimo da mora biti: γ22 =
1 − c2 =
γ23, pa je γ2 = γ3.
Zapravo smo dobili γ4 = γ1 ≥ γ2 = γ3.
Zbog γ3 ≥ γ4,
to znači γ4 = γ3. Međutim, to ne može
biti, jer bi to značilo
γ1 ≥ γ3.
Za dobivenu kontradikciju kriva je pretpostavka
γ1 ≠ γ3, pa mora biti
γ1 = γ3.
Dakle, mora vrijediti
γ1 = γ3,
pa relacija (17) odmah daje
γ2 = γ4. Sada
imamo dvije mogućnosti:
γ1 = γ2 ili
γ1 > γ2.
Pretpostavimo da vrijedi
γ1 = γ2. U tom slučaju zapravo vrijedi
γ1 = γ2 = γ3 = γ4,
pa stavimo
γ = γi, za i = 1, 2, 3, 4.
Pritom vrijedi 0 < γ < 1.
Relacije (12) -
(15)
povlače: a = −e, b = −g,
c = −f, d = −h. S druge strane,
oduzimanjem
jednadžbe (7)
od (10),
pa opet (7)
od (9),
dobivamo a2 = d 2, b2 = c2,
tj. |a| = |d| i |b| = |c|. Pretpostavimo da je a ≠ 0.
Tada relacije (11)
i (16)
daju dvije mogućnosti: ako je d = a, tada je
c = −b i
ako je d = −a, tada je c = b.
Prema tome Q̃ može imati jedan od oblika
| Q̃ = |
|
| γ | 0 | a | b |
| 0 | γ | −b | a |
| −a | b | γ | 0 |
| −b | −a | 0 | γ |
| |
ili Q̃ = |
|
| γ | 0 | a | b |
| 0 | γ | b | −a |
| −a | −b | γ | 0 |
| −b | a | 0 | γ |
| |
. |
Da bi vrijedila relacija (18),
dovoljno je konstruirati rotaciju R, takvu da vrijedi
| R |
|
| |
= |
|
| |
|
|
| |
= |
|
| |
, σ = √a2 + b2, tan α = |
|
. |
Kad se iz tan α izračunaju cos α i sin α, još se izračuna i reflektor
Da bi matrica Q̃ iz relacije (6)
poprimila traženi oblik matrice Θ iz
relacije (3),
potrebno je u prvom slučaju (d = a i c = −b) zamijeniti matrice
U22 i V22 s
U22Rτ i
V22Rτ, a u drugom slučaju
(d = −a i c = b) zamijeniti matrice
U22 i V22 s
U22R̃τ i
V22R̃τ.
Provjerite matričnim množenjem da se u oba slučaja dobije matrica
Promotrimo sada slučaj γ1 > γ2.
Kako vrijedi
γ1 = γ3 i
γ2 = γ4, proučimo
prvo slučaj kad je
γ2 = γ4 = 0.
Relacije (12),
(13) i (15)
svode se na e = −a, b = 0 = g,
c = 0 = f,
respektivno. Zato relacije
(7) - (10)
daju |a| =
√1 − γ12 > 0,
|d| = |h| = 1.
Dakle je
gdje je d = ±1, h = ±1.
Da bi Q̃ postala Θ, potrebno je zamijeniti matrice
U22
i V22 s U22J i
V22J̃,
respektivno, gdje je
Neka je sada γ2 = γ4 > 0.
Relacije (12)
i (15) kraćenjem s
γ1, odnosno
γ2, daju
e = −a i h = −d. Sada
relacije (7)
i (8) daju
|b| = |g| i |c| = | f |. Oduzimanjem
jednadžbi u relaciji (7)
od onih u relaciji (9)
dobivamo |c| = |b|,
|g| = | f |.
Dakle, vrijedi: |b| = |c| = | f | = |g|.
Sada iz relacije (13) slijedi
| b = − |
|
g i |
g = − |
|
b, pa je b = |
|
b, odnosno ( | 1 − |
|
) b = 0. |
Dakle b = 0, a to znači i c = f = g = 0.
Stoga Q̃ ima oblik kao u
relaciji (19),
uz dodatni uvjet h = −d. Da bi
Q̃ postala Θ, potrebno je
zamijeniti matrice U22 i V22 s
U22J'
i V22J', gdje je
Preostaje razmotriti slučajeve
γ1 = 0 i
γ1 = 1.
Neka je
γ1 = 0 .
Sada je nužno zbog relacije (17),
γ1 = γ2 = γ3 = γ4 = 0.
Relacije (7) - (16)
pokazuju da su
proizvoljne ortogonalne matrice reda dva. S obzirom da je
bit će potrebno matrice U11 i U22
iz relacije (5)
zamijeniti s −U11W1
i U22W2,
respektivno.
Konačno, neka je
γ1 = 1 .
Iz relacija (7)
slijedi a = b = e = g = 0.
Pokažimo da je i
γ3 = 1. Kad
bi bilo
γ3 < 1, tada relacija (9)
povlači |c| = | f | > 0.
Stoga možemo dijeliti s c,
pa podijelimo jednadžbe u relaciji (14)
s c. Ako su c i f istog predznaka, tada
slijedi
γ2 + γ3 = 0, pa je
γ2 = 0 i γ3 = 0.
Zbog γ3 ≥ γ4
odmah slijedi
γ4 = 0, a
to se protivi relaciji (17).
Ako su c i f različitog
predznaka, tada relacija (14) daje
γ2 = γ3 i
f = −c.
Sada relacija (17) daje
γ4 = 1. Budući da je
γ3 < 1, dobili smo
γ3 < γ4, a to je nemoguće.
Dakle, pretpostavka
γ3 < 1 vodi u proturječje, pa
mora biti
γ3 = 1. No,
γ3 = 1 i relacija (9)
daje f = c = 0.
Također, relacija (17) daje
γ2 = γ4. Ortogonalna matrica Q ima oblik
|
| Q̃ = |
|
| |
, pri čemu je γ2 ≥ 0. |
| | (20) |
Ako je
γ2 > 0, relacija (15)
implicira
h = −d. Tada Θ nastaje iz Q̃
ako U22 i
V22 iz relacije (5)
zamijenimo s U22J'' i
V22J'', gdje je
Ako je
γ2 = 0, tada relacija (8)
pokazuje da vrijedi
|d| = |h| = 1. Sada Θ
nastaje iz Q̃ ako U22 i V22
iz relacije (5)
zamijenimo s U22J''' i
V22J'', gdje je
J'' kao u (21), a
4.2 Q11 je reda jedan
Izračunajmo singularnu dekompoziciju podmatrice Q22,
Q22 = U22Γ2V22τ
i sagradimo ortogonalne matrice
Množenjem se dobije
| Q̃ = Uτ QV = |
|
| |q11| | Q12V22 |
| U22τQ21 | U22τQ22V22 |
| |
= |
|
| |
|
| = |
|
| | , |
γ1 ≥ 0,
γ2 ≥ γ3 ≥ γ4 ≥ 0. |
| | (22) |
Pritom je γ1 = |q11| jedina singularna vrijednost od Q11, dok su
γ2, γ3, γ4 singularne vrijednosti od
Q22. Kako izračunati singularnu dekompoziciju matrice
reda 3 izlazi iz okvira ovog rada (vidjeti [GO]). Slučajeve kad je Q11 reda 1 i reda
3 ionako nećemo koristiti u primjenama CS dekompozicije u ovom radu.
Ortogonalnost matrice Q daje relacije
|
γ12 + a2 + b2 + c2 = 1 = γ12 + e2 + f 2 + g2
| | (23) |
|
γ22 + a2 = 1 = γ22 + e2
| | (24) |
|
γ32 + b2 = 1 = γ32 + f 2
| | (25) |
|
γ42 + c2 = 1 = γ42 + g2
| | (26) |
γ1 e + γ2 a = 0 = γ1 a + γ2 e
γ1 f + γ3 b = 0 = γ1 b + γ3 f
|
γ1 g + γ4 c = 0 = γ1 c + γ4 g
| | (27) |
Prvo pokažimo da mora biti a = 0. Kad bi bilo
a ≠ 0,
tada bi zbog relacija (28)
i (29),
moralo vrijediti b =0 = c,
a onda bi zbog (25)
i (26) bilo
γ3 = 1 = γ4.
Budući da je zbog (24)
γ2 = √1 − a2 < 1,
dobili bismo kontradikciju s
pretpostavkom (22) da je
γ2 ≥ γ3 ≥ γ4.
Budući da je a = 0, zbog lijeve jednadžbe
u (24) mora biti
γ2 = 1, a onda zbog
desne jednadžbe e = 0.
Relacija (30)
pokazuje da mora biti b = 0 ili c = 0.
Zbog relacije
γ3 ≥ γ4 i
relacija (25)
i (26), mora
svakako biti b = 0.
Ako je i c = 0, tada
relacije (25),
(26)
i (23) pokazuju da je
Q̃ = I4 jedinična
matrica reda 4, koja se uklapa u oblik od Θ.
Ako je c ≠ 0, onda je
γ1 = √1 − c2 = γ4,
pa relacija (27) pokazuje da je
g = −c. Tada je
pa još treba osigurati da je −c ≥ 0.
To se postiže tako da se
zadnji redak i
stupac od Q̃, odnosno zadnji stupac od U22 i od
V22 pomnoži sa −sign(c).
4.3 Q11 je reda tri
Taj slučaj može se svesti na prethodni korištenjem transformacije sličnosti
sa specijalnom permutacijom. Ipak, zbog cjelovitosti prikaza i zbog korištenja
što manjeg obujma iz teorije matrica, načinit ćemo cjelovitu analizu.
Izračunajmo singularnu dekompoziciju podmatrice Q11,
Q11 = U11Γ1V11τ
i sagradimo ortogonalne matrice
Množenjem se dobije
| Q̃ = UτQV = |
|
| U11τ Q11V11 | U11τ Q12 |
| sign(q44)Q21 | |q44| |
| |
= |
|
| |
|
| = |
|
| |
, |
γ1 ≥ γ2 ≥ γ3 ≥ 0,
γ4 ≥ 0. |
| | (31) |
Pritom je
γ4 = |q44| jedina singularna vrijednost
od Q22, dok su
γ1, γ2 i γ3
singularne vrijednosti od Q11.
Ortogonalnost matrice Q daje relacije
|
γ12 + a2 = 1 = γ12 + e2
| | (32) |
|
γ22 + b2 = 1 = γ22 + f 2
| | (33) |
|
γ32 + c2 = 1 = γ32 + g2
| | (34) |
|
γ42 + a2 + b2 + c2 = 1 = γ42 + e2 + f 2 + g2
| | (35) |
γ1 e + γ4 a = 0 = γ1 a + γ4 e
γ2 f + γ4 b = 0 = γ2 b + γ4 f
|
γ3 g + γ4 c = 0 = γ3 c + γ4 g
| | (36) |
Prvo pokažimo da mora biti a = 0. Kad bi bilo a ≠ 0,
tada bi zbog relacija (37)
i (38)
moralo vrijediti b = 0 = c,
a onda bi zbog (33)
i (34)
bilo
γ2 = 1 = γ3.
Budući da je zbog (32)
γ1 = √1 − a2 < 1,
dobili bismo kontradikciju s pretpostavkom (31)
da je
γ1 ≥ γ2 ≥ γ3.
Budući da je a = 0, mora po
relaciji (32) biti
γ1 = 1, a onda također i e = 0.
Relacija (39)
pokazuje da mora biti b = 0 ili c = 0.
Zbog relacije
γ2 ≥ γ3 i
relacija (33),
(34),
mora svakako biti b = 0.
Ako je i c = 0, onda relacije (33)
i (34) pokazuju da je
Q̃ = I4
jedinična matrica reda 4 koja se uklapa u oblik od Θ.
Ako je c ≠ 0, onda je
γ3 = √1 − c2 = γ4,
pa relacija (36) pokazuje da je
g = −c. Tada je
pa još treba osigurati da je −c > 0. To se postiže
tako da se zadnji
redak i stupac od Q̃ te zadnji stupac od U22 i od
V pomnože sa −sign(c).
5. Jedna primjena CS dekompozicije
Iz teorije matrica poznato je da se svaka simetrična matrica A
reda n može prikazati u obliku
A = QΛQτ,
pri čemu je Q
ortogonalna matrica, a
Λ = diag(λ1,…,λn)
dijagonalna matrica.
Stupci matrice Q čine ortonormiran sistem vlastitih vektora, a dijagonalni
elementi λ1,...,λn matrice Λ su vlastite
vrijednosti od A. Takav rastav zove se
spektralni rastav (ili dekompozicija) simetrične matrice. Zbog
Λ = QτAQ, kaže
se da Λ nastaje iz A transformacijom sličnosti pomoću matrice Q.
Za potrebe ubrzavanja tzv. dijagonalizacijskih metoda za računanje
spektralnog rastava simetrične matrice reda n, javlja se problem što
točnijeg i bržeg računanja spektralnih rastava simetričnih matrica
malih dimenzija. Ovdje ćemo pokazati kako nas CS dekompozicija ortogonalnih matrica
dimenzija 3 i 4 upućuje na smjer u kojem treba nastaviti istraživanje, za
nalaženje što efikasnijeg i točnijeg algoritma za simetrične matrice
reda 3 i 4.
5.1. Dijagonalizacija simetrične matrice reda 3
Neka je Q ortogonalna matrica reda 3. Tada su
njene CS dekompozicije. Vidimo da se svaka ortogonalna matrica Q reda 3
može prikazati kao produkt od tri ravninske rotacije. Prvi red zadnje relacije
pokazuje da je
Q = Φ1R12(ψ1)R23(ψ2)R12(ψ3)Φ2, ψ2 = θ,
gdje su Φ1 i Φ2 dijagonalne matrice predznaka.
Kako Φ2 ne utječe na dijagonalizaciju jer je
Φ1DΦ1 = D za svaku dijagonalnu matricu D,
problem se svodi na traženje što efikasnijeg i točnijeg algoritma za
računanje kutova ψ1, ψ2 i ψ3.
Drugi red iste relacije pokazuje da Q možemo tražiti u obliku
Q = Φ1R23(ψ1)R13(ψ2)R23(ψ3)Φ2.
Dakle, tražena ortogonalna matrica može se prikazati u obliku triju ravninskih
rotacija (i jedne dijagonalne matrice predznaka). Drugim riječima, simetrična
matrica reda 3 može se dijagonalizirati korištenjem samo triju rotacija. Pritom
o rotacijama znamo u kojem redoslijedu i u kojim ravninama rotiraju, ali ne
znamo jednostavno izračunati kutove. Nalaženje efikasnog algoritma za brzo i
točno računanje tih kutova na računalima zanimljiv je istraživački
problem.
5.2. Dijagonalizacija simetrične matrice reda 4
Ovdje ćemo na sličan način pokazati da se simetrična matrica reda 4
može dijagonalizirati pomoću 6 rotacija i o rotacijama znamo sve (u kojem redoslijedu
i u kojim ravninama rotiraju) osim kutova. Promatrat ćemo samo slučaj kad
je gornja vodeća podmatrica Q11 reda 2. Ostale particije, kad je
Q11 reda 1
ili 3, daju nepovoljniji krajnji rezultat, koji uključuje 8 rotacija, pa ih nećemo
razmatrati.
Relacija (2) se za ortogonalnu matricu reda 4 može zapisati kao
pri čemu je ci = cos ψi,
si = sin ψi za
i = 1,…,6. Ako su
| A = |
|
| | |
i Q takve da je A = QΛQτ |
, |
tada Φ1 i prve dvije rotacije "pripremaju teren" za sljedeće dvije
rotacije koje moraju "poništiti" cijeli blok koji čine elementi
a13, a14, a23 i a24.
Dakle prve 4 rotacije, transformacijama sličnosti na A, trebaju pretvoriti te
elemente u nulu.
To mora biti tako, jer zadnje dvije rotacije ne mijenjaju normu (korijen iz sume
kvadrata elemenata) tog bloka. Pa ako on nije postao nul-matrica prije primjene
zadnjih dviju rotacija, i na kraju će ostati takav, različit od nul-matrice. Stoga,
zadnje dvije rotacije pretvaraju u nule elemente na pozicijama elemenata a12 i
a34. Zadnja dijagonalna matrica predznaka Φ2 nije potrebna iz gore spomenutih
razloga.
U zaključku napominjemo da smo uz prikaz CS dekompozicije ortogonalnih
matrica do reda 4, otvorili i problem brzog računanja spektralne dekompozicije
simetričnih matrica reda 3 i 4. Pritom smo dali upute o minimalnom broju i
redoslijedu rotacija s obzirom na ravnine u kojima rotiraju. Algoritam za direktno
računanje pripadnih rotacijskih kutova ψi izazovan je istraživački problem.
Autori zahvaljuju anonimnim recenzentima na korisnim primjedbama koje
su poboljšale kvalitetu ovog rada.
Literatura
|
[GO] |
G.H. Golub i C.F. Van Loan, Matrix Computations, The Johns
Hopkins University Press, drugo izdanje, 1989. |
| [ZA] |
V. Zadelj-Martić, Singularna dekompozicija matrice reda dva,
Matematičko-fizički list (prihvaćeno za objavljivanje). |
1. Uvod u kosinus-sinus dekompoziciju
2. Singularna dekompozicija matrice reda dva
3. CS dekompozicija ortogonalnih matrica reda 2 i 3
4. CS dekompozicija ortogonalne matrice reda 4
5. Jedna primjena CS dekompozicije
Literatura




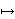 Ax = UΞVτ x:
prvo se x rotira u vektor Vτ x, zatim se
komponente od Vτ x
pomnože nenegativnim brojevima α1 i α2, te se dobije
vektor ΞVτ x. Konačno,
ΞVτ x se rotira matricom U.
Budući da množenje s Vτ i U ne mijenja normu
vektora, norma od Ax ovisi jedino o singularnim vrijednostima matrice A. Isti
zaključak vrijedi i kad je A višeg reda.
Ax = UΞVτ x:
prvo se x rotira u vektor Vτ x, zatim se
komponente od Vτ x
pomnože nenegativnim brojevima α1 i α2, te se dobije
vektor ΞVτ x. Konačno,
ΞVτ x se rotira matricom U.
Budući da množenje s Vτ i U ne mijenja normu
vektora, norma od Ax ovisi jedino o singularnim vrijednostima matrice A. Isti
zaključak vrijedi i kad je A višeg reda.