Sadržaj:

1. Uvod
2. Permutacije
3. Ispitivanje rješivosti slagalice
4. Metoda rješavanja
5. Komentar
6. Zadaci
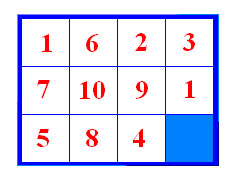
Literatura

1. Uvod

Amerikanac Sam Loyd (1841.-1911.) bio je jedan od najpoznatijih sastavljača zagonetki i šahovskih problema svoga vremena. Sa samo 14 godina počeo je objavljivati šahovske probleme, a već pet godina kasnije imao je zavidnu reputaciju na tom području. Jedan od njegovih najpoznatijih problema nesumnjivo je takozvani Boss puzzle (u nekim izvorima susreće se još i naziv "14-15 puzzle in Puzzleland"), slagalica od 15 kvadratića i jednog praznog polja. Kvadratići s brojevima mogu se pomicati korištenjem praznog polja, a cilj igre je poredati ih od 1 do 15. Davne 1878. Loyd je ponudio 1000 dolara nagrade onome tko prvi uspije složiti slagalicu u kojoj su zamijenjeni kvadratići 14 i 15 dok se ostali nalaze na svojim mjestima.

Zadatak se brzo proširio Amerikom, a stigao je i do Europe. Mnogi su gubili vrijeme i živce, ali problem svejedno nije riješen. Neki su čak tvrdili da su uspjeli riješiti slagalicu, ali nisu znali rekonstruirati poteze kojima su je riješili. Nagrada od 1000 dolara nije nikome isplaćena. Loyd je, naravno, znao da slagalica s takvim rasporedom kvadratića nije rješiva pa je velikodušno ponudio novce prvom rješavaču ovog naoko lakog problema. Obrat u priči javlja se tek kada je Sam Loyd pokušao patentirati svoj izum. Tada je bilo potrebno, da bi se patentirao neki uređaj, konstruirati jedan njegov primjerak koji će ispravno raditi. Zbog toga Loydu nije dopušteno patentirati Boss puzzle uz obrazloženje: Kako je moguće napraviti model slagalice koja će ispravno raditi kada je poznato da takva slagalica ne radi, tj. da se ne može riješiti (složiti).

U članku ćemo pokazati zašto nitko nije uspio riješiti Loydov problem. U prvom dijelu navedene su neke osnovne činjenice o permutacijama koje ćemo kasnije koristiti, u drugom dijelu tražimo uvjete za rješivost slagalice, a u trećem smo razvili jednu metodu njezinog rješavanja.

2. Permutacije

Pojam permutacije javlja se u mnogim granama matematike. Susrećemo ga, na primjer, u teoriji grupa, kombinatorici, linearnoj algebri. Osim u matematici na permutacije možemo naići i u svakodnevnom životu, npr. uzmimo skup karata za "belu":

Prije početka igre jedan od igrača promiješat će karte, čime će promijeniti njihov redoslijed u špilu. Što se zapravo dogodilo? Imali smo 32 karte poredane nekim redoslijedom. Znamo koja se nalazi na prvom mjestu (vrh špila), koja na drugom mjestu itd. Jedan igrač je uzeo špil karata sa stola, promiješao ih i vratio na stol (pretpostavimo da je vratio sve karte). Dakle, opet imamo 32 karte, samo što se na prvom mjestu (možda) nalazi neka druga karta, na drugom neka druga itd. Promjenu redoslijeda karata možemo promatrati kao funkciju. Funkcija uzima redom karte i miješa ih, odnosno mijenja njihov redoslijed – karti koja se nalazila na početku na prvom mjestu pridružuje neku drugu kartu koja će se nakon miješanja naći na prvom mjestu, karti koja je bila na drugom mjestu pridružuje kartu koja će se nakon miješanja naći na drugom mjestu itd. Takvu funkciju zvat ćemo permutacijom.

Neka je n prirodan broj i S skup od n elemenata. Permutaciju na S definiramo kao bijekciju p : S → S.

U našem primjeru je n=32 jer imamo 32 karte. Skup S je skup karata. Provjerimo je li "funkcija koja miješa karte" bijekcija. Injektivnost znači da prije miješanja ne postoje dvije karte kojima će se nakon miješanja pridružiti ista karta. Uzmimo dvije različite karte, npr. 7♠ i 9♥, i neka je prije miješanja sedmica na prvom, a devetka na dvadesetom mjestu u špilu. Kako god promiješali karte, ne postoji karta koja će se nakon miješanja naći istovremeno na prvom i na dvadesetom mjestu. Preostaje nam provjeriti surjektivnost. Mora vrijediti da za svaku kartu iz špila postoji neka druga karta kojoj je ona pridružena. To znači da ako se nakon miješanja neka karta nalazi npr. na 23. mjestu, onda je i prije miješanja postojala neka karta koja je bila na 23. mjestu. Kako imamo 32 karte, kad ih počnemo brojati (počevši od vrha), prije ili kasnije ćemo doći na kartu koja se nalazi na 23. mjestu. Dakle, pokazali smo da je naša funkcija bijekcija pa je po definiciji ona permutacija.

Uobičajeno je sa S_n označavati skup svih permutacija skupa od n elemenata. Dakle, ako permutaciju koja je miješala karte označimo sa p, onda vrijedi p ∈ S_n. Primijetimo još da nam je ovdje bitan samo broj 32, nije bitno što se nalazi u skupu na kojem permutacija djeluje i kakvi su odnosi među elementima – važno je da ih razlikujemo, npr. možemo definirati N₃:={1,2,3} pa promatrati permutacije na tom skupu. Permutaciju možemo zapisati na sljedeći način:

Radi se o permutaciji na skupu N₃. Iz prvog stupca matrice čitamo da se broj 1 preslika u 2, iz drugog stupca da se broj 2 preslika u 3, a iz trećeg da se broj 3 preslika u 1. U prethodnom primjeru s kartama to bi značilo da imamo tri karte te da će se karta koja je prije miješanja bila na vrhu (prvo mjesto) naći nakon miješanja na drugom mjestu, ona koja je bila na drugom mjestu nakon miješanja otići na treće, a ona koja je bila na trećem mjestu nakon miješanja će se naći na vrhu.

Nakon što je igrač promiješao karte, mogli bismo se zapitati na koliko je on to načina mogao učiniti, tj. koliko je različitih ishoda (rasporeda karata) mogao dobiti. Za odgovor na to pitanje uzmimo dio iz špila karata za remi (as je označen jedinicom):

Pitanje je na koliko različitih načina možemo rasporediti tih 13 karata. Odgovor nam daje sljedeća propozicija.

Propozicija. Svih permutacija skupa od n elemenata ima n! = 1·2·3·…·n.

U našem slučaju to znači da karte možemo rasporediti na 13! = 6227020800 načina. Pogledajmo kako je taj broj dobiven. Znamo da će se, kako god ispermutirali karte, jedna i samo jedna naći na prvom mjestu, drugom, trećem,… Ako imamo 13 karata, tada na 13 različitih načina možemo odabrati koju ćemo kartu staviti na prvo mjesto jer možemo uzeti bilo koju od njih. Nakon što smo stavili neku kartu na prvo mjesto, biramo koju ćemo staviti na drugo. Preostalo nam je još 12 karata pa tu kartu možemo odabrati na 12 načina. Prvo i drugo mjesto zajedno možemo popuniti na 13·12 načina. Kartu koja će se nalaziti na trećem mjestu biramo na 11 načina pa prva tri mjesta možemo popuniti na 13·12·11 načina. Na kraju dolazimo do broja 13·12·11·…·3·2·1 = 13!.

Za idući primjer uzet ćemo samo jednu kartu i rotirati je za 0°, 120°, 240° u pozitivnom smjeru kao što je prikazano na slici.

Za rotacije 0°, 120°, 240° uvedimo redom oznake a, b, c. Skup koji sadrži te tri rotacije označimo s A. Uočimo prvo da komponiranjem bilo kojih dviju rotacija iz A opet dobivamo rotaciju iz A, npr. b◦c = a, tj. ako kartu rotiramo za 240 pa za 120 stupnjeva, dobili smo isti rezultat kao da smo je rotirali za 360 stupnjeva, odnosno kao da je uopće nismo rotirali.

Dalje vidimo da se komponiranje rotacija iz A otprilike svodi na zbrajanje modulo 360. Ako provedemo tri rotacije za 120 stupnjeva pa dvije za 240 stupnjeva imamo

što je rotacija b. Kako je zbrajanje asocijativno, (x + y) + z = x + (y + z), zaključujemo da je i komponiranje rotacija asocijativno.

Promotrimo rotaciju a. Ona zapravo ništa ne radi – ako rotiramo kartu za 0 pa za 120 stupnjeva, dobili smo isti ishod kao i da smo je samo rotirali za 120 stupnjeva. To možemo zapisati kao a◦b = b◦a = b (nije bitno kojim redoslijedom provodimo rotacije). Analogno je a◦c = c◦a = c.

Ako provedemo rotaciju b pa zatim rotaciju c, dobivamo rotaciju a, tj. nismo promijenili položaj karte. Dakle, imamo b◦c = c◦b = a.

Ako s G označimo skup A koji sadrži tri rotacije karte, a s ◦ operaciju komponiranja tih rotacija, iz prethodnih razmatranja vidimo da (A,◦) zadovoljava sva četiri zahtjeva iz definicije:

1. Komponiranjem dviju rotacija dobivamo rotaciju. Ovo svojstvo se često naziva zatvorenost (jer komponiranjem elemenata skupa G ne možemo izaći iz njega pa kažemo da je zatvoren s obzirom na tu operaciju).
2. Ovo svojstvo se zove asocijativnost i već smo ga provjerili.
3. Ulogu elementa e ∈ G iz definicije preuzela bi rotacija za 0 stupnjeva, tj. a ∈ A. Element e, odnosno u našem slučaju a, zovemo neutralnim elementom.
4. Već smo vidjeli da vrijedi b◦c = c◦b = a pa je b^-1 = c. Kažemo da je c inverz od b. Također je c^-1 = b pa je b inverz od c.

Nisu sve grupe konačne. Skup svih cijelih brojeva s obzirom na zbrajanje primjer je jedne beskonačne grupe.

Propozicija. Skup S_n svih permutacija od n elemenata je grupa.

Prethodno smo definirali grupu kao uređen par skupa i binarne operacije na tom skupu, a ovdje tvrdimo da sam skup čini grupu. To je, na prvi pogled, malo neispravno, ali se koristi iz praktičnih razloga ako je jasno o kojoj se operaciji radi. Kako je prirodna operacija na S_n komponiranje, mi zapravo tvrdimo da je (S_n,◦) grupa.

Tvrdnju nećemo dokazivati, nego ćemo je samo komentirati.

1. Kompozicija dviju permutacija je permutacija. Ako se vratimo na prvi primjer s kartama, to bi značilo da ako igrač dva puta promiješa karte i dobije neki redoslijed, onda ih je mogao otprve promiješati tako da dobije taj isti redoslijed. Ono što je postigao s dva miješanja mogao je postići samo jednim, nekim drugim miješanjem.
2. Uzmimo karte 1♠, 2♠, 3♠, 4♠, 5♠. Neka je m₁ permutacija koja zamjenjuje prve dvije karte, m₂ permutacija koja zamjenjuje drugu i treću kartu, m₃ permutacija koja zamjenjuje treću i četvrtu kartu. Ako provedemo m₃, dobivamo redoslijed 1♠, 2♠, 4♠, 3♠, 5♠. Kompoziciju m₂◦m₃ dobiti ćemo tako da na tom redoslijedu karata provedemo m₂. Dobije se 1♠, 4♠, 2♠, 3♠, 5♠. Tvrdnja 2 kaže da ako na dobivenom redoslijedu karata provedemo m₁, dobivamo isto što i ako na 1♠, 2♠, 4♠, 3♠, 5♠ provedemo m₁◦m₂, tj. m₁◦(m₂◦m₃) = (m₁◦m₂)◦m₃. Lako se provjeri da u jednom i u drugom slučaju dobivamo 4♠, 1♠, 2♠, 3♠, 5♠.
3. Tvrdnja kaže da postoji neutralni element, tj. permutacija koja ništa ne radi. Takva je permutacija jedinstvena. Neutralni element u S₃ je permutacija

   e =

   ( 1   2   3 ) 1   2   3

   .

   U primjeru s kartama neutralni element ostvarili bismo tako da uzmemo špil karata sa stola i vratimo ih na stol - nismo promijenili redoslijed karata.
4. Za permutaciju

   r =	( 1   2   3 ) 2   3   1

   inverzni će element biti

   r-1 =

   ( 1   2   3 ) 3   1   2

   .

   Vidimo da je r(1) = 2 i r^-1(2) = 1, što možemo zapisati kao (r^-1◦r)(1) = 1 = e(1), gdje je e neutralni element. Kod primjera s kartama inverzna permutacija je ona koja će karte, nakon što ih promiješamo, vratiti u početni raspored. Dakle, ako je prilikom miješanja 17. karta dospjela na treće mjesto, onda inverzno miješanje, tj. permutacija, šalje treću kartu na 17. mjesto.

Vidjeli smo da skup permutacija n-članog skupa ima ista svojstva kao i grupa rotacija karte koju smo definirali. Ipak, postoji jedna bitna razlika. Kod grupe rotacije karte vidjeli smo da se komponiranje rotacija svodi na zbrajanje modulo 360 pa je, zbog komutativnosti zbrajanja, to komutativna grupa. To znači da za svake dvije rotacije dobivamo isti rezultat prilikom njihovog komponiranja, neovisno o tome koja je prva, a koja druga. Rotacijom karte za 120° pa za 240° dobili smo isto što bismo dobili da smo prvo proveli rotaciju za 240° pa zatim onu za 120°.

Za razliku od grupe rotacija karte, grupa permutacija nije komutativna. Pokazat ćemo to jednim kontraprimjerom. Uzmimo karte 1♠, 2♠, 3♠, 4♠, 5♠ i prethodno definirane permutacije m₁ i m₂. Računamo m₂◦m₁. Nakon provođenja m₁ (zamjenom prvih dviju karata) dobivamo 2♠, 1♠, 3♠, 4♠, 5♠. Provođenjem m₂, tj. zamjenom druge i treće karte dobivamo 2♠, 3♠, 1♠, 4♠, 5♠.

Računamo m₁◦m₂. Provodimo prvo m₂ na 1♠, 2♠, 3♠, 4♠, 5♠ i dobivamo 1♠, 3♠, 2♠, 4♠, 5♠. Zatim slijedi m₁ (zamjena prvih dviju karata): 3♠, 1♠, 2♠, 4♠, 5♠. Očito ne dobivamo isti raspored karata kao za m₂◦m₁.

Inverzijom permutacije p ∈ S_n nazivamo svaki uređeni par (i,j) takav da je i < j i p(j) > p(i).

Uzmimo sedam karata, 2♥, 3♥, 4♥, 5♥, 6♥, 7♥, 8♥ i promiješajmo ih tako da se dobije raspored 3♥, 5♥, 6♥, 8♥, 4♥, 7♥, 2♥. Permutaciju označimo s p. Dakle, vrijedi p(2♥) = 3♥, p(3♥) = 5♥, p(4♥) = 6♥, p(5♥) = 8♥, p(6♥) = 4♥, p(7♥) = 7♥ i p(8♥) = 2♥. Primijetimo da je 5♥ < 6♥, ali p(5♥) = 8♥ > 4♥ = p(6♥). Dakle, (5♥, 6♥) je jedna inverzija. Preostale inverzije su (2♥, 8♥), (3♥, 6♥), (3♥, 8♥), (4♥, 6♥), (4♥, 8♥), (5♥, 7♥), (5♥, 8♥), (6♥, 8♥) i (7♥, 8♥).

Za permutaciju kažemo da je (ne)parna ako ima (ne)paran broj inverzija.

Prema definiciji, permutacija p je parna jer ima deset inverzija. Uočimo da je neutralni element iz S_n uvijek parna permutacija jer ima nula inverzija. Može se dokazati da ima jednako mnogo parnih i neparnih permutacija, tj. da ih ima točno n!/2.

Za zbrajanje prirodnih brojeva vrijedi da je zbroj dvaju brojeva iste parnosti paran, a zbroj dvaju brojeva različite parnosti neparan broj. Slična tvrdnja vrijedi i za permutacije. Komponiranjem permutacija iste parnosti dobivamo parnu, a komponiranjem permutacija različite parnosti neparnu permutaciju.

Može se dokazati da je inverz (ne)parne permutacije opet (ne)parna permutacija. Iz toga slijedi da skup svih parnih permutacija skupa od n elemenata čini grupu. Skup neparnih permutacija ne čini grupu jer ne sadrži neutralni element koji je paran.

Promotrimo sljedeću situaciju. Špil od 13 karata, 1♣, 2♣, 3♣, 4♣, 5♣, 6♣, 7♣, 8♣, 9♣, 10♣, J♣, Q♣, K♣ nalazi se na stolu. Na vrhu je karta 1♣, ispod nje karta 2♣ i tako dalje. Izvucimo kartu 7♣ i stavimo je na vrh špila. Dobili smo sljedeći rapored: 7♣, 1♣, 2♣, 3♣, 4♣, 5♣, 6♣, 8♣, 9♣, 10♣, J♣, Q♣, K♣.

Što se dogodilo s rasporedom karata? Karta 1♣ našla se na mjestu na kojem se nalazila karta 2♣, karta 2♣ našla se na mjestu na kojem se nalazila karta 3♣… Karta 7♣ došla je na prvo mjesto, a karte 8♣, 9♣, 10♣, J♣, Q♣ i K♣ ostale su na istim mjestima. Permutaciju koja na opisani način razmješta elemente zovemo ciklusom.

Vidimo da je izvlačenje karte 7♣ i njezino dovođenje na vrh bio ciklus duljine 7 (toliko je karata promijenilo svoj položaj). Važno je napomenuti da je li neka permutacija ciklus ili nije, ne ovisi o redoslijedu kojim smo zapisali elemente na koje ona djeluje. Npr. uzmimo permutaciju

Opet imamo ciklus, ali sada duljine 3. Razlika u odnosu na prošli primjer u tome je što to sada nije tako očito, tj. nemamo neku lijepu interpretaciju (izvlačenje jedne karte i njezino stavljanje na vrh). Ipak, vidimo da se jedinica preslika u trojku, trojka u peticu, petica u jedinicu pa je to zaista ciklus duljine 3. Naravno, permutaciju q možemo zapisati i kao

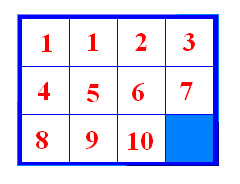
iz čega se odmah vidi da se radi o ciklusu.

Cikličku permutaciju iz prethodne definicije kraće zapisujemo kao (i₁  i₂  …  i_d). Ovim načinom zapisa gornji ciklus duljine 3 zapisali bismo kao q = (1 3 5), a permutaciju iz primjera uoči definicije kao (1♣  2♣  3♣  4♣  5♣  6♣  7♣).

Ciklus duljine 2 zovemo transpozicijom.

Teorem. Ciklusi s parnim brojem elemenata su neparne, a ciklusi s neparnim brojem elemenata parne permutacije.

Prema ovom teoremu ciklus q iz prethodnog primjera je parna permutacija. Zaista, on ima šest inverzija: (3,4), (3,5), (1,2), (4,5), (1,5) i (2,5).

Komponiranjem parnog broja transpozicija dobivamo parnu, a komponiranjem neparnog broja transpozicija neparnu permutaciju. Za ilustraciju uzmimo permutacije m₁ i m₂ na skupu {1♠, 2♠, 3♠, 4♠, 5♠}. Već smo vidjeli da ako s m₂◦m₁ djelujemo na 1♠, 2♠, 3♠, 4♠, 5♠, dobivamo 2♠, 3♠, 1♠, 4♠, 5♠; ako s m₁◦m₂ djelujemo na 1♠, 2♠, 3♠, 4♠, 5♠, dobivamo 3♠, 1♠, 2♠, 4♠, 5♠. U prvom i u drugom slučaju dobili smo parnu permutaciju koja ima dvije inverzije.

Ovo su sve činjenice o permutacijama koje će nam trebati prilikom rješavanja slagalice Boss puzzle. Posebno ćemo često koristiti zadnja dva teorema. Mnogo više o permutacijama može se saznati u nekoj od knjiga koje su navedene kao literatura. Dokazi tvrdnji koje smo ovdje naveli mogu se pronaći u [HO].

3. Ispitivanje rješivosti slagalice

Kao što je jasno iz naslova, u ovom ćemo poglavlju provjeravati kada je naša slagalica rješiva. Glavna ideja čitavog ovog poglavlja jest pridruživanje permutacije slagalici. Nakon što definiramo to pridruživanje, svest ćemo problem rješivosti slagalice na neke probleme s permutacijama. Oni se pak mogu riješiti korištenjem isključivo definicija i tvrdnji navedenih u prvom poglavlju. U dijelu u kojem definiramo permutaciju pridruženu slagalici nije sasvim jasno zašto je to pridruživanje provedeno baš na taj način. Jedan od razloga je to što se tada prilično lako može eliminirati čak polovica slagalica iz razmatranja jer se vidi da nisu rješive. S druge strane, drugačije definirano pridruživanje nas vjerojatno ne bi odvelo u krivom smjeru, štoviše, mogli bismo primijeniti isti dokaz. Dakle, nakon što relativno lako dokažemo da u barem polovici slučaja slagalica nije rješiva, tj. da nije rješiva kada je njoj pridružena permutacija neparna, preostaje nam još ispitati drugu polovicu, tj. što se događa kad je slagalici pridružena parna permutacija. U prvom poglavlju komentirali smo kako je parna permutacija kompozicija parnog broja transpozicija. Dalje dokazujemo da se kompozicija dviju transpozicija može zapisati kao kompozicija ciklusa duljine 3, koji se provode nad susjednim kvadratićima slagalice. Još samo preostaje vidjeti da se svaki ciklus duljine 3 nad susjednim kvadratićima slagalice može provesti i time smo dokazali rješivost slagalice. Ta posljednja tvrdnja dokazana je eksperimentalno i iz nje konačno slijedi da je slagalica rješiva ako i samo ako je njoj pridružena permutacija parna. Time smo problem ispitivanja rješivosti slagalice sveli na problem brojanja inverzija neke permutacije od 15 elemenata, što je ipak prilično lak zadatak.

Promatrat ćemo slagalicu s proizvoljnim rasporedom kvadratića, ali uz jedno malo ograničenje. Zbog jednostavnosti ćemo se baviti samo sa slagalicama kojima se prazno polje nalazi u desnom donjem uglu. Time ne smanjujemo općenitost jer kad se ono ne bi nalazilo na željenoj poziciji, uvijek bismo mogli provesti odgovarajuće pomake kvadratića tako da ga smjestimo u desni donji ugao. Kasnije ćemo vidjeti da na taj način ne možemo utjecati na rješivost slagalice pa je to zaista dopuštena pretpostavka.

Za slagalicu kažemo da je rješiva ako se nakon konačnog broja pomaka kvadratića oni mogu dovesti u položaj sa slike 1, tj. složiti uzlazno po recima.

Slika 1

Pod pomakom podrazumijevamo jednu zamjenu praznog polja i nekog kvadratića, npr. ako slagalici sa slike 1 pomaknemo kvadratić 15 udesno napravili smo jedan pomak.

Dogovorili smo se da se na početku slaganja prazno polje nalazi u desnom donjem uglu. Također, ako je slagalica rješiva, kad je riješimo, ono će se opet naći tamo. Pomicanje kvadratića po slagalici možemo interpretirati kao zamjenu određenog kvadratića i praznog polja, npr. pomicanje broja 12 sa slike 1 u desni donji ugao možemo shvatiti kao zamjenu broja 12 te praznog polja – broj 12 se našao na mjestu praznog polja, prazno polje na mjestu broja 12. Prema tome, tijekom slaganja mi pomičemo prazno polje po slagalici te ga na kraju vraćamo u donji desni ugao (odakle smo i krenuli). Iz toga vidimo da smo tijekom slaganja napravili paran broj pomaka. Tvrdnja možda i nije sasvim očita pa je možemo dokazati.

Za početak definirajmo neku varijablu, npr. c := 1. Kada prazno polje pomaknemo gore pomnožimo c s 2, kada prazno polje pomaknemo dolje, pomnožimo c s 1/2. Kada prazno polje pomaknemo udesno, pomnožimo c s 3, za pomak ulijevo množimo c s 1/3. Nakon što smo složili slagalicu, c opet ima vrijednost 1 (ako smo maksimalno skratili brojnik i nazivnik). Kada bi mu brojnik bio djeljiv npr. s 2, to bi značilo da smo tijekom slaganja prazno polje više puta pomicali prema gore nego prema dolje pa slagalica očito nije još složena (riješena) jer prazno polje nije u četvrtom retku. Analogno se prodiskutiraju i preostala tri slučaja. Dakle, nakon slaganja c doista ima vrijednost 1. Ako smo prazno polje pomaknuli tijekom slaganja g puta prema gore i d puta udesno, to znači da smo prazno polje ukupno pomaknuli 2(g + d) puta. Dakle, napravili smo paran broj pomaka.

Slagalici možemo pridružiti jednu permutaciju iz S₁₆. Mjesta na kojima se mogu naći kvadratići označimo brojevima od 1 do 16 kao na slici 2, prazno polje označimo brojem 16. Permutacija pridružena slagalici bit će permutacija koja indeksu mjesta (crni broj na slici 2) pridružuje indeks kvadratića koji se nalazi na danom mjestu (crveni broj na slici 2). Crveni brojevi (slika 2) su oni brojevi koji pišu na kvadratićima i koji putuju slagalicom pomicanjem kvadratića, crni brojevi sa slike označavaju mjesta, npr. neovisno o rasporedu kvadratića, crna jedinica je uvijek u lijevom gornjem uglu. Slagalici sa slike 2 bit će pridružena permutacija

Uočimo još da je takvo pridruživanje bijektivno, tj. za svaku pemutaciju iz S₁₆ postoji jedinstveni raspored kvadratića kojem je ta permutacija pridružena, te da je permutacija p parna (22 inverzije).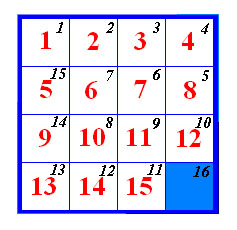

Slika 2

Već smo vidjeli da se slagalica može riješiti ako i samo ako se može riješiti parnim brojem pomaka, tj. zamjena praznog polja i kvadratića. To znači da ako se slagalica može riješiti, onda se permutacija p (koja je pridružena riješenoj slagalici) može dobiti iz permutacije r (koja je pridružena slagalici prije početka slaganja) komponiranjem s parnim brojem transpozicija. Kompozicija parnog broja transpozicija je parna permutacija pa odavde vidimo da permutacije p i r moraju biti iste parnosti. Kako je permutacija p parna, zaključujemo:

Lema 1. Ako je slagalici pridružena neparna permutacija, slagalica nije rješiva.

Slika 3

Ovime smo, relativno lako, uspjeli eliminirati polovicu slučajeva, točnije njih 15!/2 (jer promatramo slagalice s fiksiranim praznim poljem), ali nam ih je i preostalo još upravo toliko. Ako promotrimo slagalice sa slike 3 i slike 4, za prvu lako možemo zaključiti da nije rješiva (9 inverzija), ali o drugoj još ne možemo ništa reći jer ima paran broj inverzija (nula).

Slika 4

Iz prethodne leme vidimo zašto nitko nije uspio riješiti Loydov nagradni zadatak. Boss puzzle ima jednu inverziju premalo (ili previše), tj. ima ih 21 što je neparan broj pa takva slagalica nije rješiva.

Kao i prije, opet ćemo slagalici bijektivno pridruživati permutaciju, ali ovaj put iz S₁₅ (pridruživanje slagalici permutacije iz S₁₆ pokazalo se korisnim jer se odmah vidi da vrijedi lema 1, ali kako smo se prije ograničili samo na slagalice s fiksiranim praznim poljem kojih ima 15!, prirodnije je promatrati pemutacije iz S₁₅). Ponovno je riječ o permutaciji koja indekse mjesta preslikava u indekse kvadratića, ali ovaj put smo zanemarili prazno polje. Mjesta smo indeksirali kao na slici 5 pa bi slagalici s te slike bila pridružena permutacija

Permutacija r je parna (22 inverzije). Općenito vrijedi da će slagalici pridružena permutacija iz S₁₅ na prethodno definirani način biti iste parnosti kao i ona iz S₁₆. Tvrdnja je trivijalna čim uočimo da za permutaciju p iz S₁₆ koju smo prije pridruživali slagalici, zbog našeg početnog dogovora uvijek vrijedi p(16)=16 te da taj element nikako ne pridonosi broju inverzija permutacije p. U daljnjem ćemo tekstu pod pojmom permutacije koja je pridružena slagalici smatrati upravo definiranu permutaciju iz S₁₅.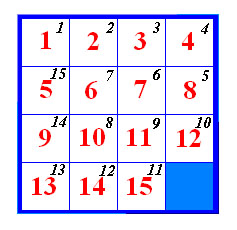

Slika 5

Kada bismo htjeli "posjetiti" sve indekse mjesta od 1 do 15 uzlaznim redoslijedom, to bismo mogli napraviti tako da se krećemo po zelenoj liniji sa slike 6. Svako polje proći ćemo točno jednom i opet se vratiti na početak, tj. na polje 1.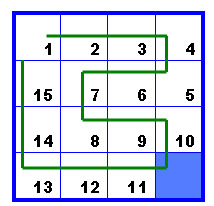

Slika 6

Definiramo poteze:

• prvi potez (s pomakom n) - pomak svih kvadratića u pozitivnom (negativnom) smjeru za n mjesta po zelenoj liniji sa slike 6;
• drugi potez - pomak svih kvadratića na mjestima 9, 10, 11 za jedno mjesto u pozitivnom (negativnom) smjeru.

Još ćemo zahtijevati da se nakon izvršenog poteza prazno polje opet nađe u desnom donjem uglu. To zapravo znači da će se onaj kvadratić koji smo prvi pomaknuli (prilikom provođenja drugog ili prvog poteza s pomakom 1) morati pomaknuti na kraju još jednom u odgovarajućem smjeru, tako da nam se prazno polje doista nađe na mjestu gdje ga i očekujemo. Pod pozitivnim smjerom misli se na smjer suprotan kazaljki na satu.

Malo objašnjenje prethodne definicije može se vidjeti na sljedećim slikama. Provođenje prvog poteza u negativnom smjeru s pomakom 1 prikazano je na slici 7, a provođenje drugog poteza u pozitivnom smjeru na slici 8. Potezi su provedeni na slagalici sa slike 1. Prvi potez s pomakom n isto je što i prvi potez s pomakom 1 proveden n puta.

Slika 7

Slika 8

Uočimo da prvi potez možemo poistovjetiti s ciklusom duljine 15, a drugi potez s ciklusom duljine 3. Permutacija koja će biti pridružena slagalici sa slike 7 upravo je ona koja se dobije komponiranjem ciklusa c i početne permutacije r, pri čemu je c = (5 9 13 14 15 12 11 10 6 7 8 4 3 2 1) (ovdje koristimo zapis ciklusa koji smo spomenuli u prvom poglavlju), tj. s = c◦r. Primijetimo još da su zapisi permutacije r (drugi redak) i permutacije c simetrični, u smislu da je prvi zrcalna slika drugoga. Da smo imali potez s pomakom 1 u pozitivnom smjeru, opet bismo imali s = c◦r, ali u tom slučaju bilo bi c = (1 2 3 4 8 7 6 10 11 12 15 14 13 9 5). Ako promotrimo zapis permutacije r, vidimo da su brojevi u drugom retku jednako razmješteni kao i u zapisu permutacije c. Slično zaključujemo i za drugu transformaciju, tj. slagalicu sa slike 8. Ako uzmemo d = (11 12 15), novodobivenoj slagalici bit će pridružena permutacija s = d◦r.

Prema tome, provođenjem poteza nad slagalicom dobivamo novu slagalicu kojoj je permutacija iste parnosti kao i permutacija slagalice koju smo imali na početku jer ciklusi c i d imaju neparan broj elemenata, što znači da su parni. Štoviše, vidimo da se provođenje poteza nad slagalicom svodi na komponiranje odgovarajućih permutacija.

Za kvadratiće s indeksima a i b na mjestima s indeksima c i d reći ćemo da su uzastopni ako su brojevi c i d uzastopni, tj. |c - d| = 1 ili ako je |c - d| = 14. Ako je c < d ili c = 15, a d = 1 te su a i b uzastopni, reći ćemo da je b iza a.

Za kvadratiće a, b, c reći ćemo da su uzastopni ako su a, b i a, c, ili b, a i b, c, ili c, a i c, b uzastopni.

Relacija "biti uzastopan" podudara se s našim intuitivnim shvaćanjem uzastopnosti s obzirom na zelenu liniju sa slike 6. Jednakošću |c - d| = 14 samo smo pokrili slučaj kada se jedan od kvadratića nalazi na mjestu 1, a drugi na mjestu 15. Primijetimo još da je relacija "biti uzastopan" simetrična: ako su a i b uzastopni, onda su i b i a uzastopni.

Ako promotrimo slagalicu sa slike 1, vidimo da su po našoj definiciji kvadratići s brojevima 3 i 4 te 1 i 5 uzastopni, ali kvadratići s brojevima 5 i 6 to nisu. Kvadratić 5 je na mjestu s indeksom 15, a kvadratić 6 na mjestu s indeksom 7. Također vidimo da je npr. kvadratić broj 4 iza kvadratića broj 3, kvadratić broj 15 iza kvadratića broj 12 (prazno polje zanemarujemo).

Ako iz S₁₅ odaberemo neku transpoziciju (a b), tada vrijedi (a b) = (b a) jer jedna i druga zamjenjuju elemente a i b, a ostale ostavljaju na miru. Ova digresija pokazat će se korisnom nakon sljedeće definicije.

Dvije transpozicije (a b) i (c d) zovemo susjednima ako je a = c te su kvadratići s brojevima a, b, d uzastopni.

Primijetimo da su (1 2) i (2 3) na slici 1 susjedne transpozicije. Također, (2 3) i (1 2) su susjedne jer je zbog prethodne napomene relacija "biti susjedan" simetrična. Transpozicije (1 2) i (2 6) na slici 1 nisu susjedne jer kvadratići s brojevima 1, 2, 6 nisu uzastopni.

Ako imamo kompoziciju dviju susjednih transpozicija (a b) i (a c), tada vrijedi (a c)◦(a b) = (a b c). Dakle, kompoziciju svakih dviju susjednih transpozicija možemo zapisati kao jedan ciklus duljine 3. Ova tvrdnja trebala bi nas motivirati za sljedeću lemu.

Lema 2. Svaka transpozicija može se zapisati kao kompozicija neparnog broja transpozicija tako da su svake dvije uzastopne transpozicije susjedne.

Ova tvrdnja uopće nije očita pa ćemo je dokazati. Bez smanjenja općenitosti možemo uzeti da je a < b. Ako je tako, promotrimo sljedeću jednakost:

Koje god dvije uzastopne transpozicije s desne strane uzmemo, vidimo da su one susjedne jer zamjenjuju uzastopne elemente. Nadalje, s desne strane imamo kompoziciju 2(b-a)-1, tj. neparnog broja transpozicija, pa naša tvrdnja vrijedi. Što smo točno ovdje radili, možemo ilustrirati jednim primjerom. Uzmimo a = 1, b = 4 te neka su između njih brojevi 2 i 3. Tada imamo

Prikažimo što smo dobili nakon pojedinog koraka, tj. nakon pojedinog komponiranja. Na početku imamo (1,2,3,4) i redom dobivamo

Dakle, pomicali smo jedinicu jedno po jedno mjesto udesno, a kad smo je zamijenili s četvorkom, četvorku smo pomicali jedno po jedno mjesto ulijevo sve dok se nije našla na mjestu na kojem je prije bila jedinica. Sada se napokon vidi da smo doista imali kompoziciju susjednih transpozicija.

Znamo da iz svake parne pemutacije možemo dobiti svaku parnu permutaciju komponiranjem prve s parnim brojem transpozicija. Kada bismo dokazali da se kompozicija dviju transpozicija može prikazati kao kompozicija parnog broja susjednih transpozicija, a već smo vidjeli da je kompozicija dviju susjednih transpozicija zapravo ciklus duljine 3, to bi značilo da se kompozicija dviju proizvoljnih transpozicija može prikazati kao kompozicija ciklusa duljine 3 oblika (a b c) za uzastopne kvadratiće a, b, c. Nadalje, ciklus duljine 3 nad uzastopnim kvadratićima odgovara upravo drugom potezu pa bi u tom slučaju bilo sasvim dovoljno pokazati da se ciklus duljine 3 nad uzastopnim kvadratićima uvijek može provesti. Time bismo dobili dovoljan uvjet rješivosti slagalice (nuždan uvjet već imamo).

Teorem. Kompozicija svakih dviju transpozicija (a b) i (c d) može se zapisati kao kompozicija ciklusa duljine 3 oblika (i  j  k) za uzastopne kvadratiće i, j, k.

Zbog potpunosti navodimo dokaz teorema iako on kvalitativno ne donosi ništa novo. Ideja dokaza sadržana je u dokazu leme 2.

Neka su brojevi a, b, c i d međusobno različiti. Možemo bez smanjenja općenitosti pretpostaviti da je a < b i c < d, ali i a < c jer smo pretpostavili da su sva četiri broja međusobno različita. Sada razlikujemo tri slučaja:

1. a < b < c < d,
2. a < c < b < d,
3. a < c < d < b.

Očito je (a b) ◦ (c d) = (a c) ◦ (a d) ◦ (a c) ◦ (a b).

1. slučaj: a < b < c < d.

Uzmimo prvo (a c) ◦ (a b). Kompoziciju tih dviju transpozicija provodimo na sljedeći način: prvo ćemo b pomicati jedno po jedno mjesto ulijevo sve dok ga ne zamijenimo s a, zatim a pomičemo jedno po jedno mjesto udesno sve dok ga ne zamijenimo s b-1 koji se nalazi na mjestu gdje se na početku nalazio b, nastavljamo pomicati a jedno po jedno mjesto udesno sve dok ga ne zamijenimo s c i konačno c pomičemo jedno po jedno mjesto ulijevo sve dok ga ne zamijenimo s b+1 koji se nalazi na mjestu na kojem je maloprije bio a. To možemo zapisati na sljedeći način:

S desne strane imamo ukupno (2(b-a)-1) + (2(c-b)-1) = (2(c-a)-1), dakle paran broj transpozicija. Možemo ih grupirati u zagrade tako da su u svakoj zagradi dvije uzastopne transpozicije koje su ujedno i susjedne. Svaku od tih zagrada možemo prikazati kao ciklus duljine 3 sastavljen od tri uzastopna kvadratića.

Uzmimo sada (a c) ◦ (a d). Uočimo da su nam prve dvije transpozicije poredale brojeve tako da je b ispred c, c ispred a, a ispred d pa iduće dvije transpozicije provodimo na nizu

Slično kao i kod (a c) ◦ (a b) ovdje imamo

S desne strane dobili smo (c-b) + (d-b-1) + (d-c-1) = 2(d-b-1) transpozicija, pri čemu su opet uzastopne transpozicije susjedne pa ih kao i prije grupiramo dvije po dvije u zagrade. Svaka zagrada može se zapisati kao ciklus duljine 3 nad uzastopnim kvadratićima.

Napokon zaključujemo da se za a < b < c < d kompozicija transpozicija (a b) i (c d) može zapisati kao kompozicija ciklusa duljine 3 nad uzastopnim kvadratićima.

2. slučaj: a < c < b < d.

Opet ćemo, kao u prethodnom slučaju, promatrati kompoziciju prvih dviju transpozicija s desne strane pa potom i kompoziciju drugih dviju transpozicija s desne strane. Uzmimo prvo (a c) ◦ (a b). Prvo ćemo b pomicati jedno po jedno mjesto ulijevo sve dok ga ne zamijenimo s a, zatim a pomičemo jedno po jedno mjesto udesno sve dok ga ne zamijenimo sa c - 1 i konačno c pomičemo jedno po jedno mjesto udesno sve dok ga ne zamijenimo s b - 1. Imamo

S desne strane dobili smo (b-a) + (c-a-1) + (b-c-1) = 2(b-a-1) transpozicija. Svake dvije uzastopne transpozicije su susjedne pa se ponovi postupak iz 1. slučaja.

Promatramo (a c) ◦ (a,d). Prve dvije transpozicije razmjestile su nam brojeve tako da je sada b ispred a, a ispred c, c ispred d, tj. imamo niz

Zbog toga se (a c) ◦ (a d) dobije kao kompozicija parnog broja susjednih transpozicija kao što smo dobili i (a c) ◦ (a b).

3. slučaj: a < c < d < b.

Kompoziciju transpozicija (a c) ◦ (a b) provodimo na sljedeći način: pomičemo c jedno po jedno mjesto udesno sve dok ga ne zamijenimo s b, zatim b pomičemo jedno po jedno mjesto ulijevo sve dok ga ne zamijenimo s a, zatim pomičemo a jedno po jedno mjesto udesno sve dok se ne nađe na istom mjestu na kojem se na početku nalazio c, tj.

Opet imamo paran broj susjednih transpozicija, tj. s desne strane imamo točno (b-c) + (b-a-1) + (c-a-1) = 2(b-a-1) transpozicija. Svake dvije uzastopne transpozicije, jer su susjedne, možemo zapisati kao ciklus duljine 3 na susjednim kvadratićima.

Sada nam je b ispred a, a ispred d i d ispred c, tj. imamo sljedeći niz:

Kompoziciju (a c) ◦ (a d) prikazat ćemo kao kompoziciju parnog broja susjednih transpozicija kao što smo prikazali i (a c) ◦ (a,b) u 1. slučaju - jednostavno se zamijene odgovarajuća slova.

Preostala nam je još mogućnost da brojevi a, b, c, d nisu međusobno različiti. Među njima sigurno postoje tri međusobno različita broja a < b < c jer kada bi dva i dva broja bila ista, tada bi kompozicija bila identiteta. Imamo šest mogućih slučaja:

1. (b c) ◦ (a b) = (a b-1) ◦ … ◦ (a a+1) ◦ (c a) ◦ … ◦ (c c-1) ◦ (b c) ◦ … ◦ (b+1 b),
2. (b c) ◦ (a c) = (c b+1) ◦ … ◦ (c c-1) ◦ (a c) ◦ … ◦ (a a+1) ◦ (b a) ◦ … ◦ (b b-1),
3. (a c) ◦ (a b) = (b c) ◦ (a c),
4. (a b) ◦ (b c) = (b c) ◦ (a c),
5. (a c) ◦ (b c) = (b c) ◦ (a b),
6. (a b) ◦ (a c) = (b c) ◦ (a b).

U svakom od njih lijevu smo stranu uspjeli zapisati kao kompoziciju susjednih transpozicija. Lako se provjeri da je desna strana kompozicija parnog broja transpozicija pa je možemo zapisati kao kompoziciju ciklusa duljine 3 nad uzastopnim kvadratićima.

Time je teorem dokazan jer smo ispitali sve moguće slučaje.

Lema 3. Nad tri uzastopna kvadratića možemo provesti oba ciklusa duljine 3.

Primjerom ćemo pokazati kako se spomenuti ciklusi mogu provesti. Uočimo prvo da postoje samo dva zanimljiva ciklusa duljine 3, a onaj treći, identiteta, sigurno zadovoljava tvrdnju.

Uzmimo slagalicu sa slike 9 i odaberimo brojeve 1, 2, 3. Pokazat ćemo da je na njima moguće provesti jedan paran ciklus duljine 3, tj. da je slagalicu moguće dovesti u položaj sa slike 12.

Slika 9

Prvo se provede prvi potez s pomakom 7 u pozitivnom smjeru (slika 10).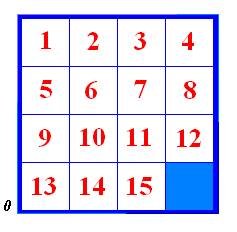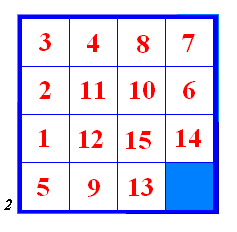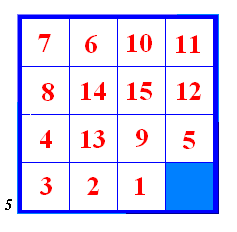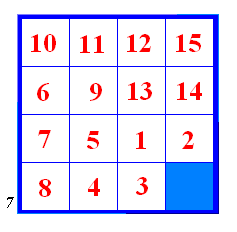

Slika 10

Zatim provedemo drugi potez u pozitivnom smjeru (slika 11).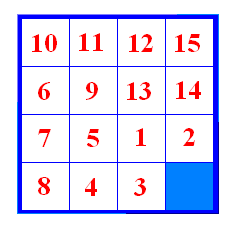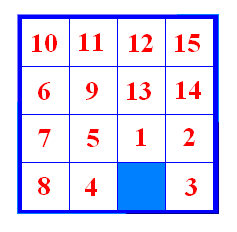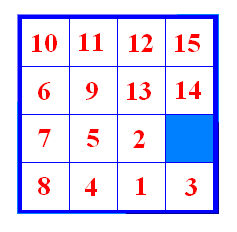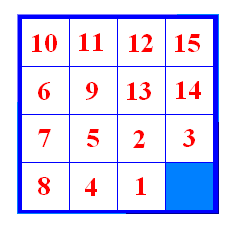

Slika 11

Ponovimo prvi potez s pomakom 7, ali sada u negativnom smjeru (slika 12).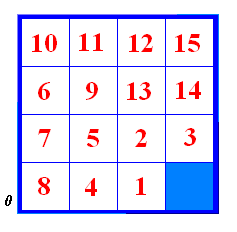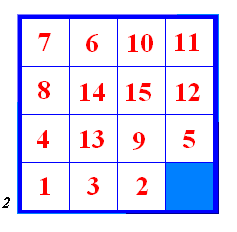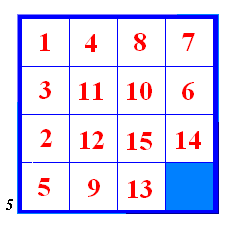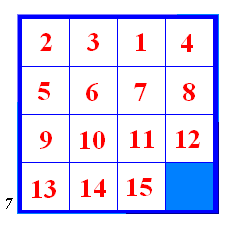

Slika 12

Analogno se može provesti i onaj drugi ciklus duljine 3 na tim istim brojevima.

Napokon, zaključujemo da je slagalica rješiva ako i samo ako je njoj pridružena permutacija parna. Štoviše, slagalica je rješiva ako i samo ako je rješiva potezima koje smo prethodno definirali. U idućem poglavlju vidjet ćemo i kako je možemo riješiti.

4. Metoda rješavanja

U ovom ćemo poglavlju opisati jednu metodu za rješavanje slagalice. Pritom ćemo koristiti samo poteze koje smo prije definirali. Prednost ove metode je to što ne ovisi o rasporedu kvadratića na slagalici. Ako je slagalica rješiva, provođenjem idućeg postupka slagalica će biti riješena. Ako nije, dobit ćemo Loydovu slagalicu s početka teksta. Naravno, algoritam koji smo konstruirali ne mora biti i najbrži, štoviše on to vjerojatno i nije. Radi se samo o jednom primjeru koji ilustrira način razmišljanja kojim smo došli do uvjeta za rješivost slagalice.

Za početak fiksirajmo jedan broj, tj. kvadratić. Zbog određenosti uzmimo da je to broj 1, iako bi i svaki drugi bio jednako dobar. Kada bismo putovali po zelenoj liniji sa slike 6, krenuvši od broja 1, u negativnom smjeru, indekse mjesta posjetili bismo sljedećim redoslijedom:

Postupak se sastoji u tome da, provodeći ranije definirane poteze, dovedemo kvadratić s brojem 2 iza kvadratića s brojem 1, kvadratić s brojem 3 iza kvadratića s brojem 2, kvadratić s brojem 4 iza kvadratića s brojem 3, kvadratić s brojem 8 iza kvadratića s brojem 4…

Ako smo 12 puta ponovili postupak, tj. doveli kvadratić 13 iza kvadratića 14, slagalica je, ako je rješiva, riješena. Naime, iz prethodno dokazanih tvrdnji znamo da će se tada iza kvadratića s brojem 13 naći kvadratić s brojem 9, a ne onaj brojem 5 (zašto?).

Sada ćemo kao primjer provesti algoritam na slagalici sa slike 13.

Slika 13

Fiksirat ćemo kvadrat s brojem 5. Primijetimo da je iza njega kvadrat s brojem 1 koji bi se u riješenoj slagalici i trebao nalaziti iza njega. Sada želimo kvadrat s brojem 2 dovesti iza kvadrata s brojem 1. Najprije provedemo prvi potez u negativnom smjeru s pomakom 2, a potom drugi potez u negativnom smjeru. Postupak je proveden na slici 14.

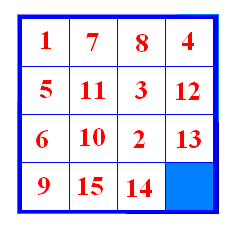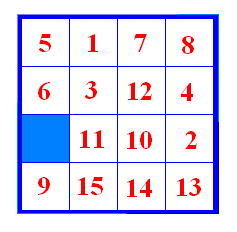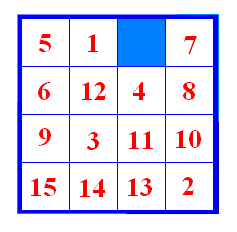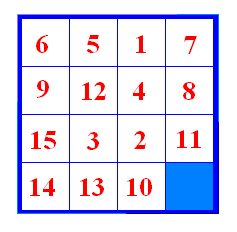
Slika 14

Sada provedemo prvi potez s pomakom 2 u negativnom smjeru, zatim drugi potez u negativnom smjeru (slika 15).

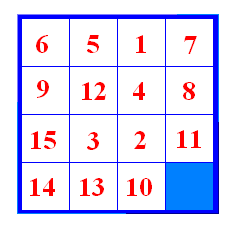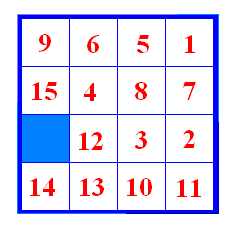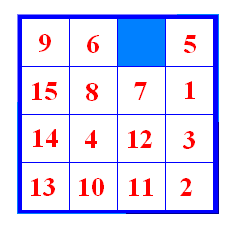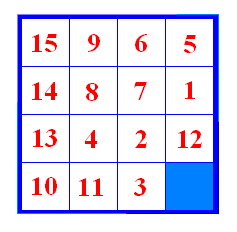
Slika 15

Nastavljamo s prvim potezom s pomakom 2 u negativnom smjeru, drugim potezom u negativnom smjeru, prvim potezom s pomakom 1 u negativnom smjeru, drugim potezom u pozitivnom smjeru (slika 16).

Slika 16

Sada ćemo dovesti kvadratić s brojem 3 iza kvadratića s brojem 2. Prvo slijedi prvi potez u pozitivnom smjeru s pomakom 3, a zatim drugi potez u negativnom smjeru (slika 17).

Slika 17

Sada slijedi prvi potez u negativnom smjeru za pomak 2, drugi potez u negativnom smjeru (slika 18).

Slika 18

Sljedeći potez bio bi dovesti kvadratić s brojem 4 iza kvadratića s brojem 3, no ostale poteze koje treba provesti samo ćemo zapisati u sljedeću tablicu. U tablici slovo p predstavlja pozitivan, a n negativan smjer. Ono što smo naposlijetku dobili jest upravo slika Loydove slagalice s početka teksta, za koju znamo da nije rješiva. Naravno, kad bismo išli brojati inverzije permutaciji pridruženoj slagalici sa slike 13, vidjeli bismo da ih zaista ima neparan broj.

5. Komentar

Za kraj uočimo nekoliko pojedinosti. Prilikom ispitivanja rješivosti slagalice definirali smo na koji ćemo način slagalici pridruživati permutaciju iz S₁₅. Nakon toga smo dokazivali neke tvrdnje vezane uz rješivost slagalice koje uopće nisu ovisile o načinu na koji smo konstruirali spomenutu permutaciju. Jedino što je bilo bitno jest da se radi o nekakvoj permutaciji koja djeluje na skupu koji ima onoliko elemenata koliko slagalica ima kvadratića te da na tom skupu imamo totalni uređaj kako bismo mogli uvesti relaciju "biti uzastopan" na skupu kvadratića. Odavde vidimo da smo slagalici mogli pridruživati permutaciju na neki drugi način, npr. mogli smo uzeti takvo pridruživanje koje će riješenoj slagalici pridruživati identitetu. Na kraju bismo došli do istog zaključka.

Ako imamo neku nerješivu slagalicu, tada provođenjem jedne transpozicije nad bilo kojima dvama kvadratićima (npr. uspijemo nekako izokrenuti devetku i šesticu) dobivamo rješivu slagalicu. Dakle, ako Loydovoj Boss puzzle slagalici nekako zamijenimo jedinicu i dvojku ili bilo koja druga dva kvadratića, dobivamo slagalicu koja je rješiva. Slično, zamjenom nekih dvaju kvadratića na rješivoj slagalici dobivamo nerješivu slagalicu koja se metodom opisanom u četvrtom poglavlju može svesti na Loydovu Boss puzzle slagalicu. Znači, svaka slagalica se ili može riješiti ili joj se kvadratići mogu složiti kao u Loydovoj slagalici.

Čitav članak bio je posvećen rješavanju slagalice 4×4, ali broj 4 gotovo nigdje nismo spominjali. Kada bismo uzeli sličnu slagalicu, ali sada 5×5 ili 20×30, i htjeli naći nužne i dovoljne uvjete njezine rješivosti, skoro da bismo mogli prepisati isti dokaz samo što bi nam se promatrane permutacije nalazile u S₂₄, odnosno u S₅₉₉. Naravno, pridruživanje permutacije slagalici proveli bismo na drugačiji način te bismo u posljednjem koraku drugačije pokazali kako se može provesti ciklus duljine 3 (ako se može provesti).

Dakle, dobili smo nešto općenitiji rezultat koji možemo primijeniti na neku veću ili manju slagalicu. Uzimanjem u obzir prethodnih napomena mogu se riješiti sljedeći zadaci.

6. Zadaci

1. Mogu li se kvadratići iz slagalice sa slike 19 složiti kao na slagalici sa slike 20?
   
   
   Slika 19
   
   
2. Isto pitanje, ali uz uvjet da ne mičemo jedinicu iz lijevog gornjeg ugla.
   
   
   Slika 20
   
   
3. Mogu li se brojevi na slagalici sa slike 19 rasporediti po kvadratićima tako da se slagalica ne može riješiti, tj. dovesti u položaj sa slike 20?
   
   
4. Definirajte pridruživanje permutacije slagalici 3×3. Što bi bili uzastopni kvadratići? Kako bi proveli ciklus duljine 3 nad uzastopnim kvadratićima? Kada je slagalica rješiva?
   
   
5. Mogu li se kvadratići na slagalici sa slike 21 složiti tako da se dobije magični kvadrat (pri čemu praznom polju pridružimo vrijednost 6)?
   
   
   Slika 21
   
   
6. Na koliko načina možemo brojeve 4, 7, 10, 13 napisati na prazne kvadratiće slagalice sa slike 22 tako da se ona ne može riješiti? Ovisi li taj broj načina o poziciji izbrisanih kvadratića, njihovom broju ili o brojevima koje smo izbrisali?
   
   
   Slika 22
   
   
7. Što možete reći o rješivosti slagalice n×n s dvama praznim poljima? Slagalicu smatramo riješenom ako se u i-tom retku i j-tom stupcu nalazi kvadratić (i-1)·n + j, a na zadnjim dvama mjestima u posljednjem retku prazna polja.

Literatura

1. Uvod
2. Permutacije
3. Ispitivanje rješivosti slagalice
4. Metoda rješavanja
5. Komentar
6. Zadaci
Literatura