
| Dokazi i primjene AG nejednakosti |  |  |
|
Sadržaj: 1. Aritmetičko-geometrijska nejednakostNejednakost između aritmetičke i geometrijske sredine, ili kraće AG nejednakost, svakako je jedna od najpoznatijih algebarskih nejednakosti. Radi se o usporedbi aritmetičke sredine
i geometrijske sredine
pri čemu su a = (a1,...,an) i w = (w1,...,wn) uređene n-torke pozitivnih brojeva i Wn = w1+...+wn.
U literaturi se mogu naći deseci različitih dokaza ove nejednakosti, a mi ćemo promotriti razne vizualne dokaze AG nejednakosti za n = 2 s jednakim težinama, tj. razmotrit ćemo dokaze nejednakosti
koja vrijedi za svaka dva pozitivna realna broja a i b. Jednakost se postiže ako i samo ako je a = b. 2. Dokazi AG nejednakostiPrvo promotrimo algebarski dokaz nejednakosti (1). Za svaka dva pozitivna broja a i b očito vrijedi nejednakost (√a − √b)2 ≥ 0, pri čemu jednakost vrijedi ako i samo ako je a = b. Kvadriranjem binoma i daljnjim transformacijama dobivamo a + b ≥ 2√ab, tj.
Promotrimo sada nekoliko geometrijskih dokaza nejednakosti (1). Dokaz 1. 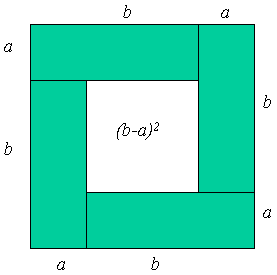 Slika 1. Veći kvadrat ima stranicu duljine a + b i njegova je površina očito veća od površine četiriju pravokutnika sa stranicama a i b (vidjeti sliku 1). Dakle, imamo a + b ≥ 2√ab, odakle slijedi nejednakost (1). Jednakost se postiže ako i samo ako je površina velikog kvadrata jednaka površini četiriju pravokutnika, odnosno ako i samo ako kvadrat u sredini figure iščezava, a to se događa ako i samo ako je b − a = 0. Dokaz 2. 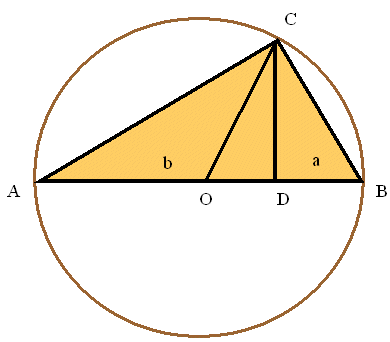 Slika 2. U pravokutnom trokutu ABC s hipotenuzom AB visina CD dijeli hipotenuzu na odsječke BD i DA duljina a i b (slika 2). Prema Euklidovu poučku, duljina visine na hipotenuzu jednaka je geometrijskoj sredini njenih duljina odsječaka na hipotenuzi, tj. |CD| = √ab. S druge strane, polumjer kružnice opisane pravokutnom trokutu ABC jednak je polovini duljine hipotenuze, tj.
Budući da je u pravokutnom trokutu COD hipotenuza CO dulja od katete CD, slijedi nejednakost (1). Jednakost se postiže ako i samo ako trokut COD degenerira u dužinu CD, tj. ako i samo ako se težišnica CO podudara s visinom CD. To se događa ako i samo ako je trokut ABC jednakokračan, odnosno ako i samo ako su odsječci visine na hipotenuzi jednake duljine a = b. Dokaz 3.  Slika 3. Kvadrat ABCD ima stranicu duljine √a, a pravokutnik ABFE ima stranice duljina √a i √b, b ≤ a. Sad imamo
Time je ponovno dokazana AG nejednakost (1). Dokaz 4. 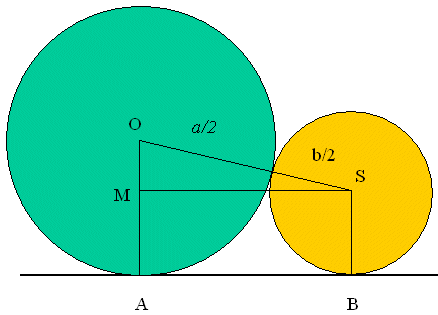 Slika 4. Neka su dane kružnice središta O i S te polumjera a/2 i b/2, a ≥ b, koje se diraju izvana, te neka je AB zajednička vanjska tangenta tih dviju kružnica. Točke A i B su dirališta tangente i kružnica. Trapez ABSO ima dva prava kuta pri vrhovima A i B. Neka je dužina SM paralelna s AB. Tada je trokut OMS pravokutan. Hipotenuza OS ima duljinu (a + b)/2, a kateta OM ima duljinu (a − b)/2. Prema Pitagorinu poučku imamo
Budući da je u pravokutnom trokutu hipotenuza dulja od katete, slijedi valjanost nejednakosti (1). Dokaz 5. 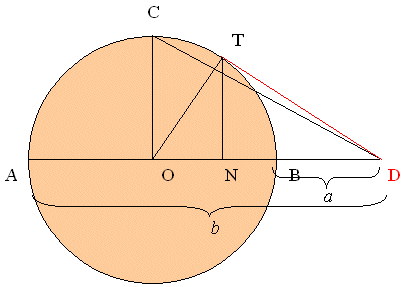 Slika 5. Neka je dana kružnica s promjerom AB duljine b − a i središtem O. Točka D nalazi se na pravcu kroz A i B tako da je |AD| = b i točka B je između točaka A i D. Tada je |BD| = a. Iz točke D povučena je tangenta na kružnicu. Točka T je diralište te tangente i kružnice. U pravokutnom trokutu OTD hipotenuza ima duljinu |OD| = (a+b)/2, a duljinu katete TD možemo izračunati pomoću Pitagorina poučka:
Budući da je hipotenuza dulja od katete, vrijedi AG nejednakost (1).
Inače, na ovoj slici pojavljuje se nejednakost još dviju sredina: kvadratne i harmonijske. Naime, ako je CO polumjer okomit na promjer AB, tada duljina hipotenuze CD iznosi
Ovaj se izraz naziva kvadratnom sredinom brojeva a i b. Nadalje, ako je N nožište visine iz vrha T u pravokutnom trokutu OTD, tada iz sličnosti trokuta TND i OTD slijedi |ND| : |TD| = |TD| : |OD|, tj.
Ovaj se izraz naziva harmonijskom sredinom brojeva a i b. Iz slike 5 očitavamo da je |ND| < |TD| < |OD| < |CD|, tj. sredine rastu ovim slijedom: harmonijska, geometrijska, aritmetička i kvadratna. Ova se činjenica generalizira na sredine definirane pomoću opće potencije, ali to prelazi okvire ovog rada. Sljedeća dva dokaza pripadaju grupi tzv. analitičkih dokaza AG nejednakosti. Dokaz 6. 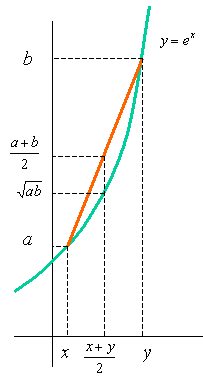 Slika 6. Funkcija f(x) = ex je konveksna, što geometrijski znači da je graf funkcije između dviju točaka na grafu uvijek ispod tetive koja spaja te dvije točke. Na grafu eksponencijalne funkcije odaberimo dvije točke s koordinatama (x,ex) i (y,ey) te uvedimo oznake a = ex i b = ey. Pravac kroz odabrane točke ima jednadžbu
pa točka na tom pravcu s apscisom (x + y)/2 ima ordinatu (a + b)/2. S druge strane, točka s istom apscisom, ali na grafu eksponencijalne funkcije ima ordinatu e(x + y)/2, što nakon sređivanja postaje √ab. Budući da se točka na grafu nalazi ispod točke na tetivi, slijedi AG nejednakost
Dokaz 7. 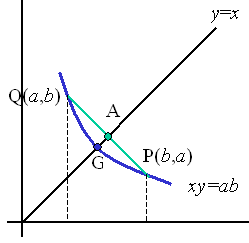 Slika 7. Promotrimo hiperbolu x·y = ab. Točke P(b,a) i Q(a,b) pripadaju toj hiperboli. Pravac koji prolazi kroz te dvije točke ima jednadžbu Promotrimo sad presjek hiperbole i tetive PQ s pravcem y = x. Na hiperboli je presjek točka G s koordinatama a na tetivi točka A s koordinatama
Budući da je točka G ispod točke A (zbog konveksnosti funkcije čija je hiperbola graf), slijedi AG nejednakost. 3. Primjene AG nejednakostiAG nejednakost je snažno sredstvo za dokazivanje raznih složenijih nejednakosti i u literaturi se mogu naći brojni zadaci koji se svode na upotrebu ove nejednakosti. U sljedećih nekoliko primjera pokazat ćemo neke primjene opće AG nejednakosti. Primjer 1: Maksimum polinoma. Ako je L površina sferne kapice danog polumjera R i V volumen odgovarajućeg sfernog odsječka, tada vrijedi 18πV2 ≤ L3, pri čemu jednakost vrijedi ako i samo ako je riječ o polusferi. Dokaz. Koristeći poznate formule za površinu sferne kapice L = 2πRh i volumen sfernog odsječka V = πh2(3R−h)/3 dobivamo omjer
Nađimo maksimum polinoma h (3R−h)2 za h ∈ [0,R]. Napišimo AG nejednakost za tri broja C1h, C2(3R−h) i C2(3R−h), pri čemu su C1 i C2 neodređeni koeficijenti:
Koeficijente C1 i C2 odredimo tako da u aritmetičkoj sredini na desnoj strani nejednakosti nestane varijabla h. Dobivena konstanta na desnoj strani bit će maksimum polinoma na lijevoj strani ako postoji h0 za koji se postiže jednakost. Varijabla h nestat će ako vrijedi C1−2C2 = 0. Bez smanjenja općenitosti uzmimo da je C1 = 2 i C2 = 1. Jednakost u AG nejednakosti postiže se ako su brojevi jednaki, tj. ako vrijedi C1h = C2(3R−h), odakle dobivamo da je h0 = R. Uvrštavanjem koeficijenata C1 i C2 u AG nejednakost dobivamo 2h(3R−h)2 ≤ 8R3, tj. h(3R−h)2 ≤ 4R3. Dakle, vrijedi
Jednakost se postiže ako i samo ako je visina kapice jednaka polumjeru (tj. kapica je u stvari polusfera). Ova metoda s uvođenjem neodređenih koeficijenata i korištenjem AG nejednakosti može se generalizirati za opću situaciju određivanja maksimuma polinoma koji je dan u obliku produkta. Primjer 2: Limes.
Dokaz. Pretpostavimo da je n ≥ 3. Tada koristeći AG nejednakost za n brojeva 1, n1/n, n2/n, …, n(n−1)/n imamo
Budući da n-1/3 teži k 0 kada n teži u beskonačnost, slijedi da tada i n1/n − 1 teži k 0. Primjer 3: Hölderova nejednakost. Neka su a i b dvije n-torke pozitivnih realnih brojeva te neka su p i q dva pozitivna broja takva da je 1/p + 1/q = 1. Tada vrijedi
Dokaz. Gornja nejednakost može se napisati u obliku
a ta se nejednakost dokazuje koristeći težinsku AG nejednakost za dva broja:
1. Aritmetičko-geometrijska nejednakost | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
